Расчёт параметров модели и переходной характеристики

2.   Расчёт параметров модели и переходной характеристики

В соответствии с заданием для данного канала требуется рассчитать переходной процесс по ЭДС якоря eя при сбросе напряжения на  якорной обмотке uя  до нулевого значения UяN .

При этом все остальные величины равны номинальным значениям в исходном состоянии.

Поскольку

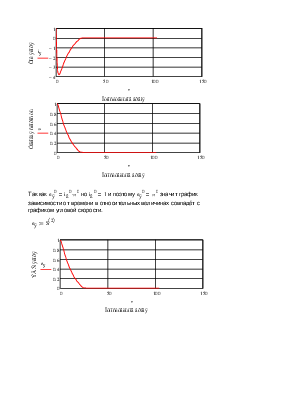
Так как

то уравнение

не требуется в данном случае

Следовательно мат. модель будет ввиде 2-х уравнений

Начальные условия

Расчитываем параметры математической модели. Введём исходные (паспортные данные) ДПТ НВ

- Мощность

- Скорость

- Момент

- Напряжение якоря

- Ток якоря

- Сопротивление якоря

- Индукция якоря

-Пост. врем. якоря

 - Ток возб.

- Напряжение возбуждения

- Сопрот. возб.

- Индукт. возб.

- Пост. врем. возб.

- Пост. электр.

- Момент инерц. якоря

- Пост. магн. потока

- Электромех. пост. времени

- ЭДС якоря

Так как

В результате расчётов получим следующие величины параметров

Запишем мат. модель с найденными параметрами

Выберем интервал и шаг рассчёта

Определение функции sign

Определение функции-матрицы правых частей уравнения

- Ток якоря

- Угловая скорость

Задание интервала и шага расчёта

Задание начальных условий

Расчёт

Перенос результатов в матрицы столбцы

Так как  но  и поэтому  значит график зависимости от времени в относительных величинах совпадёт с графиком угловой скорости.

3.  Анализ полученных результатов

Анализ проводим при набросе напряжения на якорной обмотке от нуля до номинального значения.

В начальный момент времени величины имеют следующие значения:

Так как переходной процесс расчитывается при набросе напряжения на обмотке возбуждения Uв , то по завершении переходного процесса все величины будут равны их номинальным значениям:

Полученны в результате анализа начальные значения соответствуют расчётным в переходном процессе.

Определим характер переходного процесса:

Полученная в п.2 математическая модельнелинейна из-за произведений   и функции . Линеаризуем её с помощью приближённых замен

Подставим замену  и получим характеристическое уравнение: 

Так как корни вещественные, то переходные процессы имеют апериодический характер, что мы и видим в результате расчётов.