Модель АРПСС - прогноз об инвестициях в основной капитал России, страница 2

Анализ настоящих данных лучше всего провести с использованием пакета STATISTICA 7.0 в модуле “Временные ряды и прогнозирование” (Time Series/Forecasting), т.к. размещенная в таблице числовая информация представляет собой временной ряд – совокупность последовательных измерений показателя, произведенных через одинаковые интервалы времени. Воспользуемся таким методом прогнозирования как ARIMA.

В рамках дальнейшего анализа, прежде всего, необходимо визуально оценить поведение точек на графике временного ряда, который выглядит следующим образом:

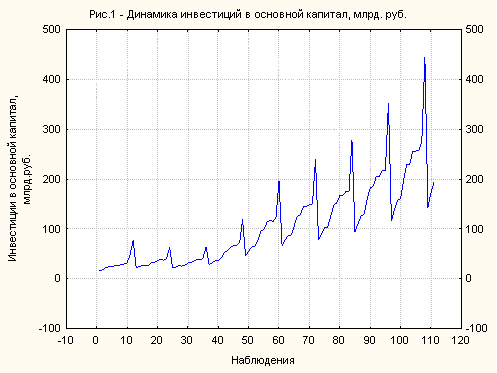
Из графика отчетливо видно, что динамика инвестиций в основной капитал имеет возрастающий тренд, а также сезонную составляющую. Поэтому для целей дальнейшего анализа имеет смысл преобразовать исходный временной ряд в стационарные данные, для которых среднее значение является постоянной величиной, а выборочные дисперсия и автокорреляция не меняются во времени.

Однако прежде чем преобразовать исходный ряд в стационарные данные оценим сезонную составляющую, изображенную на следующем графике:

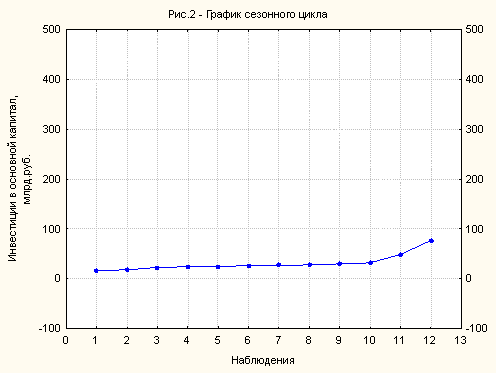
С помощью этого графика можно непосредственно определить характер сезонности. Так, в течение первых девяти месяцев объемы инвестиций в основной капитал колеблются вокруг примерно одного и того же уровня. Однако, начиная с октября, наблюдается устойчивый рост рассматриваемого показателя, пик которого приходится на декабрь. В принципе, это объясняется тем, что финансовый результат любого предприятия определяется именно по итогам финансового года, который в свою очередь совпадает с календарным годом. Финансовый результат существует в двух формах: в форме прибыли или убытка. В случае, если организация получает прибыль, то, как правило, она направляет значительную ее часть в виде капитальных вложений на обновление основных фондов. Тогда как в остальные месяцы года предприятие планирует осуществлять амортизационные взносы равными долями на каждый квартал, что и обусловливает колебание инвестиций с января по октябрь примерно на одном и том же уровне.

После взятия четырех разностей, одна из которых была с 1 лагом, а три других – с лагом, равным 12, был получен стационарный ряд капитальных вложений, изображенный на рис.3:

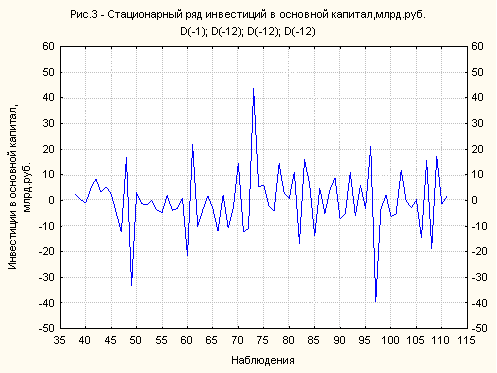
Далее целесообразно решить, какой тип модели будет подобран к полученным данным, и какое количество параметров присутствует в модели, иными словами, нужно идентифицировать модель АРПСС. Основными инструментами идентификации в данном случае выступают графики, а также автокорреляционная функция (АКФ) и частная автокорреляционная функция (ЧАКФ). Это решение не является простым и, как правило, требуется основательно поэкспериментировать с альтернативными моделями.

Автокорреляционную функцию отражает следующий график:

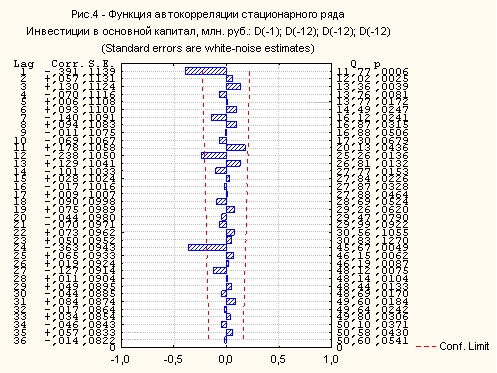
Частная автокорреляция имеет следующий вид:

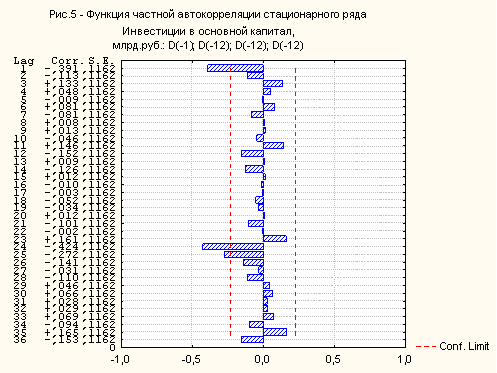
Таким образом, видно, что обе функции обрываются на первом лаге, поэтому для целей дальнейшего анализа можно применить любую модель АРПСС. Методом ручной подгонки зададим параметры q = 1 и Qs = 2, т.е. в основу будущего прогноза положим авторегрессионную модель со скользящим средним, причем с сезонными данными: (1;1;0)(0;3;2). Просмотрим результаты АРПСС:

Таблица 2 - Таблица результатов АРПСС
Параметр	Значение параметра	Асимпт. Ст. ошиб.	Асимпт. t (56)	p	Нижняя 95% дов.	Верхняя 95% дов.
p(1)	-0,362840	0,111407	-3,256896E+00	0,001729	-0,584979	-0,140701
Qs(1)	0,510968	0,000000	1,072874E+10	0,000000	0,510968	0,510968
Qs(2)	0,488996	0,000000	1,072874E+10	0,000000	0,488996	0,488996