Создание базовой модели схемы замещения электрической цепи

4ОПИСАНИЕ ДОКУМЕНТА MATHCAD

Создадим базовую модель для решения системы дифференциальных уравнений 5-го порядка при помощи символьных вычислений

   (1)              

   (2)            

Далее необходимо выразить неизвестные dILи dUCиз вышеуказанных дифференциальных уравнений

Задаём начальные условия IL=0, UC=0, и записываем вектор производных V

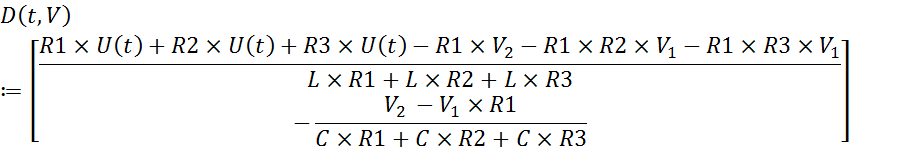
Для решения дифференциальных уравнений с начальными условиями используем rkfixed–функция для решения ОДУ и систем ОДУ методом Рунге-Кутта.

При решении дифференциального уравнения создаём вектор начальных условий из двух элементов V, который затем используется при формировании вектора-функции правой части дифференциального уравнения. При обращении к функции rkfixedуказывается имя вектора V, границы интервала, на котором ищется решение уравнения (0 0,0079), количество точек, в которых ищется решение (1000), вектор-функция, описывающая правую часть дифференциального уравнения (D).

Матрица, полученная в результате решения, содержит три столбца: первый столбец содержит значения T, в которых ищется решение; второй столбец содержит значения напряжения UC; и третий значения тока IL.

По закону Ома определяем общее сопротивление и общий ток в цепи путём создания функции от дискретной переменной t. На одном графике строим функции общего тока, рассчитанные по законам Ома и Кирхгофа (Приложение А, рисунок 5).

Экспериментально определяем максимальное значение тока для различных частот и из полученных данных составляем вектор свободных коэффициентов (Приложение А).

Находим аппроксимирующую функцию.

Определяем набор функции:

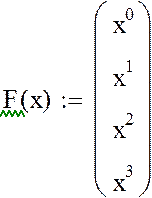
                  Определяем коэффициенты регрессии:

Исследуем влияние частоты на амплитуду силы тока и проведём аппроксимацию полученной зависимости при помощи линейной регрессии общего вида (Приложение А, рисунок 6).

5 ВЫВОДПО РЕЗУЛЬТАТАМ ИССЛЕДОВАНИЙ

        В результате проведенной работы мы создали базовую модель схемы замещения электрической цепи.

        В пакете MathCAD по полученной математической модели, используя функцию rkfixed,  определили значения функций напряжения, ЭДС, и силы тока по закону Кирхгофа и построили графики функции силы тока на конденсаторе, которая изменяется по синусоидальному закону.

Затем рассчитали общее сопротивление цепи и общий ток по закону Ома и сравнили полученные значения с рассчитанными раньше, в результате функции общего  синусоидального тока,  практически совпали, что видно на графике .

Также определили значения резонансной частоты и  исследовали влияние изменение амплитуды силы тока в зависимости от частоты, подставляя в формулу функции значения изменяемого параметра w и построили график амплитудно-частотной характеристики.

Можно сделать вывод, что с увеличением частоты амплитуда силы тока увеличивается, достигает своего максимума при резонансной частоте w=1628 рад/с, а затем начинает  уменьшаться.