Особенностью предлагаемого излучателя является возможность изменения потока излучения ИП путем создания разных по излучающей способности частей поверхности.
Пусть
одна из частей поверхности имеет коэффициент излучения ![]() ,а
другая
,а
другая ![]() , а температура тела неизменна.
, а температура тела неизменна.
Известно, что энергетическая светимость тела определяется по закону Стефана-Больцмана (4).
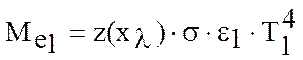
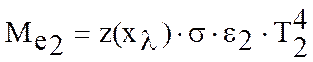
Тогда
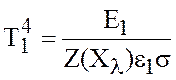
Энергетическую светимость
для ИП с коэффициентом ![]() при неизменной температуре
выразим как:
при неизменной температуре
выразим как:
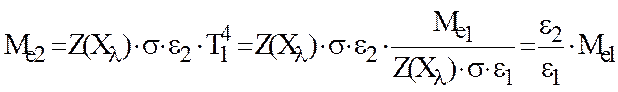
Тогда
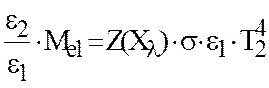
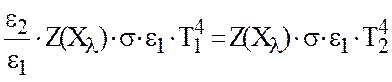
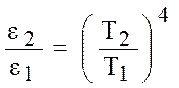 (5)
(5)
Как следует из выражения
(4), если заданы температурные точки калибровки, то, определив необходимое
отношение коэффициентов излучения ![]() /
/![]() и подобрав материал излучающей
поверхности или ее обработку, можно реализовать заданные точки калибровки.
и подобрав материал излучающей
поверхности или ее обработку, можно реализовать заданные точки калибровки.
Построим
графики зависимости отношения температур Т2/Т1 от отношения
коэффициентов излучения ![]() /
/![]() . Для различных материалов отношение
. Для различных материалов отношение ![]() /
/![]() имеет
различный порядок. Поэтому для построения зависимости возьмем два ряда данных:
имеет
различный порядок. Поэтому для построения зависимости возьмем два ряда данных: 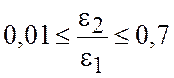 (рис. 3.1) и
(рис. 3.1) и 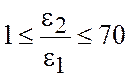 (рис. 3.2). Исходные данные
приведены в таблицах 3.1 и 3.2.
(рис. 3.2). Исходные данные
приведены в таблицах 3.1 и 3.2.
Таблица 3.1
|
ε2/ε1 |
0,02 |
0,03 |
0,04 |
0,05 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
|
Т2/Т1 |
0,376 |
0,416 |
0,447 |
0,473 |
0,562 |
0,669 |
0,740 |
0,795 |
0,841 |
0,880 |
0,915 |
Таблица 3.2
|
ε2/ε1 |
2 |
3 |
4 |
5 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
|
Т2 / Т1 |
1,19 |
1,32 |
1,41 |
1,49 |
1,78 |
2,11 |
2,34 |
2,51 |
2,66 |
2,78 |
2,89 |
Рисунок
3.1 Зависимость Т2/Т1 = f (ε2/ε1) при 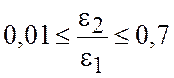
 Рисунок 3.2. Зависимость Т2/Т1
= f (ε2/ε1) при
Рисунок 3.2. Зависимость Т2/Т1
= f (ε2/ε1) при 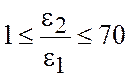 .
.
Следовательно, энергетическую светимость можно изменять как путем изменения температуры, так и подбором материала и характеристик излучающей поверхности. Подбирая материал и технологию обработки поверхности можно реализовать измерения энергетической светимости тела в широком диапазоне для нескольких стабильных температур.
В данной работе в
качестве источника теплового излучения используется поворотная сферическая
поверхность с разными коэффициентами излучения, что достигается с помощью
различной степени обработки поверхности. Материал одной полусферы – нержавеющая
полированная сталь, имеющая коэффициент теплового излучения ![]() =0,13, а материал другой полусферы –
нержавеющая сталь после пескоструйки, коэффициент теплового излучения которой
=0,13, а материал другой полусферы –
нержавеющая сталь после пескоструйки, коэффициент теплового излучения которой ![]() =0,7[5].
=0,7[5].
Определим энергетическую
светимость серого тела с коэффициентом теплового излучения ![]() =0,7 и
=0,7 и ![]() =0,13
и температурой Т=300К в спектральном диапазоне 5,5…7,5 мкм.
=0,13
и температурой Т=300К в спектральном диапазоне 5,5…7,5 мкм.
Положение максимума спектральной плотности потока излучения абсолютно черного тела определяется законом Вина:
![]() ,
(6)
,
(6)
где постоянная с принята равной 2898 мкмК
![]() мкм
мкм
Рассчитаем безразмерные величины хλ=λ / λ
х1= 5,5 / 9,66 =0,57;
х2=7,5 / 9,66 =0,78
По табличным данным найдем относительные значения спектральной плотности энергетической светимости z(xλ):
z(0,57)≈ 2,439 10-2;
z(0,78)≈ 0,1128
Определим энергетическую светимость абсолютно черного тела, соответствующую температуре 300К по закону Стефана-Больцмана:
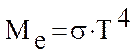 ,
(7)
,
(7)
где: ![]() =(5,6697
=(5,6697 ![]() 0,0029)
10-8 Вт/м2К4- постоянная Стефана-Больцмана;
0,0029)
10-8 Вт/м2К4- постоянная Стефана-Больцмана;
Т – температура тела.
Тогда
![]() Вт
Вт
Энергетическую светимость абсолютно черного тела в заданном спектральном интервале λ1…λ2 рассчитывают с помощью табличных функций z(xλ) = Ме(0…λ) / Ме(0…∞) в зависимости от безразмерных значений величины
хλ=λ / λ. Тогда
Ме(λ1 … λ2)= ![]() Т4 [ z(xλ2) - z(xλ2)]
Т4 [ z(xλ2) - z(xλ2)]
Для серого тела
Ме(λ1…λ2)= ![]()
![]() Т4
[ z (xλ2) – z (xλ2) ] (8)
Т4
[ z (xλ2) – z (xλ2) ] (8)
Тогда
Ме(5,5…7,5)= 28,42 Вт/м2
при ![]() =0,7
=0,7
Ме(5,5…7,5)= 5,28 Вт/м2
при ![]() =0,13
=0,13
Т.о. при температуре 300 К и коэффициенте излучающей поверхности 0,7 энергетическая светимость Ме = 28,42 Вт/м2 .
Рассчитаем эквивалентную температуру Тэ1, которой бы соответствовала энергетическая светимость равная Ме = 5,28 Вт/м2 при неизменном кэффициенте излучающей поверхности 0,7.
![]() ,
,
где: ![]() - безразмерный коэффициент теплового
излучения равный 0,7;
- безразмерный коэффициент теплового
излучения равный 0,7;
![]() =(5,6697
=(5,6697
![]() 0,0029) 10-8 Вт/м2К4-
постоянная Стефана-Больцмана.
0,0029) 10-8 Вт/м2К4-
постоянная Стефана-Больцмана.
Тогда
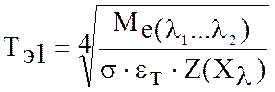 (9)
(9)
![]() К
или -75,30 0С.
К
или -75,30 0С.
Таким образом, изменением коэффициента теплового излучения мы получили две калибровочные точки (Т = 300 К, Т = 197,7 К) при постоянной температуре излучающей поверхности.
При температуре 300 К и коэффициенте излучающей поверхности 0,13 энергетическая светимость Ме = 5,28 Вт/м2 .
Рассчитаем эквивалентную температуру Тэ2, которой бы соответствовала энергетическая светимость равная Ме = 28,42 Вт/м2 при неизменном кэффициенте излучающей поверхности 0,13.
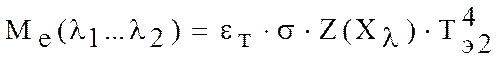
где: ![]() - безразмерный коэффициент теплового
излучения равный 0,13;
- безразмерный коэффициент теплового
излучения равный 0,13;
![]() =(5,6697
=(5,6697
![]() 0,0029) 10-8 Вт/м2К4-
постоянная Стефана-Больцмана.
0,0029) 10-8 Вт/м2К4-
постоянная Стефана-Больцмана.
Тогда
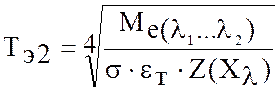 (10)
(10)
![]() К
или 185,96 0С.
К
или 185,96 0С.
Следовательно, мы получили еще две калибровочные точки (Т = 300 К, Т = 458,96 К) при постоянной температуре излучающей поверхности.
Таким образом, предложенный цилиндрический излучатель с поворотной сферической излучающей поверхностью позволяет реализовать измерения энергетической светимости тела в широком диапазоне при одной стабильной температуре.
4 ОБОСНОВАНИЕ И ВЫБОР СПОСОБА ТЕХНИЧЕСКОЙ
РЕАЛИЗАЦИИ ИСТОЧНИКА ИЗЛУЧЕНИЯ
Анализ известных принципов построения эталонных излучателей ИК диапазона (ИИК) позволяет рекомендовать для применения излучатели типа АЧТ с прямым (нагрев или охлаждение) воспроизведением требуемой температуры с помощью системы терморегулирования.
Если излучающая поверхность А тела имеет одинаковую температуру Т и одинаковый интегральный коэффициент излучения, то излучаемый телом поток определяется по формуле [3]
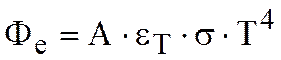 (10)
(10)
Из формулы следует, что для поддержания постоянства потока следует с высокой точностью поддерживать температуру тела, т.к. ее изменение наиболее резко сказывается на изменении потока, остальные множители в формуле являются константами для каждого конкретного тела.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.