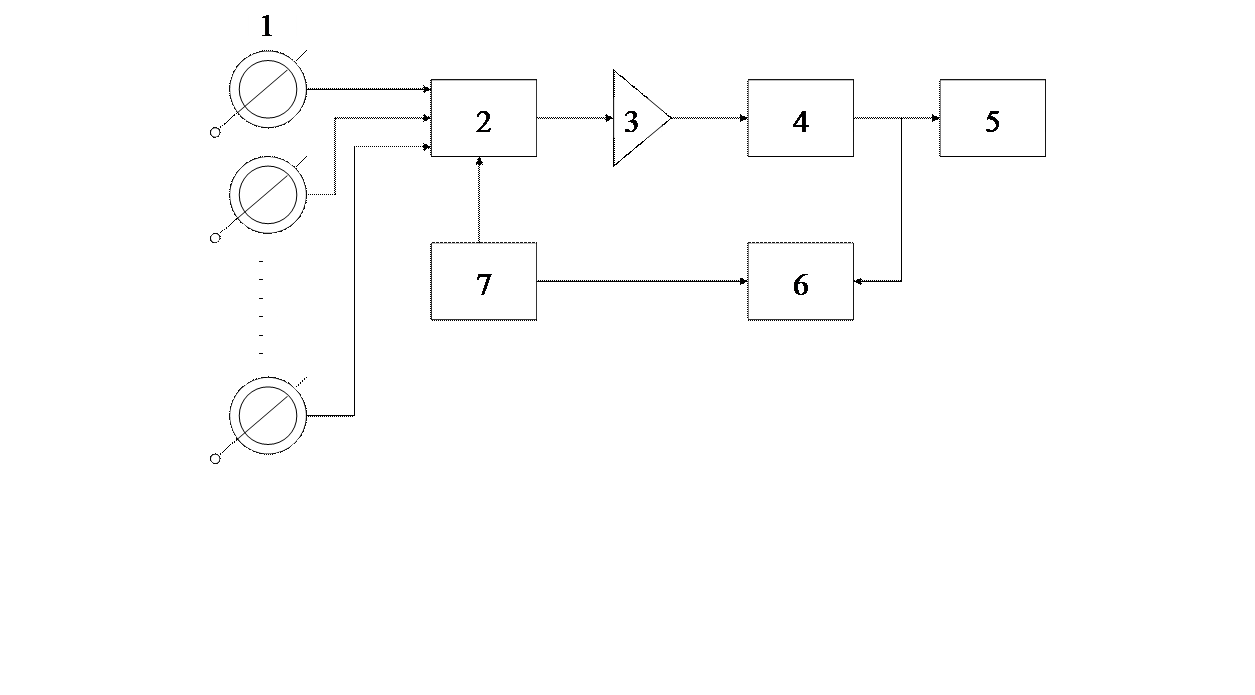
Разработка многоканального бесконтактного измерителя постоянных токов, страница 2

2. РАСЧЕТ ВЫВОДОВ НАВЕСНОГО ЭЛЕМЕНТА

Реальный навесной элемент (рис.1.а.) в зависимости от способа крепления заменяется математической моделью.  При колебаниях данного элемента на него будет действовать инерционная сила направленная перпендикулярно оси элемента и плоскости печатной платы (рис.2)

Расчет на вибропрочность

Вычислим длину вывода  l  от точки изгиба до радиоэлемента

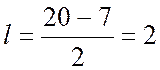  мм.                                        (2.1)

коэффициентт k  будет равен

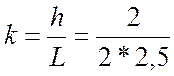 = 0,375 мм.                                (2.2)

 Момент инерции поперечного сечения равен

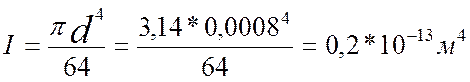                        (2.3)

где d  -  диаметр вывода элемента.

Тогда собственная частота для принятой модели составит

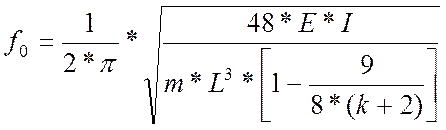     ,                  (2.4)

где  Е - модуль упругости первого и второго рода материала выводов навесных элементов,;

m-масса навесного элемента, кг;

, l-длина вывода от точки загиба до тела элемента, м;

к - коэффициент  равный ;

I-осевой момент инерции на выводах навесного элемента,;

;

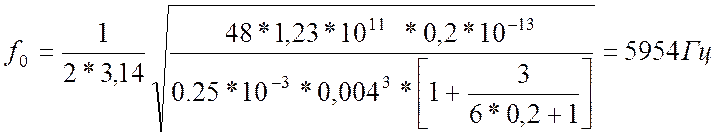Определим коэффициент настройки или частотное отношение по формуле (2.5):

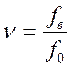   ,                                            (2.5)

где -max частота вибраций действующих на рассматриваемый объект

Коэффициент расстройки меньше 0,5, следовательно, величину инерционной силы, действующей на элемент, находим из уравнения (2.6):

 ,                                 (2.6)

где m-масса навесного элемента;

g-ускорение свободного падения, равное 9,8 м/с;

Определим изгибающий момент, действующий в характерных точках  рамы по формуле (2.7):

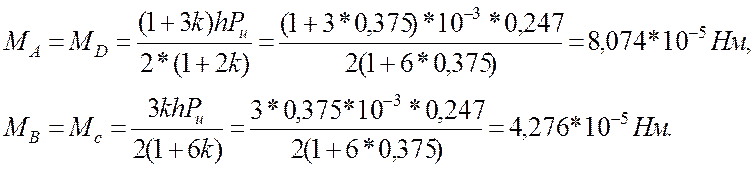
Определим изгибные напряжения в точке действия наибольшего изгибного момента по формуле 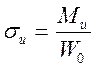(2.8):

 ,                                          (2.8)

где -max изгибающий момент;

-осевой момент сопротивления сечения провода.

 ;

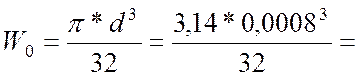
Па

Определим побочные напряжения в рассматриваемой точке.

напряжение сдвига найдем из уравнения (2.10) , предварительно определив площадь поперечного сечения вывода по формуле (2.9):

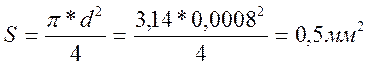                         (2.9).

                   (2.10)

Определим эквивалентные напряжения по формуле (2.11):

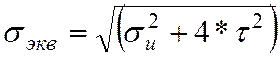                           (2.11)

а

Допускаемое напряжение будет равно:

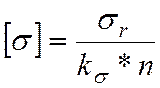  ,                                (2.12)

где-предел усталости,    

=1,2;

n - коэффициент запаса =2.

 .

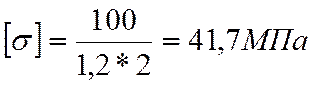Проверяем условие прочности выражением:

                                  (2.13)

2,8<41,7.

Условие выполняется, поэтому переходим к расчету на статическую прочность.

Инерционную силу, приложенную к модели при одновременном действии линейных, ударных и вибронагрузок определим, используя выражение:

  ,                  (2.14)

где  - линейные нагрузки;

 - ударные нагрузки.

Используя полученное  определяем изгибающий момент по формуле(2.7):

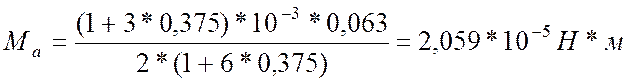
изгибное напряжение по формуле (2.8):

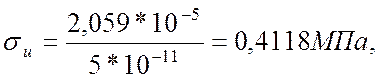
и напряжение сдвига по формуле(2.9):

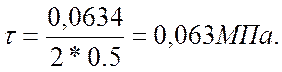
Эквивалентное напряжение будет равно:

По формуле(2.15)  определим допускаемое напряжение:

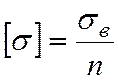   ,                                  (2.15)

где  -предел прочности материала вывода.

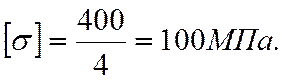
Проверяем выполнение неравенства (2.13) из условия статистической прочности:

49,15<100

Неравенство выполняется как из условия динамической, так и статической прочности, следовательно, примененный способ крепления обеспечивает работоспособность радиоэлемента в заданных условиях эксплуатации.

3. РАСЧЕТ ПЕЧАТНОЙ ПЛАТЫ

Печатный узел обладает собственной резонансной частотой колебаний f₀, зависящей от таких параметров, как габариты, масса, способ крепления и т.д. В соответствии с существующими нормами печатные узлы без амортизации должны иметь f₀ больше 60 Гц. Как и для навесных элементов, для печатных узлов должно выполняться требование отсутствия резонанса, когда частота вынужденных колебаний f_в близка к собственным. Вибрационные нагрузки, прежде всего, сказываются на величине прогиба печатной платы, зависящего от её жёсткости и влияющего на её прочность.

Необходимо выполнить расчет на прочность и жесткость печатной платы из фольгированного стеклотекстолита площадью 150´100 мм толщиной 1.5 мм. На плате установлены: резисторы, диоды, конденсаторы, микросхемы, кварц, разъемы, резисторные сборки, транзисторы. Для диода ??? выполнить расчет на прочность выводов при условии, что он установлен на плате горизонтально без дополнительного крепления, а нагрузка приложена вдоль его оси. Расстояние между центрами монтажных отверстий 20 мм, между осью элемента и платой 5 мм. Печатный узел предназначен для установки в лабораториях, может перевозиться автомобильным транспортом.

Для указанного случая применения из табл. 1.3 [1] находим соответствующие условия эксплуатации.

Выбираем расчетную модель, уподобляя печатную плату пластине с равномерно распределенной нагрузкой и определяем собственную частоту колебаний по формуле:

f₀ = 0.159 · К_a (Е · Н_п³ / 12 · m'')^0.5 / а² ,              (3.1)

где k_a - коэффициент, завивсящий от способа крепления пластины, находится по формуле:

К_a = 9.87·(1+2.57а²/b²+5.14а⁴b⁴)^0.5,                   (3.2)

К_a=56.25

а – длина платы (большая сторона), a=0.15 м;

b – ширина платы (меньшая сторона), b=0.10 м;

Е– модуль упругости материала основания платы, Н/м²;

Н_п – толщина печатной платы, м;

m"- распределённая по площади масса, кг/м², которая находится по формуле:

m"=(m_э + m_п) / аb,                                     (3.3)

где m_э – суммарная масса навесных элементов, кг;

m_п – масса печатной платы, кг.

m_п = r×а×b×H_п                                                                         (3.4)

r  - плотность материала основания, кг/м³.

m_п = 1.6×10³ × 0.15 ^. 0.10 ^. 1.5^.10^-3 = 0.036 кг.

m" = (0.035 + 0.036)/0.15 ^. 0.10 = 4.73  кг/м².

f₀ = 0.159 ^. 56.25 ^. (3 ^. 10^{10 .} (1.5 ^. 10^-3)³ / 12 ^. 4.73^)0.5 / 0.15² =

= 507 Гц

По полученному значению f₀ из выражения (3.5) определяем коэффициент расстройки n:

n = f_в /f₀                                            (3.5)

n = 15/507=0.029

Проверяем условие (3.6):

                                    (3.6)

Условие не выполняется, следовательно, печатный узел не работает в резонансной зоне. Переходим к расчету на прочность и жесткость.

Определяем амплитуду смещения платы на собственной частоте по формуле(3.7):

А₀ = 250 · n_в / f₀²                                   (3.7)