Разработка вторичного эталона единицы длины для измерения уровня жидкости, страница 11

Эта погрешность определяется свойствами жидкости, прежде всего, коэффициентом поверхностного натяжения, вызывающего явление мениска, и электропроводностью жидкости; а также свойствами электронной аппаратуры эталона (стабильностью работы и чувствительностью компаратора). Из-за сложного характера зависимостей характеристик прибора и свойств жидкости эту погрешность целесообразно оценить экспериментальным путем. Результаты экспериментального определения погрешности приведены в разделе /2.3/.

2.4.3.3  Погрешность установки начального положения ОДУ-э.

Эта погрешность  определяется точностью “пристыковки” электроконтактного щупа к плоскости отсчетного фланца, а также, точностью обработки поверхности установочного фланца и пристыковочной части ОДУ-э. Погрешность установки начального положения ОДУ-э примем ±0,1мм. Эта погрешность носит случайный характер. Приняв равномерный закон распределения случайной составляющей погрешности, определим среднеквадратическое отклонение случайной составляющей погрешности по формуле:

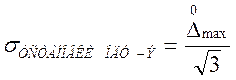,                                    (2.15)

где      – максимальное отклонение ОДУ-э от начального (установленного) положения, .

Тогда случайная составляющая погрешности

                    .

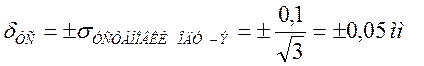2.4.3.4  Погрешность рулетки.

Согласно ГОСТ 7502-89 “Рулетки измерительные металлические” погрешность рулетки составляет ±0,3мм на длине измерения 1м. Так как, используемая в экспериментах настоящей работы длина рулетки составляет 1м, то границами данной погрешности можно считать ±0,3мм. Приняв равномерный закон распределения случайной составляющей погрешности, определим среднеквадратическое отклонение случайной составляющей погрешности по формуле:

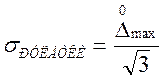                                         ,                                              (2.16)

где      – максимальная погрешность рулетки, .

Тогда случайная составляющая погрешности равна

.

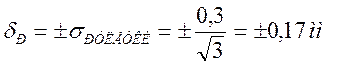2.4.3.5  Погрешность определения длинны тела ОДУ-э от верхнего упорного конца до конца иглы.

Эта погрешность  определяется ошибкой при определении длинны тела ОДУ-э от верхнего упорного конца до конца иглы. Погрешность при определении этой длинны, с помощью штангенциркуля составляет ±0,1мм. Данная погрешность носит случайный и систематический характер. Приняв равномерный закон распределения случайной составляющей погрешности можно определить среднеквадратическое отклонение случайной составляющей погрешности по формуле:

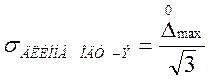                              ,                                                  (2.17)

где      – максимальная погрешность при определении длинны тела ОДУ-э, .

Тогда случайная составляющая погрешности равна:

.

2.4.4  Оценка дополнительных погрешностей.

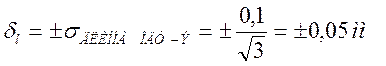2.4.4.1  Упругое удлинение мерной ленты под воздействием веса ОДУ-э.

Вес ОДУ-э вызывает упругое растяжение мерной ленты и приводит к изменению длины измерительного участка рулеточной ленты, вследствие упругой деформации.

Деформация растяжения рулеточной ленты характеризуется абсолютным удлинением , равным разности длин образца до растяжения  и после него :

                                                   .                                             (2.18)

Отношение абсолютного удлинения  к длине рулеточной ленты  называется относительным удлинением:

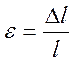                                                   .                                                 (2.19)

При деформации тела возникают силы упругости. Физическая величина, равная отношению модуля силы упругости к площади сечения тела называется механическим напряжением :

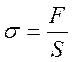                                                   ,                                                 (2.20)

где      – сила тяжести ОДУ-э равная , ;

           – площадь сечения рулеточной ленты, .

Тогда механическое напряжение равно:

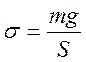                                                   ,                                               (2.21)

где      – масса стержня щупа, ;

           – ускорение свободного падения, примерно равно .

При малых деформациях напряжение прямо пропорционально относительному удлинению:

                                                   ,                                              (2.22)

где      – коэффициент пропорциональности, который называется модулем упругости.

Модуль упругости рассчитывается из следующего выражения:

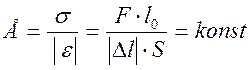                                         .                                  (2.23)

Металлическая рулеточная лента выполнена из углеродистой стали. Модуль упругости углеродистой стали .

Линейные размеры рулеточной ленты следующие: длина , диаметр , толщина .

Тогда площадь сечения мерной рулеточной ленты равна:

                                         .                    (2.24)

Рассчитаем массу стержня щупа из выражения для плотности вещества:

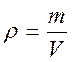                                                   ,                                                 (2.25)

где      – масса стержня, ;

           – объем тела, .

Из формулы (2.25) определим массу стержня:

                                                   .                                              (2.26)

Стержень щупа изготовлен из латуни, для латуни .

Стержень имеет следующие линейные размеры: диаметр , а его длина , следовательно, объем стержня найдем по формуле:

                                                   .                                          (2.27)

Подставляя (2.27) в (2.26) получим:

                                                   .                                     (2.28)

Рассчитаем массу стержня:

.

Из формулы (2.23) получим выражение для определения абсолютного удлинения мерной рулеточной ленты , при ее длине :

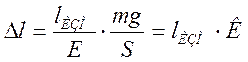                                         ,                                  (2.29)

где     .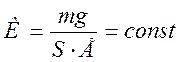

Из данной формулы можно получить абсолютное удлинение мерной ленты; например при .

.

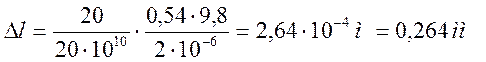Таким образом, эта погрешность является функцией длины ленты  и носит в основном систематический характер, и при необходимости может быть учтена в результатах измерений.