







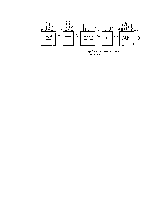

4. ПОСТРОЕНИЕ МЕТРОЛОГИЧЕСКОЙ МОДЕЛИ
Метрологическая модель используется для определения метрологических характеристик средства измерения, расчета погрешностей средства измерения и результатов измерений.
Для получения метрологической модели всего канала составляется модель измерительных блоков, после объединения которых, получаем полную модель.
4.1 Упругий элемент первичного измерительного преобразователя. На упругий элемент воздействуют следующие факторы: влажность, пыль, температура окружающей среды, старение, ползучесть.
4.1.1
Влажность и пыль как влияющий фактор можно не учитывать,
благодаря герметизации упругого элемента.
4.1.2
Изменение температуры окружающей среды
приводит к
изменению модуля Юнга Е материала упругого элемента и, следовательно, к
изменению относительной деформации e1. Упругий
элемент изготовлен из
стали 40x13, которая имеет температурный коэффициент модуля упругости
ТКЕ=2*1051/°С.
Т. к. температурный коэффициент модуля упругости имеет следующую
|
|
|
то аддитивная погрешность от изменения температуры на 10 0С составит: |
зависимость от модуля упругости:
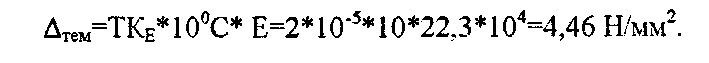
|
|
Приведенная погрешность:
Эта погрешность имеет равномерный закон распределения. Поэтому
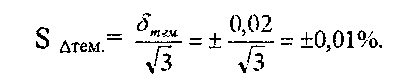
Погрешность от изменения температуры является мультипликативной погрешностью.
4.1.3 Возникающие
процессы старения обуславливают изменение
модуля упругости. Они зависят не только от свойств материала, но и от
его
обработки. Поэтому для
изготовления упругого элемента датчика
существенное значение имеет термическая обработка. Благодаря выдержке
материала устраняется влияние процессов
старения.
4.1.4 Ползучесть упругого элемента в значительной
степени зависит от
свойств материала. Материалы для
упругих элементов должны обладать
высокой релаксационной стойкостью, стабильностью упругих свойств во
времени и в переменных внешних
условиях. Все технические расчеты на
упругую деформацию материалов
основываются на законе Гука, но при определении точных значений деформаций при
приложении нагрузок обнаруживаются отклонения от этого закона,
которые объясняются несовершенствами упругих материалов. Явление
несовершенной упругости обнаруживается при нагружении и разгружении
нагрузками, не превышающими предел упругости. К указанным
явлениям относится релаксация напряжения, которая заключается в
постепенном падении напряжений в нагруженном упругом теле.
Релаксация напряжений является временной характеристикой.
4.2 Тензорезисторы. На тензорезисторы воздействуют следующие факторы: влажность, пыль, температура окружающей среды, ползучесть.
4.2.1 Влажность и
пыль как влияющий фактор можно не учитывать, т.
к. тензорезисторы после приклеивания
к упругому элементу покрывают
лаком (герметизируют).
4.2.2 Температура
приводит к изменению сопротивлений
тензорезисторов. В крановых
весах предусмотрена температурная
компенсация, которая позволяет
корректировать результат измерения с
учетом температурного изменения
сопротивлений.
4.2.3 При
скачкообразных нагрузках появляется ползучесть. Под
ползучестью понимают
произвольное изменение сопротивления при
постоянном уровне напряжения. Значение
ползучести составляет порядка
2*10-4. Эта
погрешность имеет равномерный закон распределения,
следовательно Sпол=0,0001
4.3 Измерительная схема.
На измерительную схему воздействуют следующие факторы: изменение напряжения питания, температура окружающей среды, начальный разброс сопротивлений тензорезисторов, контактные ЭДС.
4.3.1 Для того чтобы уменьшить влияние изменения напряжения питания на результат измерения необходимо использовать высокостабильный источник питания. Источник питания, используемый в данной схеме, приводит к погрешности a =0,002%. Эта погрешность имеет равномерный закон распределения. Поэтому
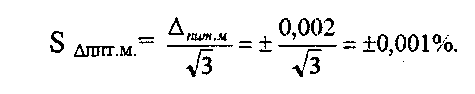
4.3.2 Температура окружающей среды влияет на:
-сопротивление тензорезисторов;
- сопротивление проводов;
Влияние температуры на сопротивление тензорезисторов несущественно, поскольку используется компенсационный терморезистор. Т. е. в этом случае влияние температуры не учитывается.
Изменение температуры влияет на контактные и переходные сопротивления медных проводов. Сопротивление зависит также от длинны провода (1). Для медных проводов: 1=30м, Sсеч= 0.35 мм2, р=0,0178 0m/mm2/m, ТКО - 0,4% / °С.
|
|
|
Изменение сопротивления линии при изменение температуры на 10 °С: |
|
|
|
Погрешность контактных сопротивлений медних проводов: |
|
|
|
Эта погрешность имеет равномерный закон распределения. Поэтому: |
|
|
Сопротивление линии с медного провода:
4.3.3 Влияющим фактором является начальный разброс сопротивений тензорезисторов. После того как тензорезисторы были приклеены к упругому элементу, у них действительно существует разброс сопротивлений. Но этот влияющий на погрешность фактор можно исключить, используя подстроечный резистор, который присутствует в измерительной схеме.
4.3.3 Одним из наиболее влияющих факторов является контактные ЭДС. Они достигают десятки милливольт. Эти ЭДС постоянны. Работа схемы осуществляется на переменном токе, т. е. путем синхронного детектирования подавляются контактные ЭДС.
4.4 Нормирующий преобразователь
Нормирующий преобразователь построен на операционных усилителях, на которые влияют следующие факторы: изменение температуры окружающей среды, колебания напряжения питания.
4.4.1 Изменение температуры окружающей среды вызывает смещение нуля усилителя DСМ.Н.Q= 2мкВ/10°С по входу, которое является
|
|
|
Выразим ее в относительных единицах, т. е. пронормируем: |
|
|
|
Закон распределения примем равномерным, тогда |
|
|
аддитивной составляющей погрешности. Приведенная к выходу, эта погрешность будет составлять:
4.4.2 Колебания напряжения питания вызывают
|
|
|
В относительных единицах: |
|
|
|
Закон распределения примем треугольным, тогда |
|
|
смещение нуля усилителя на величину 0,1 мкВ / 10% Uпит.
Эта погрешность является несущественной, ею можно пренебречь. изменение коэффициента на величину 0,01%/10% Ипит. Максимальное изменение коэффициента усиления от влияния колебаний напряжения питания:
|
|
В относительных единицах:
|
|
Примем закон распределения треугольным, тогда
|
|
Эта оценка является мультипликативной составляющей погрешности.
4.5. Аналого-цифровой преобразователь
Основними факторами, которые влияют на АЦП, являются погрешность квантования, нелинейность характеристики, температура и нестабильность напряжения птиания.
4.5.1 Погрешность квантования для выбранного АЦП составляет 1кг. Относительное значение квантования, приведенное к пределу, составляет:
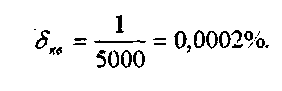
Для погрешности квантования характерно равномерное распределение:
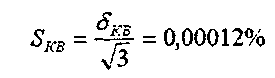
Данная погрешность является аддитивной, т. к. она постоянна по всему диапазону.
4.5.2 Погрешность АЦП, вызванная нелинейностью характеристики, является мультипликативной погрешностью. Ее граничной оценкой является ± 3 единицы младшего разряда Dнел = ±3ед = ±3кг. Для определения оценки среднеквадратической погрешности необходимо знать закон ее распределения. Для большинства цифровых средств измерений в связи с обязательным присутствием операций дискретизации и квантования закон распределения близкий к равномерному и значение среднеквадратической погрешности будет составлять:
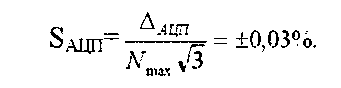
4.5.3 Влияние температуры вызывает смещение "нуля" на одну единицу наименьшого разряда на каждые 10 °С:
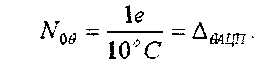
Температурная погрешность не зависит от измеряемой величины, т. е. она является адитивной погрешностью. Максимальная температурная погрешность составляет:
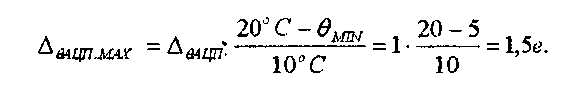
Температурная среднеквадратическая погрешность определяется при известном законе распределения. Для температурных влияний закон распределения близкий к нормальному. Задаёмся доверительной вероятностью Рдов=0,95 и по таблице функции Лапласса находим 1=1,76.
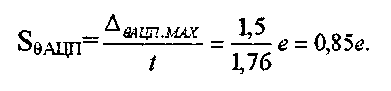
В
относительных единицах ![]() = 0,085%.
= 0,085%.
4.5.2
Влияние нестабильности напряжения питания составляет 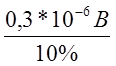
(смещение "нуля").
Эта погрешность распределена по равномерному закону и является адитивной. Оценка среднеквадратической погрешности составляет:
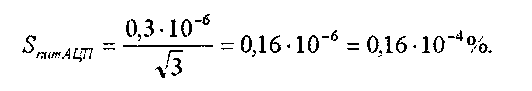
Эта погрешность на несколько порядков ниже, чем температурная, а следовательно ее можно не учитывать.
Индикатор и микропроцессор в метрологическую модель не входят, поскольку их функции заключаются не в преобразование информации, а соответственно в индикации информации и в управление ею.
После составления моделей измерительных блоков и их объединения получаем полную модель (Рисунок 4.1):
|
|
Рисунок 4.1 Метрологическая модель цифровых крановых весов.
Погрешность этого измерительного канала определяем как:
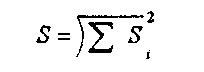
Общая аддитивная погрешность: S = ±0,09%. Общая мультипликативная погрешность: S = ±0,07%.
Общая погрешность: S = (Sадд+Sсм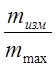 )%
= (0,09+0,07
)%
= (0,09+0,07 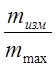 )%.
)%.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.