










МОДЕЛИРОВАНИЕ НА ЭВМ
ВИДЫ МОДЕЛИРОВАНИЯ
При выполнении моделирования определяется тип системы подлежащей моделированию. Все объекты исследования при этом рассматриваются с точки зрения системного подхода. Системный подход предполагает выделение в объекте значимых параметров В вектора возмущающих воздействий U, вектора шумов V, а также векторов состояния X, наблюдения Y, внутреннего состояния Z, которые находятся в области задач.
В технической кибернетики для упрощения вычислений принимается пространство задач BZ,лежащее в евклидовом пространстве или банаковом пространстве. Евклидово пространство характеризуется прямоугольной системой координат, для которой неравенство Коши-Кониковского переходит в равенство. В этом случае система может определяться, как Декартово произведение векторов. Система может быть описана в виде функции:
![]()
или, в общем случае, в виде функционала:
X=A[x, V].
Система предполагает:
- возможность декомпозиции;
- возможность интеграции;
- возможность модульного представления;
- функциональность отдельных элементов;
- и наличие целевой функции.
В зависимости от выбранной классификации системы могут подразделяться по:
1. размерностям:
- одномерные;
- двумерные;
- многомерные.
2. протеканию процессов:
- статические системы;
- динамические.
3. изменению значения параметров:
- стационарные;
- нестационарные (стохастические).
4. природе реализации:
- электрические;
- физические;
- химические;
- биологические;
- социальные и др.
Целью моделирования можно назвать процесс замещения системы одного типа с системой другого типа функционирования, природы или описания для обеспечения лучшей наглядности и выяснения механизма функционирования.
Моделирование на ЭВМ – это реализация какой-либо системы какой-либо системы в виде системы функционирования ЭВМ:
а) дискретная реализация мат. модели для ЭВМ;
б) реализация в виде электрических процессов для аналоговой вычислительной машины (АВМ).
МАТИМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ
Большинство технических систем описывается динамическими моделями 1, 2 и более высоких порядков. Общий вид динамической системы обычно записывается путем учета производной по вектору состояний в зависимости от других параметров.
![]()
За такой системой выполняется наблюдение с помощью уравнения наблюдения:
Y(t)=d(x, V)
V – вектор шумов.
Для систем, которые описываются динамическими уравнениями высоких порядков, используется матричное представление:
![]()
![]()
![]()
![]()
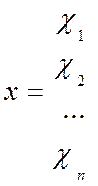 ,
, 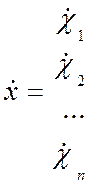 .
.
В случае, если система линейна по параметрам, то последнее уравнение можно записать в виде произведений матриц:
![]()
А – матрица коэффициентов.
Эта же система может быть записана в виде n уравнений 1-го порядка (стандартная форма Коши):
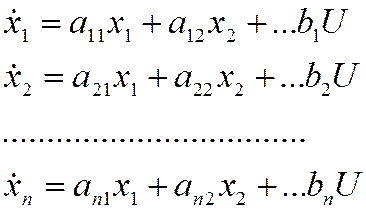
На ЭВМ интегрирование диф. уравнений может быть выполнено с помощью формулы дискретного интегрирования Коши.
Интегрирование по методу
Коши заключается в следующем: для уравнения ![]() производная
производная
![]() находится как разность значений
находится как разность значений ![]() , отнесенная к
разнице аргумента х2 – х1 , что при минимизации последней
соответствует определение производной:
, отнесенная к
разнице аргумента х2 – х1 , что при минимизации последней
соответствует определение производной:
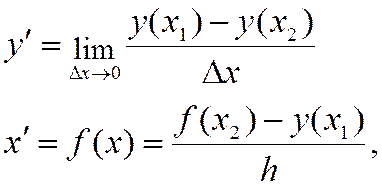
![]()
h – шаг интегрирования.
Если переменные состояния х1 , х2 и т.д. будут соответствовать различным временным интервалам, то можно с изменением параметров А и В получить:
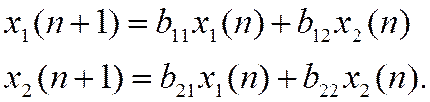
Таким образом, система диф. уравнений может быть описана в виде системы конечноразностных уравнений, которые легко реализуются на ЦВМ.
Моделирование динамических систем на АВМ не требует обязательного перевода в дискретную форму, т.к. содержат динамические элементы в своем наборе.
Пример:
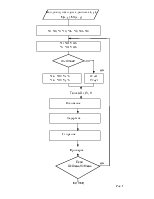
Необходимо произвести декомпозицию на элементы АВМ динамической системы 2-го порядка.

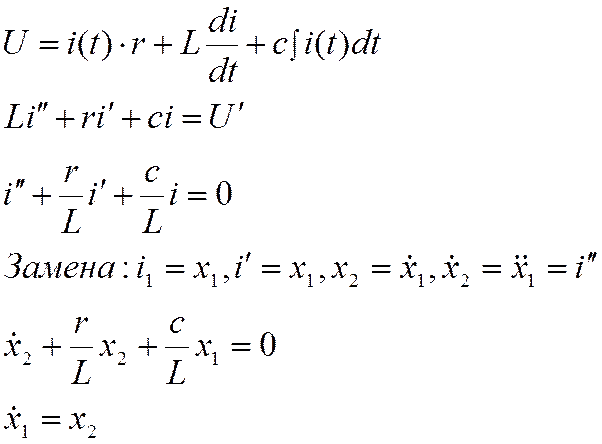
Запишем в форме Коши:
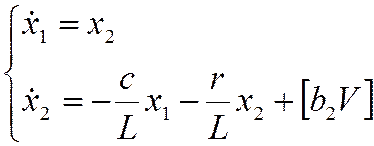 (1.1)
(1.1)
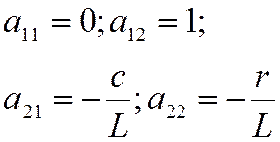
МОДЕЛИРОВАНИЕ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ С УЧЕТОМ ЗОНЫ НЕЧУВСТВИТЕЛЬНОСТИ
Все измерительные приборы имеют определенный порог чувствительности. Рассмотрим в качестве измерительного устройства датчик линейных ускорений.
Система 1.1 полностью описывает динамику процесса за исключением уравнения наблюдения.
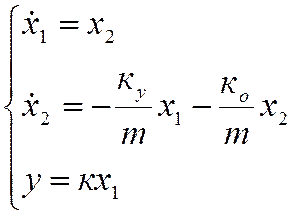 (3.2)
(3.2)
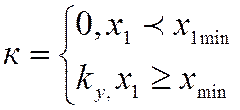
Переключение различных коэффициентов усиления осуществляется в электронном виде мультиплексором, который коммутирует сигналы в одном или разных направлениях при заданном адресе коммутации. Мультиплексоры бывают дискретные и аналоговые (ключи).
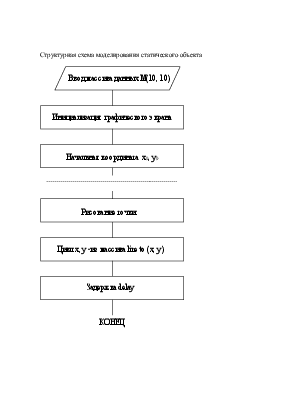
Зарисуем структурную схему моделирования
Основным рядом машин предназначенных для моделирования и управления были машины серии СМ (СМ-2, СМ-4 и др). Особенностью их являлась работа в многозадачном режиме и режиме реального времени, под управлением операционной системой ОС-РВ. Это важно для процессов, привязанных ко времени таких как интегрирование динамических величин.
Простейшим видом моделей является визуализация. Для набора статических данных х, у можно построить ломанную прямую.
|
х |
х1 |
х2 |
|
|
у |
у1 |
у2 |
|
![]()
![]()
Второй этап визуального моделирования – интерполяция кривой. Для этого используется:
1) интерполяционный полином Лагранжа;
2) интерполяционный полином Фурье.
Третий шаг – построение трехмерных графиков.
Четвертый этап – 3Д технологии (затенение объекта). Формирование полутоновых пикселей требует большого времени вычислений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.