изучение временных характеристик типовых динамических звеньев с использованием автоматизированных средств моделирования ПК – MATLAB, SIMULINK

Министерство образования и науки Украины

Национальный аэрокосмический университет им. Н.Е.Жуковского

«Харьковский авиационный институт»

Кафедра 301

Основы работы и простейшие вычисления в Matlab

ХАИ.ЛР.6.051002.338.09

Отчет

по лабораторной работе №1

по курсу «Теория автоматического управления»

Исполнитель: студентка 338 группы

Рыбалко С.П.

Проверил: к.т.н., проф.

Суббота А.М.

ассистент

Копысов О.Э.

2010

Цель работы: целью работы является изучение временных характеристик типовых динамических звеньев с использованием автоматизированных средств моделирования ПК – MATLAB, SIMULINK.

Таблица 1 – Типовые динамические звенья

	Название звена	Передаточная функция звена
1	Интегрирующее
2	Апериодическое 1-го поядка (инерционное)
3	Апериодическое 2-го порядка (колебательное звено)	Т1<2T2
4	Реальное диференцирующее
5	Форсирующее
6	Изодронное

Таблица 2 – Исходные данные

№ вар	Апер Иод звено		Апериодич.звено 20го порядка			Ин- тегр звено	Изодо. звено		Реальное Диф. звено		Инерц.-форс звено
	К	Т	К	Т		К	К1	К2	К		К	Т0	Т
1	2	0,2	1	0,2	2,0(0,2)	2	2	0,5	2	0,4	2	2	0,8

Часть 1

Таблица 3 – Экспериментально полученные характеристики при вариации параметров каждого звена

Рисунок 3.1- Схема интегрирующего звена с изменением К

plot(a(:,1),a(:,2),’—‘,a(:,1),a(:,3),’o’,a(:,1),a(:,4),’*’)

legend(‘K1=1.8’,’K2=2’,’K3=2.2’)

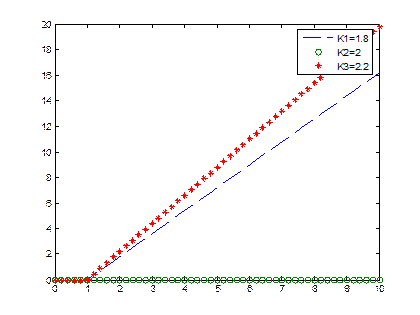
Рисунок 3.2- График интегрирующего звена с изменением К

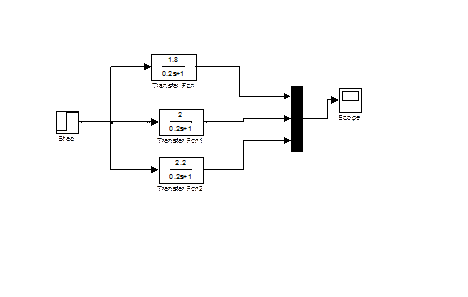
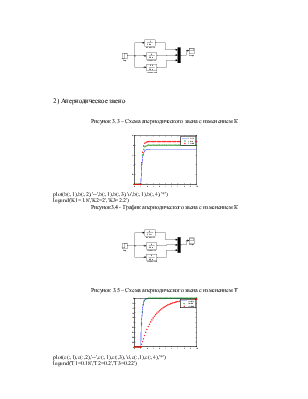
2) Апериодическое звено

Рисунок 3.3 – Схема апериодического звена с изменением К

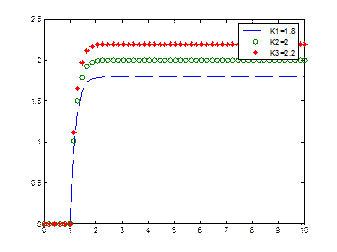
plot(b(:,1),b(:,2),'--',b(:,1),b(:,3),'o',b(:,1),b(:,4),'*')

legend('K1=1.8','K2=2','K3=2.2')

Рисунок3.4 - График апериодического звена с изменением К

Рисунок 3.5 – Схема апериодического звена с изменением Т

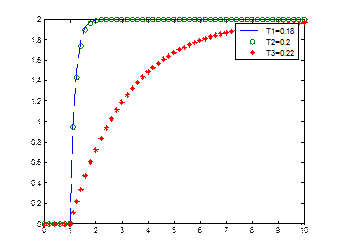
plot(c(:,1),c(:,2),'--',c(:,1),c(:,3),'o',c(:,1),c(:,4),'*')

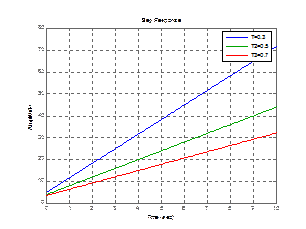
legend('T1=0.18','T2=0.2','T3=0.22')

Рисунок 3.6 – График апериодического звена с изменением Т

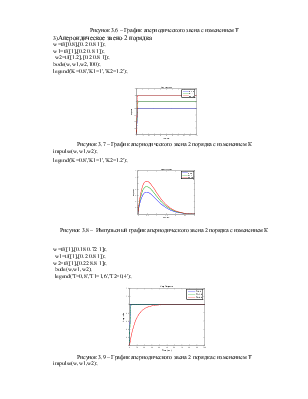
3)Апероидическое звено 2 порядка

w=tf([0.8],[0.2 0.8 1]);

w1=tf([1],[0.2 0.8 1]);

 w2=tf([1.2],[0.2 0.8 1]);

bode(w,w1,w2,100);

legend('K=0.8','K1=1','K2=1.2');

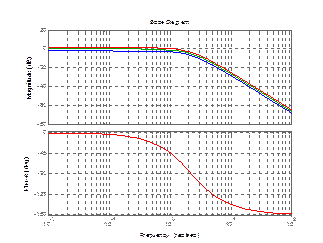
Рисунок 3.7 – График апериодического звена 2 порядка с изменением К

impulse(w,w1,w2);

legend('K=0.8','K1=1','K2=1.2');

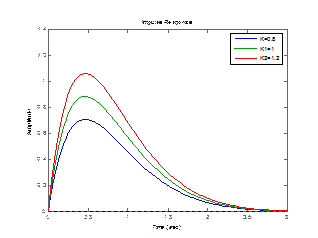
Рисунок 3.8 –  Импульсный график апериодического звена 2 порядка с изменением К

w=tf([1],[0.18 0.72 1]);

 w1=tf([1],[0.2 0.8 1]);

w2=tf([1],[0.22 8.8 1]);

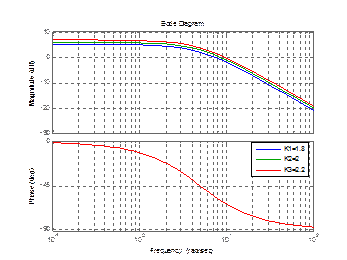
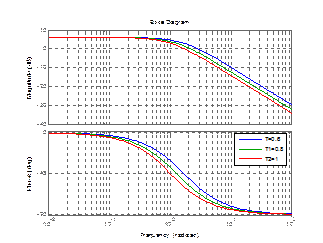
 bode(w,w1,w2);

 legend('T=0,8','T1=1,6','T2=0,4');

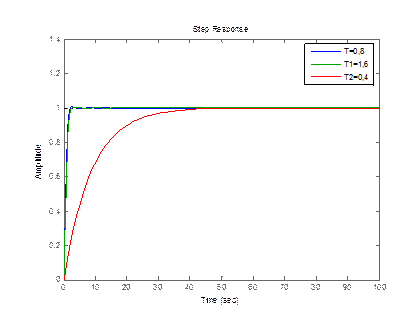
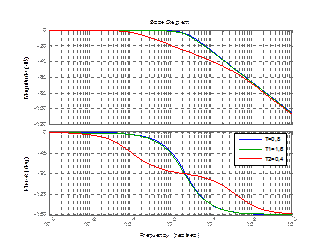
Рисунок 3.9 – График апериодического звена 2 порядка с изменением Т

impulse(w,w1,w2);

 legend('T=0,18','T1=0,2','T2=0,22');

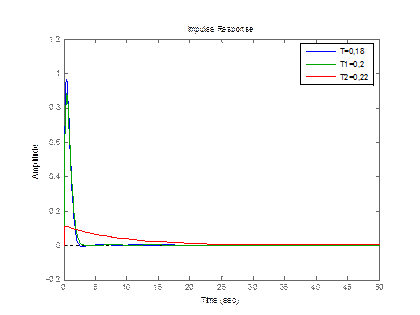
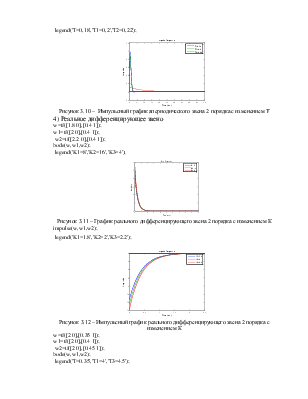
Рисунок 3.10 –  Импульсный график апериодического звена 2 порядка с изменением Т

4) Реальное дифференцирующее звено

w=tf([1.8 0],[0.4 1]);

w1=tf([2 0],[0.4 1]);

 w2=tf([2.2 0],[0.4 1]);

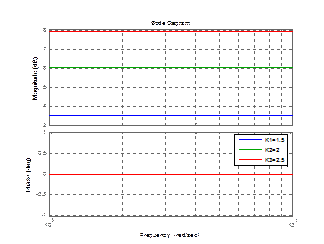
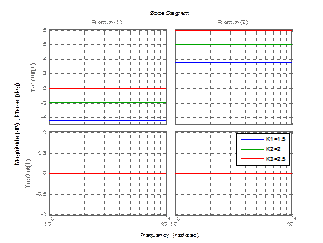
bode(w,w1,w2);

 legend('K1=8','K2=16','K3=4');

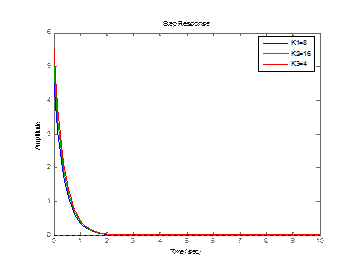
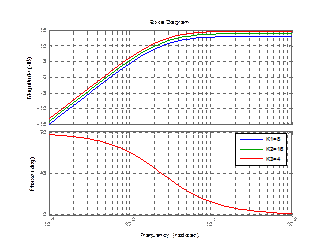
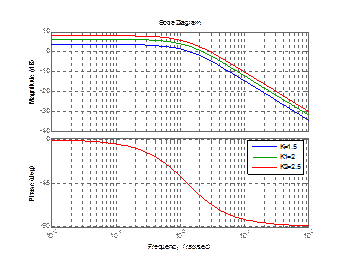
Рисунок 3.11 – График реального дифференцирующего звена 2 порядка с изменением К

impulse(w,w1,w2);

 legend('K1=1.8','K2=2','K3=2.2');

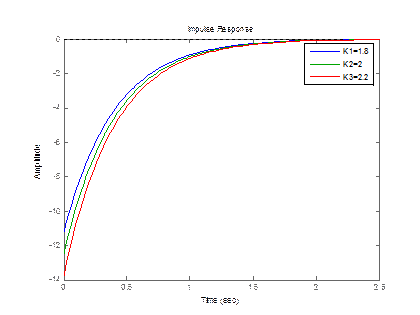
Рисунок 3.12 – Импульсный график реального дифференцирующего звена 2 порядка с изменением К

w=tf([2 0],[0.35 1]);

w1=tf([2 0],[0.4 1]);

 w2=tf([2 0],[0.45 1]);

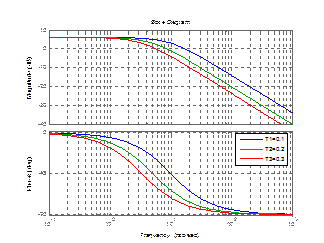
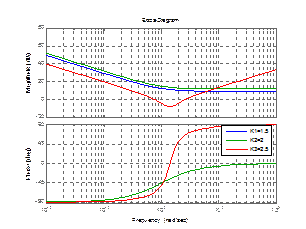
bode(w,w1,w2);

 legend('T=0.35','T1=4','T3=4.5');

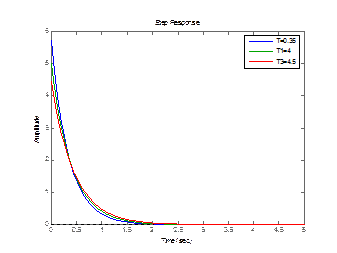
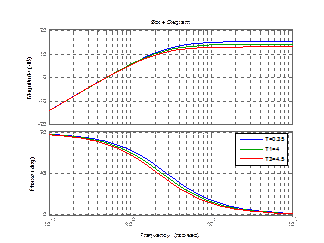
Рисунок 3.13 – График реального дифференцирующего звена 2 порядка с изменением Т

impulse(w,w1,w2);

legend('T=3.5','T1=4','T3=4.5');

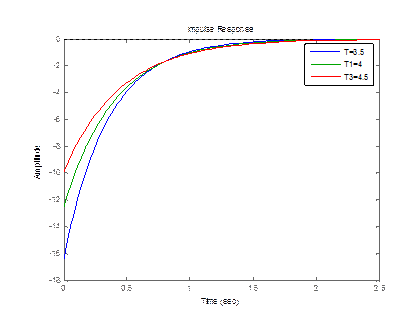
Рисунок 3.14 – Импульсный график реального дифференцирующего звена 2 порядка с изменением Т

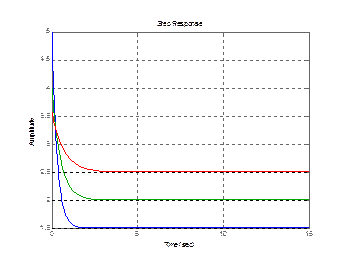
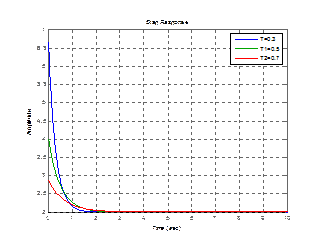
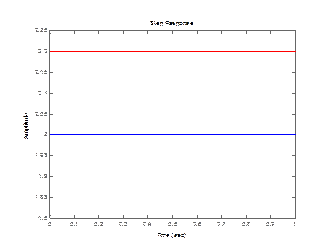
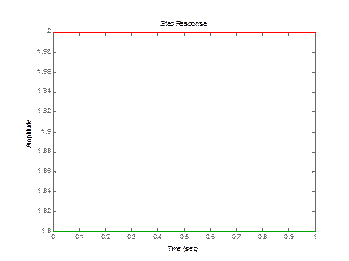
5) Инерционно-форсирующее (реальное форсирующее) звено