Проверка прочности наклонных сечений, страница 2

                  В формулах (3.50) и (3.51): Q – поперечная сила от внешних нагрузок в конце наклонного сечения. В практических расчетах часто в эти формулы подставляют величины поперечной силы у опорного вертикального сечения, что идет в запас прочности наклонного сечения.

                  Анализ формул (3.52)…(3.55) показывает, что величина поперечной силы, воспринимаемой наклонным сечение, от его проекции c зависит неоднозначно. С увеличением с увеличивается число пересекаемых наклонным сечением хомутов и отгибов, т.е. увеличиваются два первых числа в формуле (3.52), но в то же время уменьшается поперечная сила Q_b, воспринимаемая бетоном сжатой зоны. Следовательно, наиболее опасным будет сечение, в котором правая часть условия (3.52) будет минимальной.

Невыгоднейшее наклонное сечение следует определять путем сравнительных расчетов из условия минимума поперечной силы, воспринимаемой бетоном и арматурой. В общем случае, необходимо рассматривать следующие наклонные сечения, каждое из которых может оказаться наиболее слабым из условия восприятия поперечной силы (рис. 3.19):

идущие от внутренней грани опорных частей к точкам приложения сосредоточенных сил (линия 1), к концам отогнутых стержней (линия 2), к местам изменения шага хомутов от s1 до s2 (линия 3) или толщины стенки (линия 4);

идущие от начала отгибов к точкам приложения сосредоточенных сил (линия 5), к концам отгибов (линия 6), к месту изменения толщины стенки (линия 7).

Для наглядности отгибы и хомуты, а также соответствующие им наклонные сечения, на рис. 3.19 показаны в виде отдельных схем.

Для каждого из указанных сечений будет своя длина проекции e, конкретное число пересекаемых отогнутых стержней и хомутов.

                          а)

                                              

                                   б)

                                              

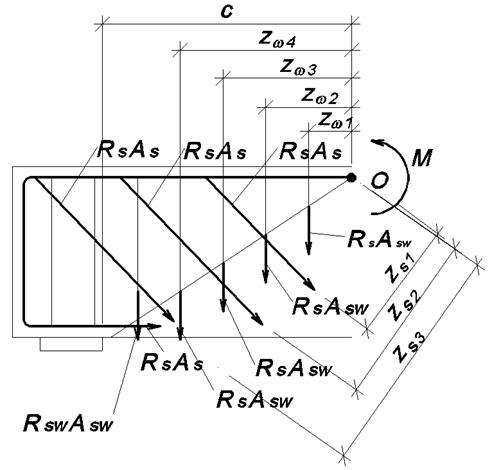
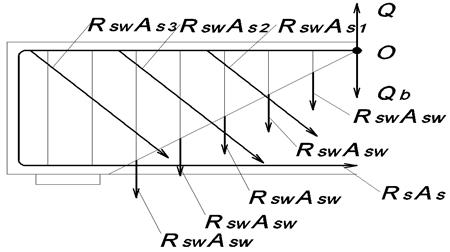
Рис. 3.18. Схемы для проверки прочности наклонного  сечения:

а) – на действие поперечной силы; б) – на действие изгибающего момента

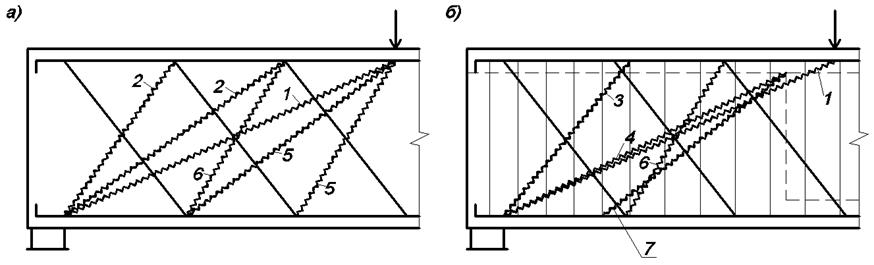
Рис. 3.19.   Возможные расположения наиболее опасных наклонных сечений:

а – при постоянной толщине стенки; б – при переменной толщине стенки

Нормы проектирования на участке длиной 2h₀ рекомендуют делать проверку наклонных сечений, проведенных под углом 45⁰ к вертикальному сечению.

Конец наклонного сечения во всех случаях должен находиться в центре сжатой зоны бетона. Высоту сжатой зоны бетона, измеряемую по нормали к продольной оси балки, можно определить из условия равенства проекций усилий в бетоне сжатой зоны и усилий в арматуре на продольную ось балки, при этом напряжения в бетоне сжатой зоны принимают равным его расчетному сопротивлению:

,                                             (3.57)

где  - угол наклона отогнутого стержня к горизонтали.

                  Из равенства (3.57) определяют площадь сжатой зоны , а затем ее высоту и положение центра тяжести. Полученная высота сжатой зоны должна быть не менее , в противном случае, арматуру  не учитывают.

                  Не будет большой ошибки, если центр тяжести сжатой зоны принимать в середине плиты.

                  Условие прочности (3.50), при выполнении которого исключается разрушение балки по наклонному сечению по рис.3.17,в, в развернутом виде:

,                                                          (3.58)

                  Величину коэффициента , учитывающего влияние хомутов на прочность стенки, подсчитывают по формуле:

,                                                                     (3.59)

где             - эмпирический коэффициент, принимаемый равным 5 при хомутах, нормальных к продольной балке, и равным 10 при наклонах под углом 45⁰ (при промежуточных углах наклона хомутов, величину  принимают по интерполяции);            n₁ – отношение модуля упругости арматуры к модулю упругости бетона (n₁=E_s/E_b); ;  - площадь сечения всех ветвей хомутов, расположенных в одной плоскости;  - шаг хомутов (расстояние между хомутами по нормали к ним); b – толщина стенки (ребра).

                  При расположении хомутов перпендикулярно к продольной оси балки коэффициент  должен быть не более 1,3.

                  Коэффициент , зависит от прочности бетона, его принимают  равным 1-0,01R_b.

                  Прочность наклонного сечения на действие изгибающего момента будет обеспечена при выполнении условия:

                                                                                                                             (3.60)

          Для исключения разрушения балки по схеме рис.3.17,б должно выполняться условие:

,                                                         (3.61)

где M – момент всех внешних сил, расположенных по одну сторону сечения, относительно оси, проходящей через центр тяжести площади сжатой зоны бетона в конце наклонного сечения;   - соответственно моменты, которые могут быть восприняты продольной арматурой, хомутами, отгибами.

                  Принято, что при разрушении от действия изгибающего момента полностью используется прочность всей арматуры (кроме продольной арматуры сеток, которую в расчете не учитывают). Условие прочности (3.61) при этом принимает вид (рис.3.19,б):

,                                             (3.62)

где z_s – расстояние от центра тяжести площади продольной арматуры до центра тяжести площади сжатой зоны бетона;  - то же для хомутов одной плоскости; z_i – то же для одного отгиба продольной арматуры.

                  Высоту сжатой зоны наклонного сечения, измеряемую по нормли к продольной оси балки и центр тяжести сжатой зоны определяют исходя из условия (3.57). Но с достаточной для практических целей точностью можно принять, что центр сжатой зоны, как и в расчете прочности наклонного сечения на действия поперечной силы, находится в середине высоты плиты.