Регулярное отношение предпочтения, предельная норма замены благ

Микроэкономика 9. Регулярное отношение предпочтения. Определение и свойства. Невыпуклые отношения предпочтения. Предельная норма замены благ. Взаимосвязь между предельной нормой замены благ и свойствами кривой безразличия.

Источник: лекции Ю.В. Федотова «Микроэкономика-2»

Определенное на множестве наборов благ (товаров) Rⁿ⁺ отношение предпочтения «не хуже, чем» ˆ называется рациональным, если оно является:

§  полным

§  рефлексивным

§  транзитивным

Рациональное отношение предпочтения является регулярным (“well-behaved”), если оно:

§  монотонно

§  выпукло.

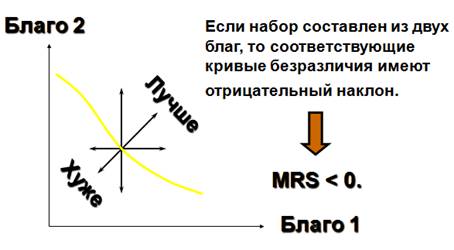
Монотонность: Большее количество блага всегда предпочитается меньшему, т.е. все наборы состоят только из благ (отсутствует насыщение).

Слабая (нестрогая) монотонность:

§  отношение предпочтения слабо монотонно, если для любых двух наборов благ x,y`Rⁿ⁺ таких , что x m y (x_i ³ y_i, iÎ1:n) выполняется x ˆ y.

§  отношение предпочтения слабо монотонно, если для любых двух наборов благ x,y`Rⁿ⁺ таких , что x ¨ y (x_i > y_i, iÎ1:n) выполняется x ˆ y.

Строгая монотонность: Отношение предпочтения строго монотонно, если для любых двух наборов благ x,y`Rⁿ⁺ таких , что x m y и xgy  выполняется соотношение x n y.

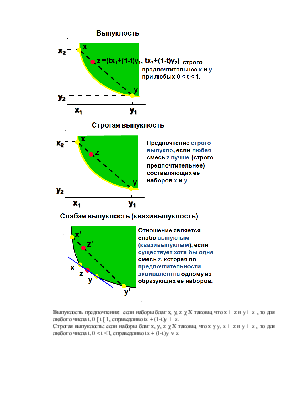
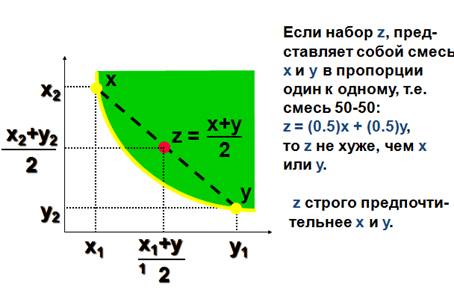
Выпуклость: Выпуклая комбинация двух различных, но при этом одинаково предпочтительных, наборов предпочтительнее или, по крайней мере, не хуже, чем каждый из составляющих ее наборов.

Выпуклость: Смесь одинаково предпочтительных наборов благ предпочтительнее (по крайней мере, слабо), чем любой из составляющих ее наборов. Например, смесь наборов x и y в пропорции 1 к 1 (или 50 на 50 в процентах) представляет собой набор z = (0.5)x + (0.5)y.
Набор z по крайней мере не хуже, чем x или y.

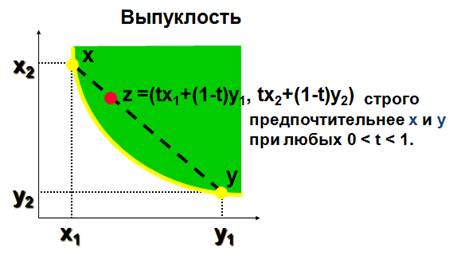
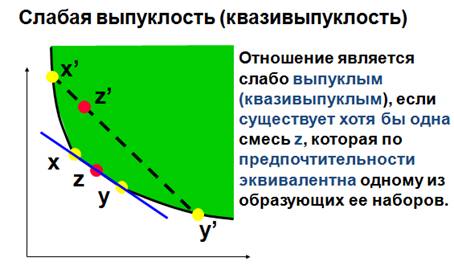
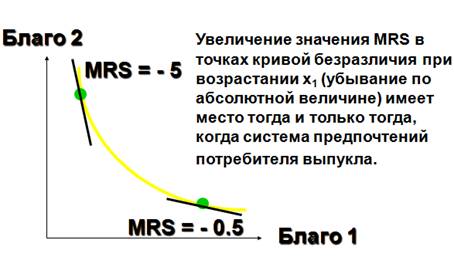
Выпуклость предпочтения:  если наборы благ x, y, z c X таковы, что x ˆ z и y ˆ z , то для любого числа t, 0 [ t [ 1, справедливо tx + (1-t)y  ˆ z.

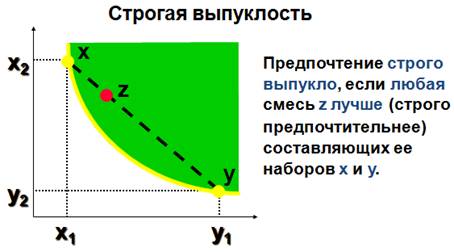
Строгая выпуклость: если наборы благ x, y, z c X таковы, что x g y, x ˆ z и y ˆ z , то для любого числа t, 0 < t <1, справедливо tx + (1-t)y  n z.

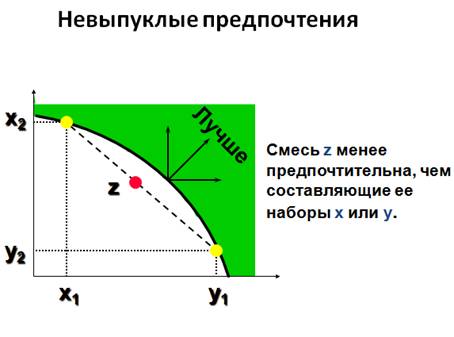
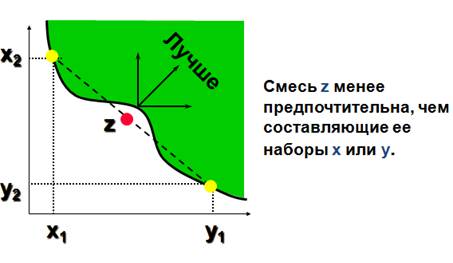
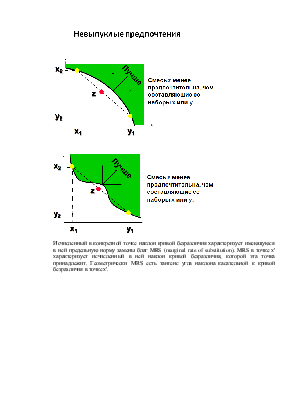
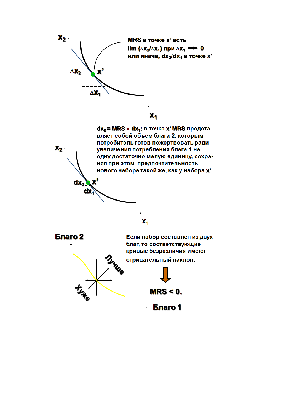
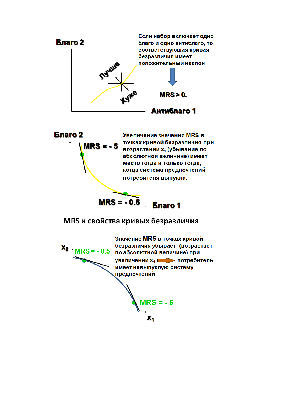
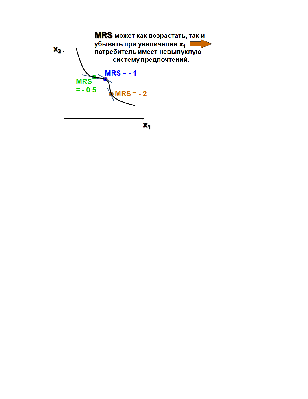
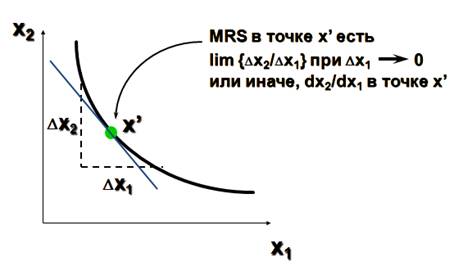
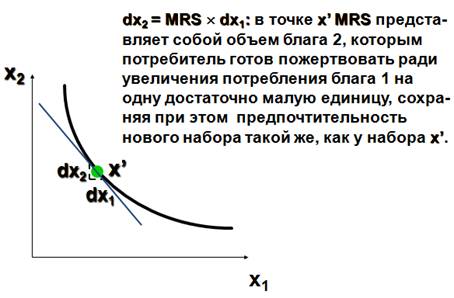
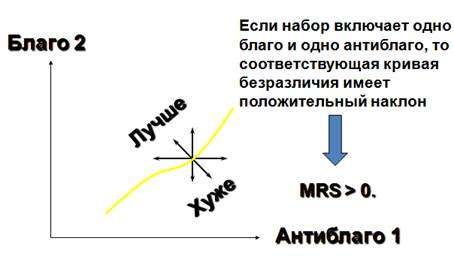
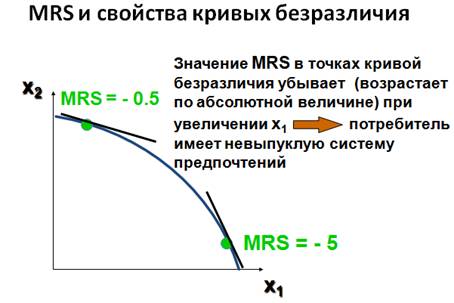
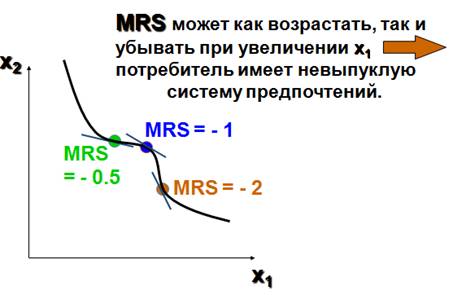
Исчисленный в конкретной точке наклон кривой безразличия характеризует имеющуюся в ней предельную норму замены благ MRS (marginal rate of substitution). MRS в точке x' характеризует исчисленный в ней наклон кривой безразличия, которой эта точка принадлежит. Геометрически MRS есть тангенс угла наклона касательной к кривой безразличия в точке x'.