



Тема:Нескінченно-спадаюча геометрична прогресія із
знаменником ![]()
Виклад нового матеріалу
На попередніх заняттях , ми одержали формулу суми n-перших членів геометричної прогресії, в якій ![]() .
Вона має такий вигляд:
.
Вона має такий вигляд:
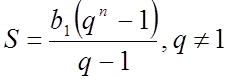
Сьогодні на уроці
ми дізнаємось як знайти суму нескінченно-спадної геометричної прогресії при ![]() <1
<1
Візьмемо довжину відрізка АВ рівну двом одиницям
При цьому візьмемо т.![]() — середину відрізка АВ, потім т.
— середину відрізка АВ, потім т.![]() — середину
— середину![]() ,
потім т.
,
потім т. ![]() —середину
—середину ![]() і
так далі.
і
так далі.
Розглядаючи даний малюнок, ми можемо зробити деякі висновки, а саме:
![]() =1;
=1;
![]() =
=![]() ;
;
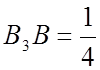 ,
і так далі.
,
і так далі.
Тобто
довжини відрізків ![]() і так далі утворюють нескінченну геометричну
прогресію знаменник якої рівний
і так далі утворюють нескінченну геометричну
прогресію знаменник якої рівний ![]() :
:
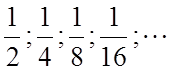
Знайдемо суму n-перших членів цієї прогресії:
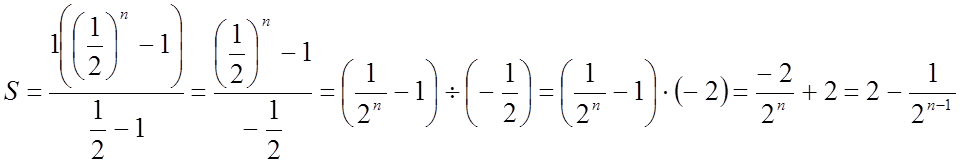
Глянемо на дріб 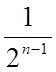 , при збільшенні
числа доданків n значення
дробу прямує до нуля.
, при збільшенні
числа доданків n значення
дробу прямує до нуля.
Наприклад: якщо n=20, то 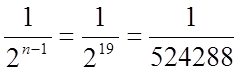
Тобто число вже на даний момент дуже маленьке, а якщо
взяти n=100, або n=1000, то практично даний дріб буде рівний нулю.Тому при
необмеженому збільшенні n різниця 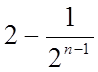 становиться як
завгодно близьким до 2 або, як кажуть, наближається до 2.
становиться як
завгодно близьким до 2 або, як кажуть, наближається до 2.
Таким чином:сума n первих членів геометричної прогресії 1;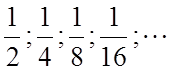 при необмеженому збільшенню n прямує до числа 2.
при необмеженому збільшенню n прямує до числа 2.
Число 2
називають сумою нескінченної геометричної прогресії 1;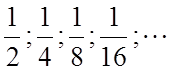 і записують:
і записують:
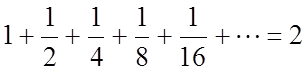
Якщо цю рівність пояснити геометрично, томи переконуємось що сума
довжин відрізків ![]() … дорівнює довжині відрізка АВ.
… дорівнює довжині відрізка АВ.
Візьмемо
тепер довільну геометричну прогресію: ![]() …
у якої
…
у якої ![]() .
.
Візьмемо вже знайому нам формулу суми n первих членів прогресії:
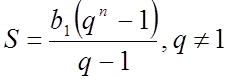
Перетворимо праву частину рівності:
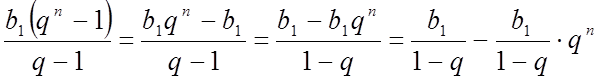
Можна довести що,
якщо ![]() , то
при необмеженому збільшенні n множник
, то
при необмеженому збільшенні n множник ![]() прямує до нуля, значить прямує до нуля і дріб
прямує до нуля, значить прямує до нуля і дріб 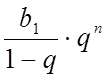 .При цьому сума
.При цьому сума ![]() прямує до
числа
прямує до
числа 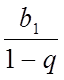 .Число
.Число 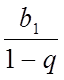 називають сумою нескінченної геометричної прогресії
називають сумою нескінченної геометричної прогресії![]() , у якої
, у якої![]() .
.
Це записують так:
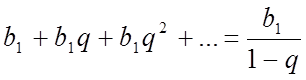
Позначивши суму прогресії ![]() буквою S , одержимо
формулу
буквою S , одержимо
формулу 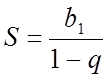 .
.
Приклад: Знайдемо суму нескінченної геометричної прогресії:
15; -3; ![]() ;…
;…
В
даному випадку 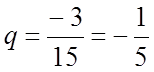 , значить умова
, значить умова ![]() виконується:
виконується:
За
формулою одержімо: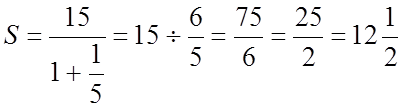
Відповідь: ![]() .
.
Нам
відомо, що кожне раціональне число ![]() , де m – ціле число, а n – натуральне, можна
подати у вигляді нескінченного дисятичного дробу, шляхом ділення чисельника на
знаменник.
, де m – ціле число, а n – натуральне, можна
подати у вигляді нескінченного дисятичного дробу, шляхом ділення чисельника на
знаменник.
Покажемо на прикладі, як з допомогою формули суми
нескінченної геометричної прогресії можна подати нескінченний десятичний
періодичний дріб у вигляді відношення ![]() .
.
Приклад: Представити
нескінченний дисятковий періодичний дріб ![]() у
вигляді звичайного дробу.
у
вигляді звичайного дробу.
Представимо дріб ![]() у вигляді суми:
у вигляді суми:
![]() =0.18+0.0018+0.000018+…
=0.18+0.0018+0.000018+…
Доданки в правій частині
рівності — члени геометричної прогресії, у якої перший член рівний 0,11, а
знаменник рівний 0,001 ,тобто умова ![]() виконується.
Знайдемо суму цієї прогресії:
виконується.
Знайдемо суму цієї прогресії:
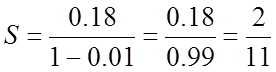 .
.
Домашнє завдання
№ 420 (б; є)
1)
Перевірити , що ![]() ,і якщо це так знайти суму:
,і якщо це так знайти суму:
б) 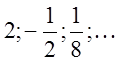
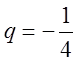 , тоді
, тоді 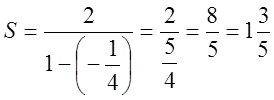
Відповідь:![]() .
.
е) 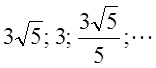
q=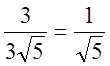
![]()
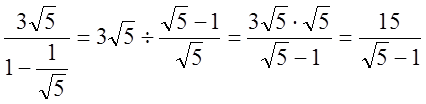
Відповідь: ![]()
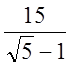 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.