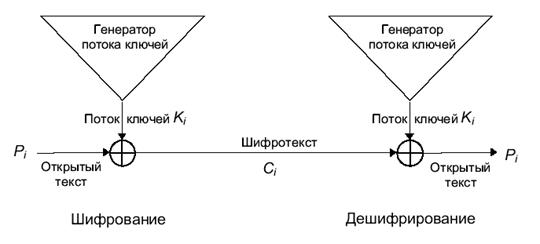
Надежность системы
шифрования целиком зависит от генератора гаммы. Если генератор гаммы создает
бесконечную строку нулей, то шифртекст полностью совпадает с открытым текстом,
и операция становится бессмысленной. Если генератор гаммы выдает повторяющийся
16-битовый фрагмент, защита ничтожно мала. Если же генератор гаммы создает
бесконечный поток истинно случайных битов, мы получает
шифр с совершенной защитой. Фактически генератор
Рис.2.6. Схема потокового шифра гаммы создает битовый поток, который должен быть безошибочно воспроизведен при расшифровании, и поэтому не может быть истинно случайным. Стойкость шифра зависит от того, насколько гамма близка к истинно случайному потоку битов. Генератор гаммы при каждом запуске должен создавать разные битовые потоки. Если это не так, то при наличии фрагмента открытого текста взлом шифра тривиален. Поэтому во всех потоковых шифрах применяются ключи, и выход генератора гаммы определяется ключом.
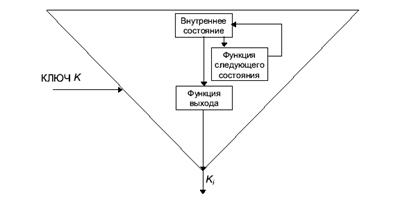Генератор гаммы состоит
из трех основных частей. Внутреннее состояние – это текущее состояние генератора
гаммы (его часто называют вектором инициализации, Initial Vector). Два генератора с
одинаковым ключом и одинаковым внутренним состоянием создают одинаковые гаммы.
Функция переходов считывает теку
щее внутреннее состояние и генерирует новое внутреннее состояние. Выходная функция считывает текущее внутреннее состояние и генерирует новое внутреннее состояние. Поскольку генератор
Рис.2.7. Устройство генератора гаммы гаммы должен выдавать одинаковую гамму как на стороне передатчика, так и на стороне приемника, выход генератора является строго детерминированным, и имеет конечную длину. Эта длина последовательности генерируемых битов называется периодом генератора гаммы (поскольку после этого последовательность битов в точности повторяется). Для того, чтобы шифрование было достаточно надежным, период генератора гаммы должен намного превышать число битов, генерируемых между заменами ключей. Если период окажется меньше размера открытого текста, различные части открытого текста будут зашифрованы одинаково. Это значительно снижает надежность системы шифрования.
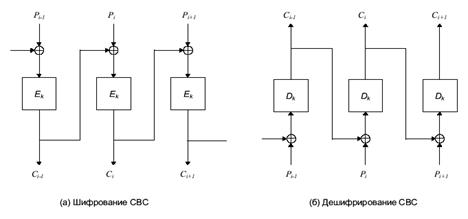
В режиме сцепления блоков (Cipher Block Chaining, CBC) каждый блок используется для модифицирования шифрования следующего блока. Таким образом, каждый блок шифртекста зависит не только от шифруемого блока открытого текста, но и от всех предыдущих блоков открытого текста.
В режиме сцепления блоков перед шифрованием очередного блока выполняется операция XOR над открытым текстом и предыдущим блоком шифртекста. Когда очередной блок зашифрован, результат шифрования сохраняется в специальном регистре. Следующий блок открытого текста перед шифрованием подвергается операции XOR с содержимым регистра. Полученный результат снова сохраняется в регистре, и так до конца сообщения. Таким образом, шифрование каждого блока зависит от всех предыдущих блоков.
.
8 Функция хэширования (или хэш-функция, хэш-код) - это однонаправленная
функция, которая, получив сообщение М произвольной длины в качестве аргумента,
возвращает значение хэш-код Н(М) фиксированной длины: 
, где H имеет длину m.
Другие названия хэш-функций: функции сжатия, функции свертки, криптографическая контрольная сумма. Хэш-код является функцией всех битов сообщения, и обеспечивает возможность контроля ошибок: изменение любого числа битов в сообщении приводит к изменению хэш-кода, причем при незначительном изменении исходного сообщения значение хэш-кода меняется очень сильно.
Хэш-функции можно разделить на два класса: Бесключевые – на их вход подается только сообщение; Ключевые – на их вход подается сообщение и секретный ключ.
Бесключевые хэш-функции еще называют кодами обнаружения изменений в сообщении (MDC-код, modificationdetectioncode). Они являются составными элементами цифровых подписей. Бесключевые хэш-функции помогают обеспечить целостность сообщения (совместно с другими механизмами).
К ключевым хэш-функциям относятся коды аутентичности сообщений (МАС-коды). Они предназначены для обеспечения целостности данных и аутентификации сообщений без использования каких-либо других механизмов.
Требования, предъявляемые к функциям хэширования:
· Хэш-функция должна выполнять функцию сжатия, т.е. отображать строку сообщения М произвольной длины в строку h=H(M) фиксированной длины m.
· Легкость вычисления h=H(M) при известном М
К ключевым хэш-функциям дополнительно предъявляется требование:
· Стойкость к вычислению. Оно означает, что по известной паре «текст-МАС-код»
(M,H(M)) невозможно вычислить любую другую пару
«текст-МАС-код» 
для любого нового текста 
без знания секретного ключа.
К бесключевым хэш-функциям дополнительно предъявляются требования:
· Функция должна быть однонаправленной, т.е. значение хэш-функции Н(М) должно вычисляться легко, но по ее значению должно быть практически невозможно вычислить исходное сообщение М. Это свойство называется односторонностью (one-way), или стойкостью к прообразу (preimageresistance).
· Функция должна быть устойчива к коллизиям (collisionresistance). Это значит, что должно быть практически невозможно найти два разных сообщения M и М1, для которых H(M)=H(M1).
Основной способ построения хэш-функций – использование сжимающих функций, для которых входными данными являются блок сообщения и выходные данные от предыдущих блоков текста, т.е. hi = f(Mi, Hi-1)
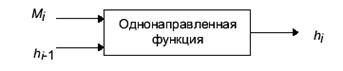Рис.2.12.
Общая схема вычисления хэш-функции.
Функция хэширования применяется следующим образом. Отправитель вычисляет функцию хэширования и присоединяет ее к своему сообщению. Получатель устанавливает аутентичность сообщения путем повторного вычисления функции хэширования и сравнения полученного значения с тем, которое передано с сообщением. Поскольку сама функция хэширования не считается секретной, при передаче необходимы средства для защиты ее значения.
Алгоритм MD5 – это улучшенная версия алгоритма MD4. Алгоритм берет в качестве входных данных сообщение произвольной длины и выдает на выходе хэш-код размером 128 бит. Вводимые данные обрабатываются последовательно 512-битовыми блоками. Алгоритм включает следующие этапы:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.