Другие предметы \ Надёжность систем автоматизации

Определение показателей надёжности управления системой каутизации щелков, страница 2

Наименование элементов

Позиция по схеме

Количество элементов i-го типа

Интенсивность отказов,

ч-1

Кнопочный переключатель

SB1,SB2,SB3,SB4,

SB5

5

0,7

3,5

Соединения жесткие

58

0,6

34,8

Арматура сигнальная

HL1,HL2,HL3,HL4,

4

0,71

2,48

Пускатель магнитный

  -катушка

  -контакты

КМ1,КМ2,KL

3

            9

0,04

0,3

0,12

2,8

Провода соединительные

100м

0,015

1,5

Тепловое реле

КК

2

0,3

0,6

Предохранитель плавкий

FU

1

0,5

0,5

Поворотный переключатель

SA

5

0,175

0,875

Контакт уровнемера

L

1

42

42

По интенсивностям отказов (таблица 1) определим основные показатели надёжности, используя соотношения количественных характеристик экспоненциального закона:

а) суммарная интенсивность отказов:

                       

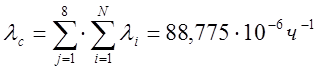
б) средняя наработка до первого отказа:

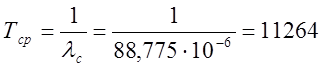                        ч.

в) вероятность безотказной работы в течении определённого промежутка времени (t=2000, 4000, 6000, 8000, 10000, 11264 ч):

                         P(t)=,

 P(2000)=;

 P(4000)=;

 P(6000)=;

 P(8000)=;

 P(10000)=.

P(11264)=.


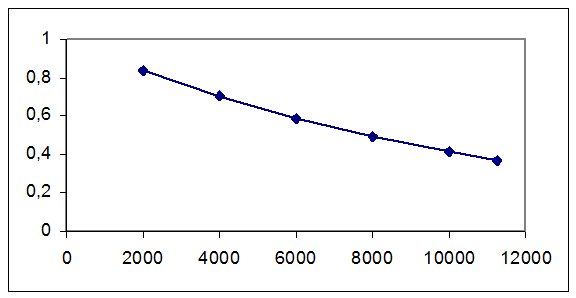По рассчитанным данным строим график зависимости P(t)  от времени (рисунок 4).

Рисунок 4-Вероятность безотказной работы

г) Вероятность отказов в течении определённого промежутка времени (t=2000, 4000, 6000, 8000, 10000, 11264 ч):

                        Q(t)=1-P(t),

Q(2000)=1-0,8373=0,1627;

Q(4000)=1-0,7011=0,2989;

Q(6000)=1-0,587=0,413;

Q(8000)=1-0,4915=0,5085;

Q(10000)=1-0,4116=0,5884,

Q(11264)=1-0,3679=0,6321,


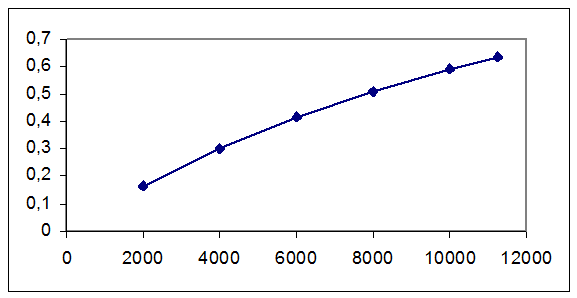По рассчитанным данным  строим график зависимости Q(t) от времени (рисунок 5).           

Рисунок 5-Вероятность отказов

д) Частота отказов в течении определённого промежутка времени (t=2000, 4000, 6000, 8000, 10000, 11264 ч):

                             а(t)=,

                             а(t)=88,775*10-6*0,8373=74,3313*10-6;

                             a(t)=88,775*10-6*0,7011=62,2402*10-6;

                             a(t)=88,775*10-6*0,587=52,1109*10-6;

                             a(t)=88,775*10-6*0,4915=43,6329*10-6;

                             a(t)=88,775*10-6*0,4116=36,5398*10-6.

                             a(t)=88,775*10-6*0,3679=32,6603*10-6.

По рассчитанным  данным  строим график зависимости а(t) от времени (рисунок 6).                        


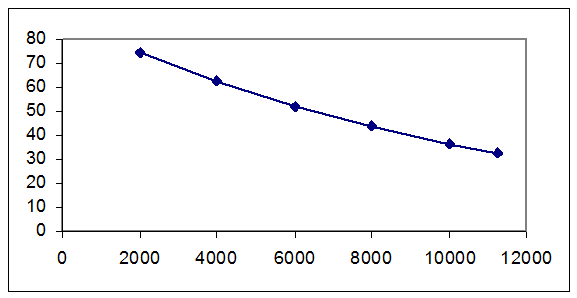Рисунок 6-Частота отказов

е) Интенсивность отказов за время t (t=2000, 4000, 6000, 8000, 10000, 11264ч):

                                   ,

                                    ;

                                    ;

                                    ;

                                    ;

                                    ;

                                    .

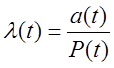По рассчитанным  данным  строим график зависимости (t) от времени (рисунок 7).                       


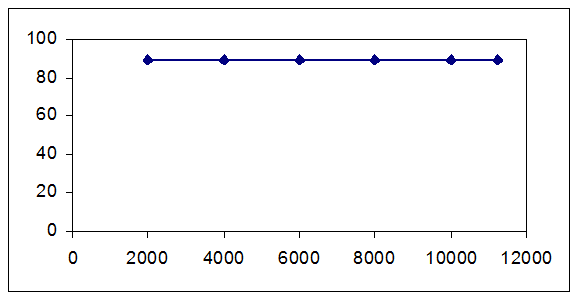Рисунок 7-Интенсивность отказов

Преобразовываем принципиальную электрическую схему управления (рисунок 3) в структурную схему надёжности (рисунок 8). Находим интенсивность отказов всей системы, используя формулы для параллельного и последовательного соединения элементов. В процессе преобразования схемы переходим к промежуточной форме (рисунок 9,10), а затем к окончательной форме (рисунок 11).

Рисунок 8-Структурная схема надёжности

Определим вероятность безотказной работы Р(t) для каждого элемента схемы при t=1000 ч.

 Р(1000)=,

Р1=            Р2=               Р3=

Р4=            Р5=            Р6=

Р7=            Р8=             Р9=   

Р10=          Р11=           Р12=

Р13=       Р14=             Р15=

Р16=          Р17=           Р18=

Р19=          Р20=           Р21=    

Р22=       Р23=           Р24=        

Р25=          Р26=          Р27=        

Р28=          Р29=          Р30=

Определим Р(t) для звеньев промежуточной схемы надёжности.

Рисунок 9-Промежуточная структурная схема надёжности

Р30=Р1*Р2=0,9995*0,9993=0,9988

Р31=P3*(1-(1-Р4)*(1-Р7))=0,99998

Р32=Р5*Р6=0,9997

Р33=P8*(1-(1-Р9)*(1-Р10))=0,9998

Р34=Р11*Р12=0,9995

Р35= P13*(1-(1-Р14)*(1-Р17))=0,9998

        Р36=Р15*Р16=0,9997

Р37= P18*(1-(1-Р19)*(1-Р20))=0,9998

Р38=Р21*Р22=0,9587

Р39=Р23*Р24=0,999

Р40=Р25*Р26=0,999

Р41=Р27*Р28=0,999

Р42=Р29*Р30=0,999

Рисунок 10-Промежуточная структурная схема надёжности

Р43=P32*(1-(1-Р31)*(1-(1-Р33)(1-Р34)))=0,9997

Р44=P36*(1-(1-Р35)*(1-Р37))=0,9997

Определяем Р(t) для всей структурной схемы надёжности.

 


Рисунок 10-Окончательная структурная схема

Рс=Р30*(1-(1-Р43)*(1-Р44)*(1-Р38)*(1-Р39)*(1-Р40)*(1-Р41)*(1-Р42))=0,9988

Так как Рс>0,8 то можно сделать вывод, что система удовлетворяет требованиям технологии.

1.3  Структурно-логический анализ системы.

Анализируя структурную схему, можно определить при отказе каких элементов схема выйдет из строя или потеряет частично свою работоспособность.

При отказе звеньев Р1 и Р2 произойдёт отказ всей системы, так как этими элементами являются соответственно предохранитель, который соединяет электрическую сеть с данной электрической схемой и кнопка отключения всей схемы.

При отказе других составных элементов структурной схемы произойдёт лишь частичный отказ схемы либо их отказ не окажет существенного влияния на работоспособность системы.

Заключение

В расчётно-графической работе произведены расчёт параметров надёжности системы регулирования температуры конденсата в баке, а также расчёт параметров надёжности для системы управления ленточного конвейера и насоса. Составлены структурная схема надёжности функциональной схемы регулирования и структурная схема надёжности принципиальной электрической схемы управления. Построены зависимости показателей надёжности от времени.

Список использованных источников

1. Шувалов В.В., Огаджанов Г.А., Голубятников В.А. Автоматизация производственных процессов в химической промышленности. –М.:Химия, 1991.-480с. 

 

Скачать файл