Технологическое программирование регулирующего микроконтроллера

Содержание

Введение

1.  Выбор модификации

2.  Размещение алгоритмов по алгоблокам

2.1   Назначение и описание применяемых алгоритмов

2.2   Схема размещения алгоритмов по блокам

2.3   Процедура «Алгоритм»

3.  Технологическая программа

3.1 Блок-схема взаимосвязей алгоблоков в соответствии со          структурой решаемой задачи

3.2   Таблица технологической программы 3.3   Процедура конфигурирования

4.  Настройка параметров алгоблоков

5.  Начальные условия

6.  Параметры приборов

7.  Параметры системы

8.  Ресурсы, требуемые алгоблокам

9.  Расчет сопло-заслонка

Задание № 1

1.  Локальное аналоговые  ПИД – регулирование одного параметра  объекта N2, N3, N4 (X2ан, X3ан,X4ан).

2.  Сигналу на соответствующем  контроллере выхода каждого регулируемого параметра объекта N2, N3, N4 за пределы  ограничений.

3.  Индикацию на лицевой панели контроллера N1 номера любого из объектов (N2, N3, N4), где аналоговый сигнал вышел за пределы ограничений, передачу этого номера на лицевую панель контроллера N3 .

4.   Возможность индикации состояния заданной логической функции  Y=f(x1,x2,x3,x4)      дискретных сигналов контроллеров N1, N2, N3, N4  на лицевой панели контроллера N2

Спроектировать распределенную систему управления четырьмя объектами на каждом из которых установлен контроллер «Ремиконт – 130»

Таблица №1

№	Свободные алгоблоки	Цепи типа А		Цепи типа Б
		Nвх алгоблока Аналог. ввода	Nвых алгоблока Аналог. вывода	Nвх алгоблока дискр. ввода	Nвых алгоблока Дискр. Вывода
1	1-10,  11-25	1-4	1	1-4	1-4

1.Выбор модификации

Выбор модификации ведем по данным к заданию, выбирая  модификацию по Приложению 1

Контроллер № 1:

Так как у нас нет аналоговых входов и выходов,  то модификацию ведём по дискретным входам и выходам. В данном случае у нас 1 вход. Значит, выбираем модификацию 70.

Контроллер № 2:

Так как у нас есть аналоговые входы и выходы и дискретные входы,  то модификацию ведём по дискретным входам и аналоговым входам и выходам. В данном случае у нас 5 входов и 2 выхода аналоговых и 1 вход дискретный. Отсюда, выбираем модификацию 17.

Контроллеры № 3, № 4:

Выбираем модификацию такую же как и у контроллера № 2

2. Размещение алгоритмов по алгоблокам

2.1 Назначение и описание применяемых алгоритмов

            При проектировании данной распределительной системы были использованы следующие алгоритмы: ОКО,  РЕГА, ВИН, ИНВ, ВДБ, ДВБ, ПОК, МИЛ, МНИ .

            Описание и назначение каждого алгоритма приведены ниже (Приложение 4)

Минимизация логической функции

            В соответствии с заданием дискретные сигналы с объекта N1, N2, N3, N4 принимаются в контроллере N2 и поступают на логическую схему 

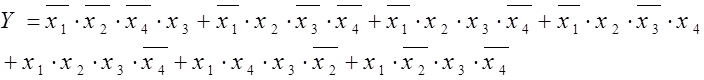
Данная формула громоздка, поэтому требует минимизации. Произведем минимизацию при помощи карты Карно. Комбинация переменных, при которых функция истинна, называют

минтермами. Представление логической функции в виде минтермов определяет ее СДНФ:

				X2
						x1
x4
x3

    Минтермы минимизируемой функции отмечаются  «1» в соответствующих клетках карты.

  Минимизацию необходимо проводить по следующим правилам:

1.  Из единиц образуем правильные контуры. Контур считается правильным, если он имеет прямоугольную форму и содержит 2ⁿ клеток.

2.  В контур должны входить только соседние клетки, т.е. стоящие рядом или на противоположных сторонах карты.

3.  Контуры могут накладываться друг на друга. Требуется образовать минимальное число контуров с максимальным количеством клеток в них.

4.  Записываем элементарные конъюнкции для каждого контура. Переменная входит в выражение (конъюнкцию) без инверсии, если соответствующая скобка полностью охватывает контур, с инверсией, если полностью не охватывает, и вообще не входит в выражение, если охватывает частично.

В соответствии с правилами составим карту Карно для заданной функции, и минимизируем ее.

				x2
						X1
			0	1	0	0
x4			1	0	0	1
			1	0	0	1
x3			0	1	1	0

Получаем три  контура, которые записываем в элементарные дизъюнкции:

 Y = x₄ x₂+ x₂ x₄ x₁ + x₂ x₃ x₄

Получаем  четыре  контура, которые записываем  в элементарные конъюнкции:

Y = ( x₂ + x₄ )( x₁ + x₂ + x₃ )( x₄ + x₂ )

Реализуем  эти формулы при помощи алгоритмов логических функций, которые называются  МИЛ, МНИ. Описание  этих алгоритмов  приведено ниже  (Приложении 2)

	МИЛ
X2 X2		01 02         01
	МИЛ				МНИ
X1 X2 X4		01 02         01 03				01 02         01 03
	МИЛ
X2 X3 X4		01 02         01       03

Рис.1  Реализация  логической функции  ДНФ

	МНИ
X2 X4			01 02         01
	МНИ						МИЛ
X1 X2 X3			01 02         01 03					01 02         01 03
	МНИ
X2 X4		01 02         01

Рис.2  Реализация  логической функции  КНФ

Расчитываем  требуемые ресурсы  для  реализации логических функций КНФ и ДНФ