- достоинства – главным достоинством является опыт, руководствуясь которым специалист без проблем определяет предпочтительные варианты.
Достоинства компьютера, как математического аппарата, являются недостатками человека и наоборот, недостатки человека являются достоинствами компьютера. Человек испытывает трудности для реализации математического аппарата и это занимает немало времени, спустя которое может измениться ситуация на рынке. При компьютерном выборе без специалиста велика вероятность использования неактуальных показателей эффективности или неверно наложенных ограничений на тип ”совместимость”.
Следовательно, нашей задачей является синтез компьютерной памяти, разрядности и человеческого опыта, и трезвой мысли. Только такой синтез позволяет извлечь из оптимизации выбора экономический эффект.
1 Постановка задачи
Прежде чем приступать к написанию программы нужно проанализировать ситуацию на рынке программного обеспечения. На рынке программного обеспечения, программ такого типа нет.
Перспективным для реализации поставленной задачи является использование приложений Acsess и Excel из пакета MS-Office с написанием соответствующих макросов. Acsess является реляционной базой данных.
Реляционные системы далеко не сразу получили широкое распространение. В то время, как основные теоретические результаты в этой области были получены еще в 70-х, и тогда же появились первые прототипы реляционных СУБД, долгое время считалось невозможным добиться эффективной реализации таких систем.
К числу достоинств реляционного подхода можно отнести:
а) наличие небольшого набора абстракций, которые позволяют сравнительно просто моделировать большую часть распространенных предметных областей и допускают точные формальные определения, оставаясь интуитивно понятными;
б) наличие простого и в то же время мощного математического аппарата, опирающегося главным образом на теорию множеств и математическую логику и обеспечивающего теоретический базис реляционного подхода к организации баз данных;
в) возможность ненавигационного манипулирования данными без необходимости знания конкретной физической организации баз данных во внешней памяти.
Отмеченные выше преимущества и постепенное накопление методов и алгоритмов организации реляционных баз данных и управления ими привели к тому, что уже в середине 80-х годов реляционные системы практически вытеснили с мирового рынка ранние СУБД.
Основным достоинством реляционной базы данных является использование теории множеств, которая позволяет наглядно манипулировать данными.
При работе с поздними моделями данных, таких как иерархическая и сетевая, возникают следующие проблемы:
а) сложность пользования;
в) необходимы знания физической организации;
г) зависимость прикладных систем от физической организации;
д) логика перегружена деталями организации доступа к БД.
В нашем случае данные представлены в виде таблицы, что при выборе реляционной модели данных упрощает разработку и использование программного обеспечения. В настоящее время, подавляющее большинство разработанных баз данных используют реляционную модель представления данных. Наработан большой банк данных, и чтобы использовать эти данные для своих целей желательно придерживаться реляционной модели.
2 Анализ методов оптимального выбора
Предлагаемая последовательность выделения оптимального варианта из конечного множества сравниваемых состоит из следующих этапов [1]:
- формирование исходного множества;
- формирование допустимого множества;
- формирование множества не худших вариантов;
- выбор оптимального варианта.
Отметим, что данная последовательность включает в себя все стандартные необходимые действия, необходимые для выбора лучшего варианта с использованием языка бинарных отношений, что позволяет существенно упростить процедуру принятия решения и снизить при этом степень произвола до достаточного минимума. Описание методов оптимального выбора: лексикографического и с последовательными уступками приведен в [1].
2.1 Метод идеальной точки
Метод основан на применении принципа потенциального распределения вероятности [2]. Сущность метода – определение коэффициента соизмеримости на основе принципа потенциального распределения вероятностей.
Одним из обобщенных показателей эффективности является коэффициент соизмеримости образца, представляющий собой отношение эффективности рассматриваемого образца в условиях обеспечения технологии и эффективности некоторого заданного образца, принимаемого за эталонный. Целесообразно за эталонный принимать гипотетический образец с оптимальной совокупностью технических характеристик.
Наиболее подходящая схема решения этой задачи может быть построена на основе принципа потенциального распределения вероятности. Этот принцип отражает определенную модель поведения среды в условиях которой проявляются свойства системы.
Введем в рассмотрение показатели:
rji=xji/xjэ или (rji=xjэ/xji) (1)
Отражающие относительный уровень j-й технической характеристики i-го образца по сравнению с эталонным. Система показателей (2) выбирается таким образом, чтобы показатель был равен или меньше единицы в любом случае, т.е. если желательно j-ю характеристику увеличить, то применяют формулу (24) без скобок, если уменьшить, то в скобках.
Допустим, что существует объективная система оценок весов каждой характеристики Pj=(j=1,m). Из-за того что
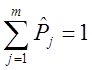 (2)
(2)
Принцип потенциального распределения постулирует применение для сравнения вариантов критерия Байеса:
bi=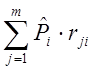 (3)
(3)
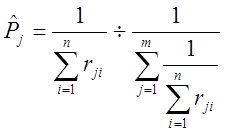 (4)
(4)
Можно показать, что эта оценка в соответствии с принципом максимализма неопределенности может быть получена в результате решения следующей задачи на условный экстремум:
H=-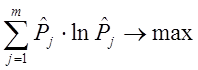 (5)
(5)
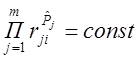 (6)
(6)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.