Модели и методы анализа и оптимизации технологических циклов управления космических аппаратов

  1.2.        Модели реализуемости ТЦУ

Рассмотрим подробно модели и методы анализа и оптимизации ТЦУ КА, которые используются в рамках представленной выше аналитико-оптимизационной процедуры и позволяют получать как аналитические, так и вероятностные характеристики процессов управления КА.

1.2.1.     Анализ реализуемости детерминированных моделей

Поскольку описание технологических циклов управления не зависит от типа комплекса управления,  имеется начальное значение вектора временной развертки для графа ТЦУ G

где t_i соответствует времени задействования компонента структуры ВС для решения задачи находящейся в i-ой вершине графа G. Вектор временной развертки полностью определяет информационное взаимодействие между структурными компонентами сети.

Граф технологического цикла управления G, построенный на этой структуре, описывается матрицей инцидентности A=a[i,j]. Это прямоугольная матрица размерности nxm, где

Также используется вектор реализации (ВР), который упоминался выше, 

где h _j является временем выполнения задачи обработки информации и управления ТЦУ, находящейся в начале j-ой дуги и задается структурой ВС.

Итак, при анализе реализуемости ТЦУ необходимо установить возможность реализации вектора временной развертки на ВС с заданной структурой при заданном векторе h.

Для реализации алгоритма анализа реализуемости ТЦУ сформулируем следующее утверждение.

Для реализации ТЦУ на заданной структуре ВС с заданным ВВР t необходимо и достаточно выполнение следующего условия: если из  i-ой вершины графа ТЦУ выходит j-ая дуга, входящая в n-ую вершину, то разница t_n-t_i должна быть не меньше, чем время выполнения задачи в i-ой вершине.

                                                                                                (1.1)

Итак, благодаря матрице A и векторам t и h становится возможным определение многих характеристик процесса выполнения ТЦУ. Например, время реализации определим по формуле:

                                                                                (1.2)

где z_i является временем выполнения задачи, реализация которой начинается  в момент t_i.

Отметим, что последовательность выполнения задач ТЦУ соответствует упорядочению координат ВВР по возрастанию. Если некоторые координаты равны, то это указывает на их параллельное выполнение.

Для случая, когда неравенство (1.1) не выполняется, предлагается следующий алгоритм коррекции ТЦУ, который позволяет производить замену компонентов ВВР на удовлетворительные. Для того, чтобы этот корректирующий алгоритм имел смысл, необходимо выполнение следующих условий.

1.  Условие неотрицательности

                                                                             (1.3)                                                                            

где I={i} это совокупность задач ТЦУ;

2.  Условие завершения предыдущих задач ТЦУ

                                                                      (1.4)

3.  Условие логической последовательности

                                                                   (1.5)

где a _ij - это коэффициент связности задач, т.е.

                   

t_i  и h_i  являются компонентами векторов ВВР и ВР соответственно.

Для каждой задачи ТЦУ введем параметры:

t_i^f - момент времени, до истечения которого ценность i-ой задачи остается максимальной.

t_i^s - момент времени, до истечения которого выполнение i-ой задачи невозможно.

                                                                                       (1.6)

Очевидно, что 

где T - длительность реализации ТЦУ.

Если условия (1.3)-(1.5) выполняются, то выполняются и условия 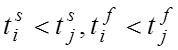 для связных задач i и j. С другой стороны, если ТЦУ существует, то:

               

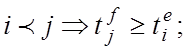
где  и  - моменты начала j-ой и завершения i-ой задач.

Поэтому, для каждой связной пары i и j замена при коррекции ВВР "старых" значений  на "новые" max и, соответственно,  на     min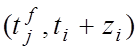 не влияет на факт допустимости существования ТЦУ. Таким образом, в результате работы алгоритма коррекции "старые" координаты ВВР меняются на "новые", удовлетворяющие следующим условиям.

1)         ;

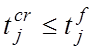2)  ;

3)  .

Итак, был подробно рассмотрен второй шаг аналитико- оптимизационной процедуры.