САР давления в химическом реакторе, страница 2

                                                                                    (2)

Д в и г а т е л ь  п о с т о я н н о г о  т о к а (ДПТ). В качестве двигателя постоянного тока возьмем двигатель МИ-11 [3], так как его мощность равна больше мощности, которая получается на его входе и состоит из произведения мощностей МП и усилителя.

Его характеристики:

-  Номинальное напряжение U_ном , В                                         110

-  Мощность двигателя Р_дв, кВт                                                   19

-  Ток якоря I_я, А                                                                         1,53

-  Частота n_дв, об/мин                                                                1500

-  Сопротивление якоря R_я, Ом                                                0,58

-  Номинальный момент М_ном, Н×м                                            6,25

-  Момент инерции J1, кг×м                                                        0,24

Проверим подходит ли выбранный двигатель:

проверим круговой частоте двигателя:

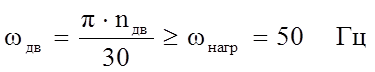
подставим значения и получим:

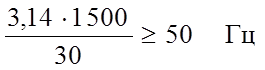
Вывод: данный двигатель подходит. Теперь найдем передаточную функцию ДПТ, согласно Топчееву [4] данная передаточная функция равна:

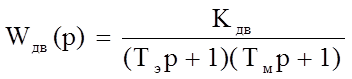                                                           (3)

где К_дв – коэффициент двигателя;

      Т_э – электрическая постоянная;

      Т_м – механическая постоянная.

Так как при расчетах Т_э очень малая величина, то первой скобкой можно пренебречь, тогда передаточная функция будет равна:

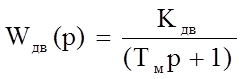                                                                         (4)

Найдем составляющие данного выражения из основных уравнений равновесия ДПТ:

1)  уравнение электрического равновесия:

                                                                  (5)

2)  уравнение механического равновесия:

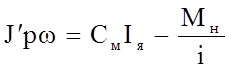                                                                           (6)

3)  уравнение зависимости угла поворота вала двигателя от угловой скорости:

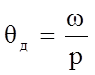                                                                                            (7)

После преобразований найдем:

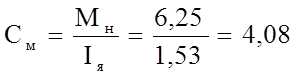
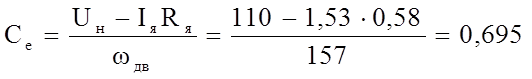
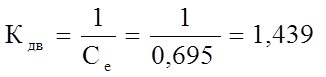
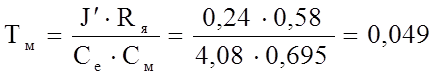
Тогда с учетом произведенных расчетов передаточная функция ДПТ равна:

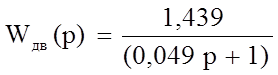                                                                    (8)

Р е д у к т о р (Р). Выбираем редуктор Пз-31,5 [3]. Его характеристики:

- Крутящийся момент М_кр, Н×м                                        125 ¸ 1500

- Радиус водила R, мм                                                               31,5

- Передаточные числа i                                                      6,3 ¸12,5

- КПД                                                                                            0,96

- n_max , мин^-1                                                                                3000

- n_min , мин^-1                                                                                  500

Так как передаточные числа для данного редуктора даны, то возьмем среднее значение

Согласно Топчееву, передаточная функция редуктора равна:

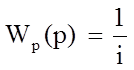                                                                                      (9)

подставим передаточное число и получим:

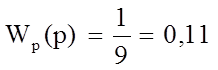                                                                          (10)

Р

К л а п а н  (Кл). в качестве исполнительного механизма был выбран быстродействующий электроклапан типа ЭКД-2347-73-А-ВО [3]. Его статистическая характеристика изображена на рисунке 3.

			где Р – давление, Х - перемещение

 

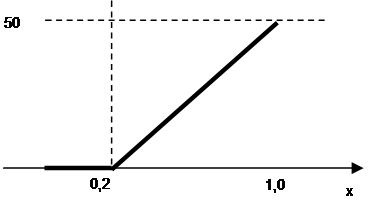Рисунок 3. Статистическая характеристика клапана.

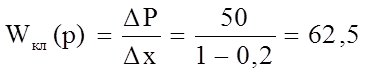                                                       (11)

Х и м и ч е с к и й  р е а к т о р  (ХР). Объектом регулирования является рабочий объем химического реактора, в котором поддерживаются заданные параметры. Согласно Топчееву резервуар с жидкостью имеет передаточную функцию [4]:

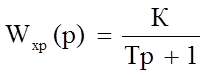                                                                           (12)

где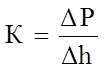

 = 0,36 - изменение давления при изменении уровня на 10 мм;

 = 10 мм – минимальная высота заливки.

Тогда

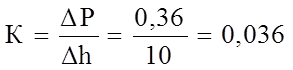
Так как передаточная функция химического реактора является инерционным звеном 1-ого порядка, то время связано с постоянной времени следующим соотношением:

                                                                                  (13)

Примем, что отсюда следует, что постоянная времени равна:

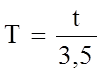
Время заполнения всего резервуара равно 6 мин, тогда:

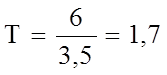
Исходя из полученных результатов, составим передаточную функцию химического реактора:

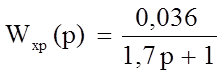                                                                         (14)

Д а т ч и к  д а в л е н и я  (ДТ). В качестве датчика выберем датчик давления, так как она измеряет давление и преобразовывает полученное значение в электрический сигнал, который обрабатывает микропроцессор. Так как среда в химическом реакторе агрессивна, поэтому наша датчик должен быть выбран с учетом тяжелых условий эксплуатации. На основе этого выбираем датчик давления, выпускаемую промышленностью для работы в особо тяжелых условиях, типа МВЭС-А [3].

Передаточная функция термопары:

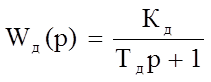                                                                           (15)

где К_д – коэффициент передачи (0,8);

       Т_д – постоянная времени датчика (0,005 с).

Тогда получим:

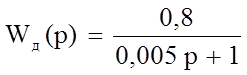                                                                      (16)

3.  Расчет передаточной функции всей системы и проверка системы на устойчивость

3.1.  Расчет передаточной функции системы

Для проверки системы на устойчивость необходимо исследовать ее разомкнутую систему и уже по ней судить о состоянии замкнутой системы. Основной сложностью является наличие нелинейных элементов в системе, в данном случае МП. Самым простым способом вычисления таких систем является Z – преобразование. Оно позволяет преобразовывать линейные элементы в дискретные и дальше работать с системой, как с линейной.

Тогда структурная схема разрабатываемой системы в виде передаточных функций представлена на рисунке 3.

 

Рисунок 4. – Структурная схема системы в виде передаточных функций

Передаточная функция разомкнутой системы будет иметь вид:

             (17)

то есть для нашей системы:

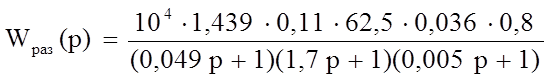
преобразуем

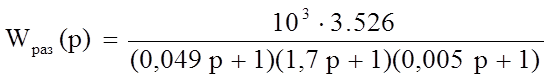                               (18)

Произведем Z – преобразования для каждого элемента системы. Частоту дискретизации выбираем равной частоте МП, то есть равной 5×10⁶ Гц.

3.2.  Z – преобразование системы

Микропроцессор по принципу действия является машиной дискретного действия, который выдает результаты расчета через установившийся период повторения. В промежутках между выдачей команд, выход МП сохраняет свое значение постоянным. В исследуемой системе на вход неизменяемой части системы подается единичная ступенчатая функция на протяжении всего периода повторения. Тогда непрерывная часть системы является, на входе которой действует подобная функция, является фильтром с фиксацией или фильтром с запоминанием.

Тогда отыскание передаточной функции разомкнутой системы с МП, представляет собой произведение (z-1)/z на Z – преобразование передаточной функции формулы (8). Формулы для данного преобразования берем в Топчееве.

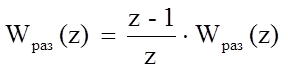                                                                 (19)