Проектирование эвольвентной цилиндрической зубчатой передачи и планетарного редуктора, страница 2

          Из этой области выберем смещение  равное 0.5, что согласовывается

с ГОСТ 16532-70

3.1.3. Построение станочного зацепления

Профиль зуба изготовляемого колеса (шестерни) воспроизводиться (образуется) как огибающая ряда положений исходного производящего контура реечного инструмента в станочном зацеплении. Такое образование профиля отражает истинный процесс изготовления колеса на станке. При этом эвольвентная часть профиля зуба образуется прямолинейной частью реечного производящего исходного контура, а переходная кривая профиля зуба с закругленным участком.

3.1.4. Построение зубчатого зацепления

По вычислениям с использованием ПЭВМ параметрам проектируемая зубчатая передача строиться в соответствии с рекомендациями методических указаний

3.2. Проектирование планетарного редуктора

          Цель проектирования - произвести оптимальный кинематический синтез планетарной передачи минимальных габаритов, удовлетворяющей дополнительным условиям

          Основные требования синтеза - выбор параметров планетарного редуктора минимальных габаритов, при котором обеспечиваеться заданное передаточное отношение с требуемой точностью

3.2.1. Исходные данные

1. Число сателлитов в редукторе к=3,

2. Модуль зубчатых колес m=2,0;

3. Передаточное отношение редуктора      

Задан планетарный механизм со смешанным зацеплением (с одним внешним и одним внутренним зацеплением).

Входное звено – первое звено;

Выходное – водило.

Подбор чисел зубьев.

Если бы ось в планетарном механизме стала неподвижной, то мы могли бы записать: 

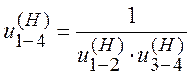                                         (1)

Обратим мысленно планетарный механизм в механизм с неподвижным водилом, для того чтобы использовать формулы для механизма с неподвижными осями зубчатых колес (применим метод обращения движения).

В обращенном движении каждое из звеньев будет иметь:

                  1 звено:   ω^*₁ = ω₁ + (–ω_н)

                  2 звено:   ω^*₂ = ω^*₃ = ω₂ + (–ω_н)

                  3 звено:   ω^*₃ = ω^*₂ = ω₃ + (–ω_н)

                  4 звено:   ω^*₄ = ω₄ + (–ω_н) = –ω_н

                  5 звено:   ω^*_н = ω_н + (–ω_н) = 0 , тогда из уравнения (1) получим

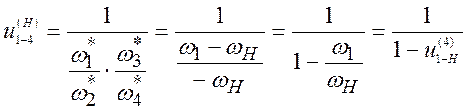
если (1) переписать через количество зубьев, то

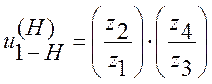, тогда уравнение передаточного отношения будет

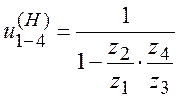 - плюсовой механизм               (2)

Подставим в уравнение (2) значения передаточного числа для заданного механизма:

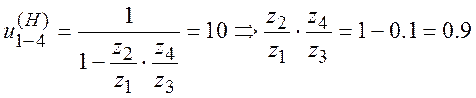
Разложим полученное число на взаимно простые сомножители А, B, C и D, которым числа зубьев должны быть соответственно пропорциональны. Так как колесо 3 не может быть больше колеса 4, то C не может быть больше D. Так как колесо 2 не может быть больше колеса 1, то A не может быть больше B. Пусть A =  10; В = 4; С = 4; D = 9.

Из условия соосности, которым определяется соосное расположение центральных колес планетарного механизма с водилом h, следует равенство межосевых расстояний зацепляющих колес:

;

так как для всех колес модуль одинаковый (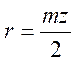), то уравнение соосности будет:  ;

Тогда формулы для подсчета зубьев будут:

;

;

;

;

Общий множитель q подбирается так, чтобы числа зубьев были целыми и  отсутствовал подрез у зубьев, т.е. ;; z₃ ³ 20 и z₄ ³ 85, и должно обеспечиваться отсутствие заклинивания в зацеплении сателлит – коронная шестерня, т.е.  и . Тогда учитывая данные требования, выберем q = 3, при котором число зубьев будет:

;

;

;

;

Проверим выполнение условий соседства и сборки:

1. Уравнение условия соседства имеет вид:

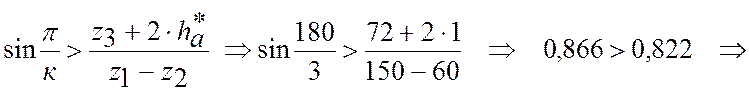
условие соседства выполнено.

2.  Уравнение условия сборки имеет вид:

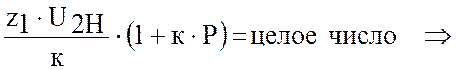
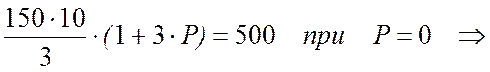
условие сборки выполнено.

Проверка передаточного отношения планетарного зубчатого механизма графическим способом.

I.  Вычислим значение радиусов делительных окружностей:

;

;

;

;

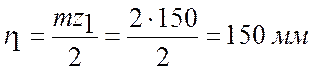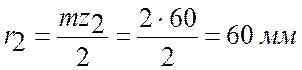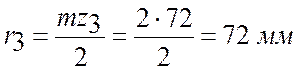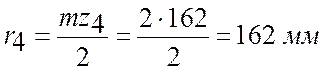Вычертим механизм по полученным значениям в масштабе:

μ_l  = 800 мм/м;

Выберем на выходном звене (на водиле) точку F так, чтобы O₁A=O₂F (O₁ и O₂ соосны).Зададимся произвольным отрезком АA`, которая изобразит линейную скорость т.А колеса 1. Масштаб скорости будет μ<sub>v</sub> = 1000 мм/м, так как принимается w=1 рад/с )Так как колесо 1 вращается вокруг O<sub>1</sub>, то скорость первого колеса будет O<sub>2</sub>A`. Точки

A, В и C лежат на оси симметрии колеса. В точке А колесо имеет такую же скорость. Колесо 2 и 3 изготовлены как единое целое. В точке С колесо 2 и 3 (блок сателлита) имеют мгновенный центр скоростей абсолютного движения, следовательно закон распределения линейных скоростей по звеньям 2 и 3 изображается отрезком СА` . В точке В линейная скорость блока сателлитов имеет скорость, изображенную отрезком ВВ`. В точке В водило h имеет такую же линейную скорость, но водило вращается вокруг оси O₂ , следовательно закон распределения линейных скоростей изображается линией O₂В`. Точка F водила имеет линейную скорость FF` , так как углы ψ_h и ψ₁ отложены в одну сторону, то и звенья вращаются в одну сторону, тогда

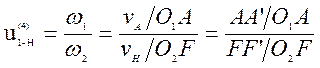
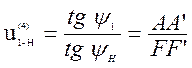
С чертежа отрезки АА` = 35 мм; FF` = 3,501 мм; тогда передаточное число будет:

Список использованной литературы:

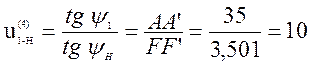
1.  С.А. Попов «Курсовое проектирование по ТММ»

2.  Тимофеев Г.А. «Силовой расчет механизмов»

3.  Лекции и семинары по ОПМ (4 семестр)

Использованные среды:

1.  AutoCAD 2002

2.  MathCAD 2000 PE

3.  Microsoft Word XP

4.  Пакет CorelDraw 11