![]()
|


![]()
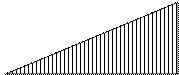
![]() 5,74м C
8,26м 0,18 критичною.
5,74м C
8,26м 0,18 критичною.
|
|
використавши нерівності:
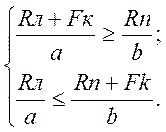
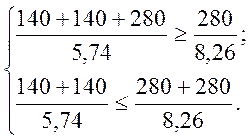
E
|
Умова виконується, критичною буде сила F2, яка знаходиться
![]() над вершиною трикутника. Підраховуємо максимальне
над вершиною трикутника. Підраховуємо максимальне
![]() значення реакції:
значення реакції:
, де: Rп – значення від постійного навантаження,
![]()
|
навантаження.
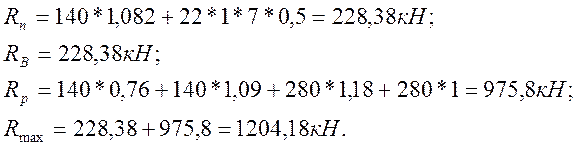 D
- за допомогою лінії впливу
D
- за допомогою лінії впливу
- згідно аналітичних розрахунків у 1-ій частині
Мінімальне значення опорної реакції R знаходимо, поставивши рухоме навантаження над
від’ємною частиною лінії впливу (дивися лист 18).
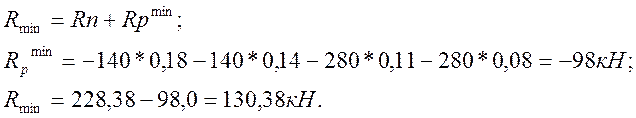 |
|||
 |
|||
|
|
|
![]()
|
|
|
|
|
|
|
|
|
|
. Аналогічно знаходимо екстремальні значення для згинального момента та поперечної сили в
перерізі 1.
Згинальний момент. Критичною – приймаємо останню (праву) силу рухомого навантаження, перевіримо нерівності:
F1 F1 F2 F2
л. в. М1
![]()
![]()

![]()
![]()
![]()
![]() 0,319
0,319
0,485 0,59 0,756
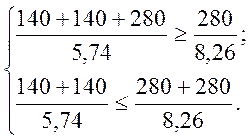 |
Нерівності задовольняються. Відшукуємо значення мінімального згинального момента.
Максимальний дорівнює нулю (відсутні додатні значення лінії впливу згинальних моментів).
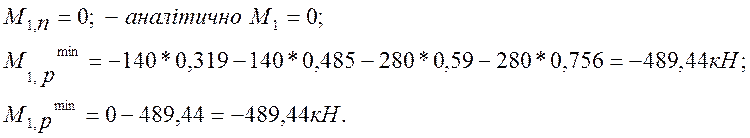 |
Поперечна сила. Знаходимо мінімальне значення поперечної сили (максимальне
дорівнює нулю). Невигідне положення рухомого навантаження видно з малюнку лінії впливу поперечної сили.
F1 F1 F2 F2
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
л. в Q1
![]()

![]()
![]()
![]()
![]()
![]() 0,553
0,553
0,773
0,912 1 1
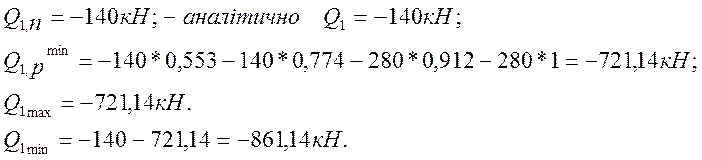 |
 |
|
|
|
![]()
|
|
|
|
|
|
|
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.