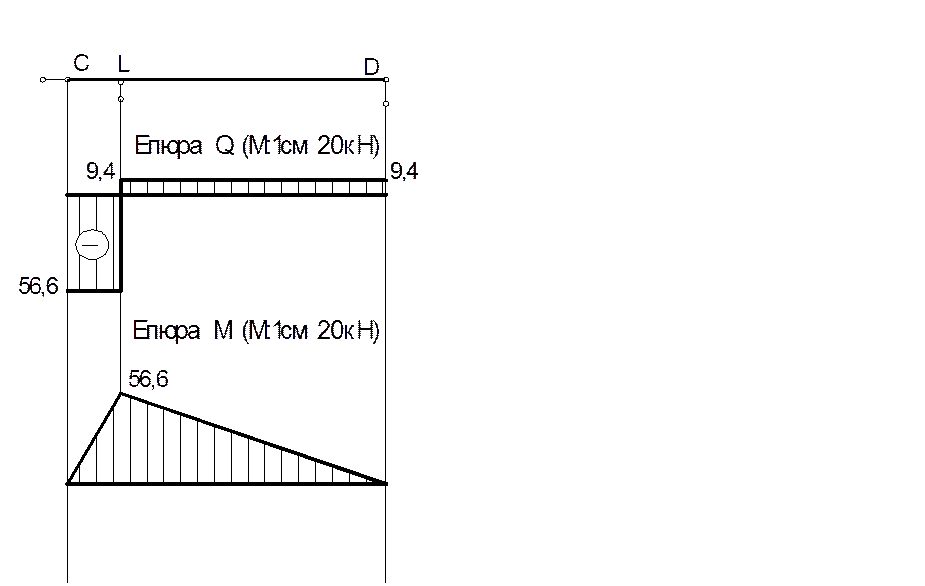
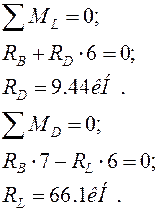 Ділянка CD: Розрахункова схема. Визначаємо
опорні реакції:
Ділянка CD: Розрахункова схема. Визначаємо
опорні реакції:
Побудова епюри поперечних сил.
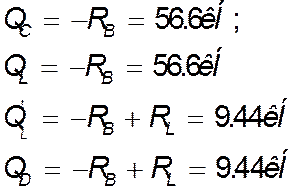 |
Побудова епюри згинальних моментів.
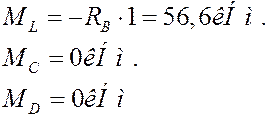 |
Ділянка DE: Розрахункова схема. Визначаємо опорні реакції:
Побудова епюри поперечних сил.
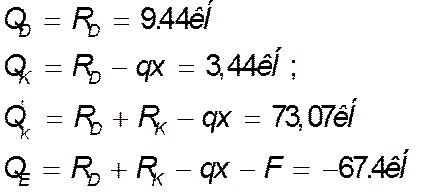 |
Побудова епюри згинальних моментів.
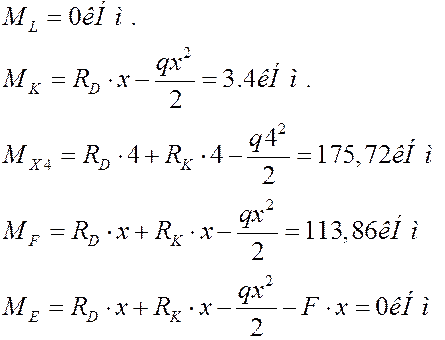 |
Обчислимо максимальний згинальний момент, підставивши в рівняння згинальних моментів ділянки BG координату, в якій поперечна сила дорівнює нулю, тобто х =4м.
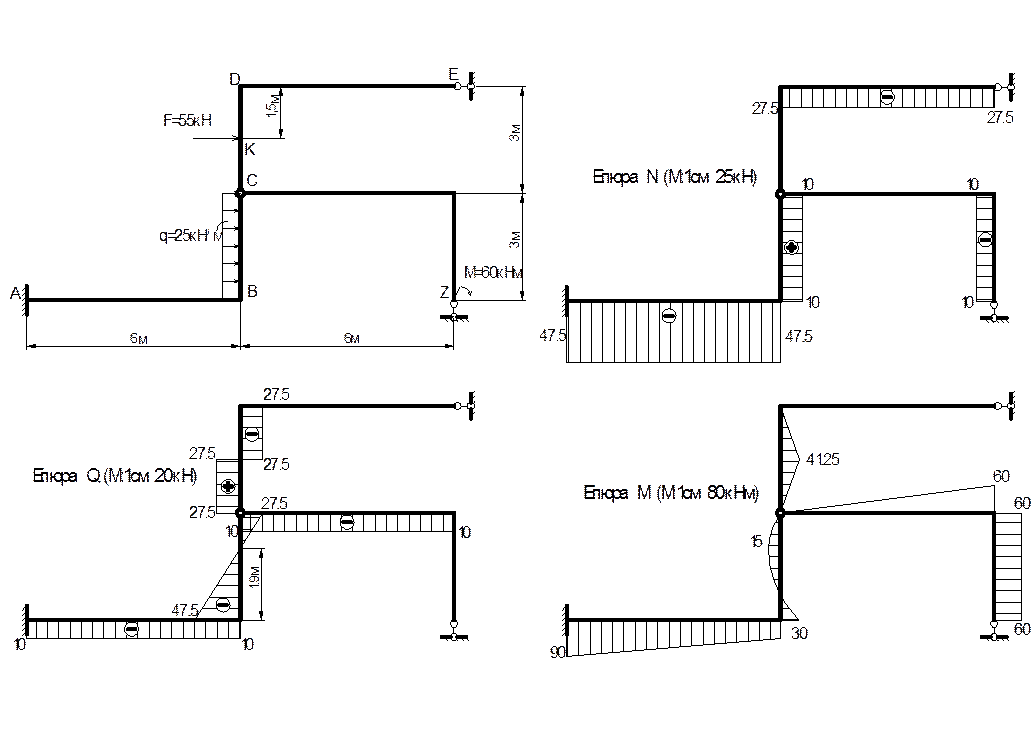 Розрахункова схема.
Розрахункова схема.
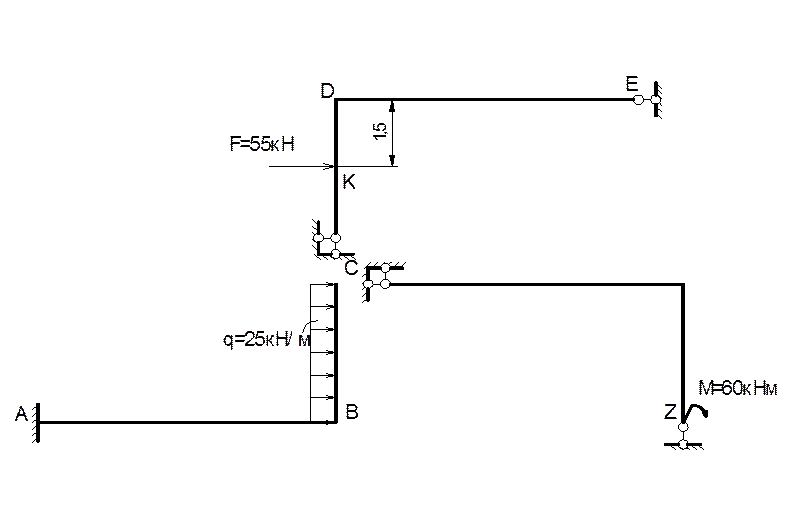 Поверхова
схема.
Поверхова
схема.
Визначаємо ступінь свободи системи
W= 3Д – 2Ш – Во = 3*3 – 2*2 – 5 = 0
Система є геометрично незмінною, бо перший диск жорстко затиснутий, а другий та третій - приєдну ються до нього за допомогою 3-х опорних стержнів кожний. Тому система статично визначна.
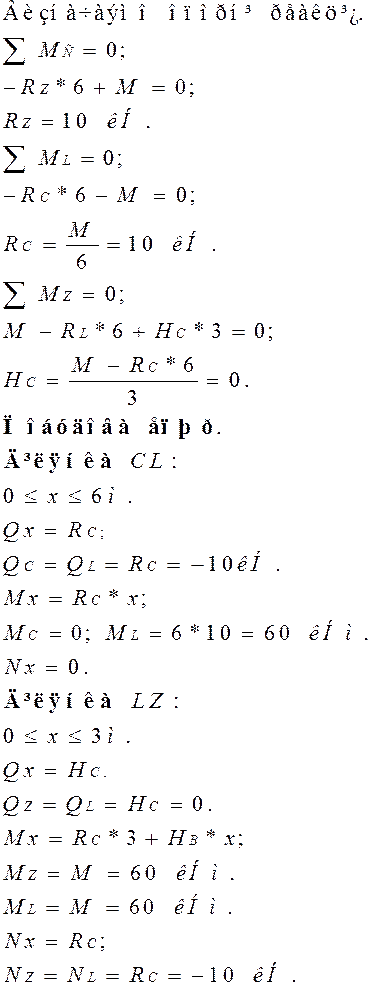 |
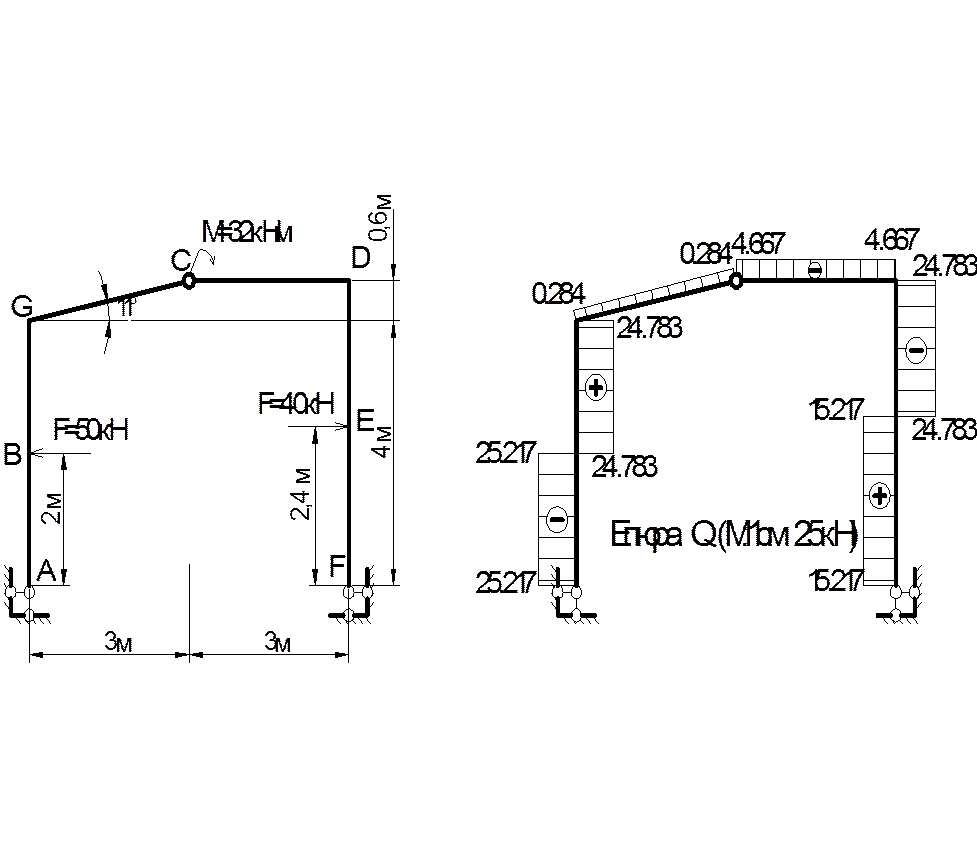
 Розрахункова схема.
Розрахункова схема.
W = 3 * 2 – 2 * 1 – 4 = 0.
Рама складається із трьох дисків (АС, СF, третій диск – нерухома основа), які з’єднані трьома
шарнірами (А, С, F) не розташованими на одній прямій. Тому рама геометрично незмінна та статично визначна.
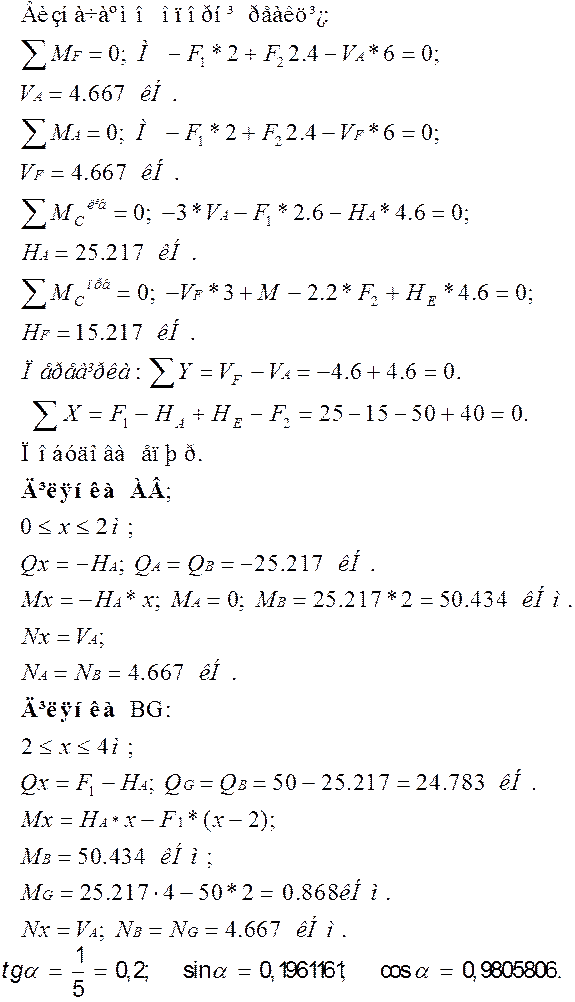 |
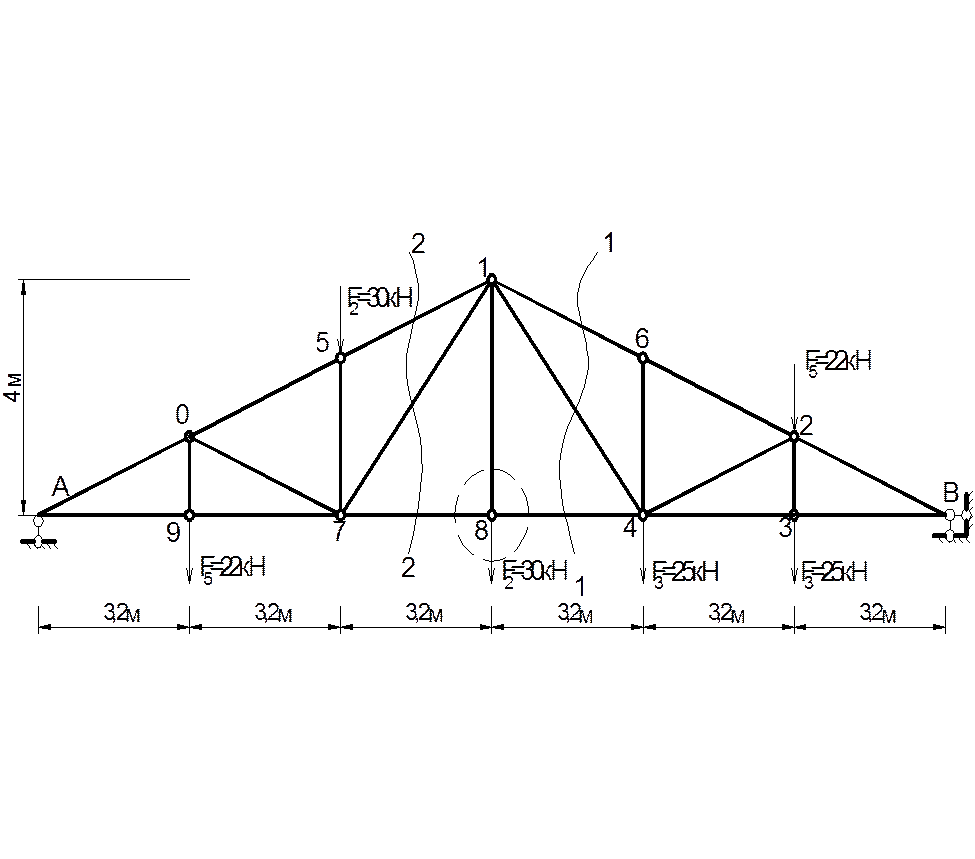 1.4. Визначення зусиль в стержнях заданого
вузла ферми
1.4. Визначення зусиль в стержнях заданого
вузла фермиРозрахункова схема ферми:
Статична перевірка вузла ферми
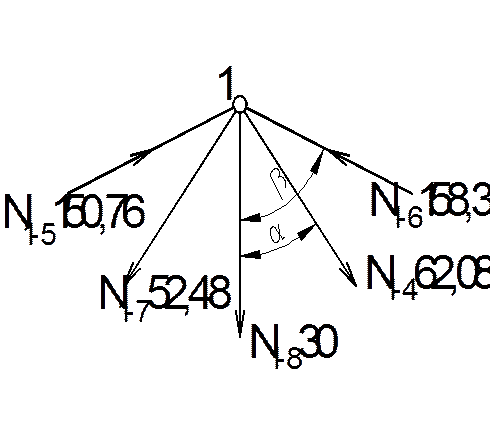
W = 2В – C – Вo = 2*12 – 21 – 3 = 0.
Так, як структура ферми гратчаста трикутної форми то ферма геометрично незмінна, а так як W=0, то вона статично визначна.
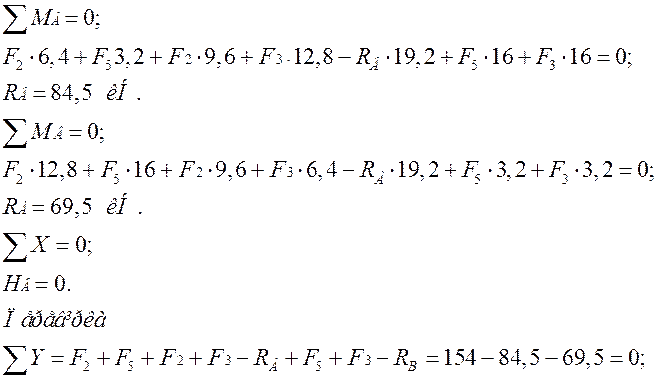 |
Визначаємо зусилля в стержнях вузла 8. Для цього використаємо спосіб вирізання
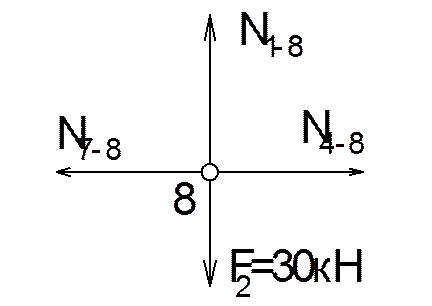
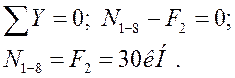 |
Визначаємо зусилля в стержнях вузла 1. Для цього використаємо спосіб перерізів
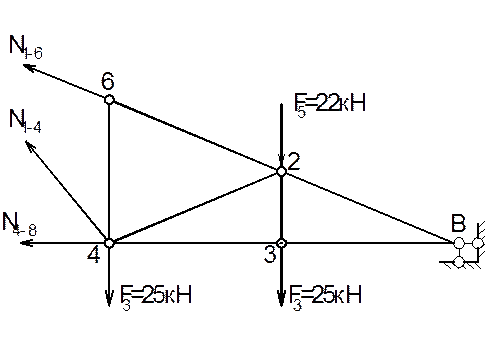 (перерізи 1-1, 2–2,
вказані на розрахунковій схемі ферми).
(перерізи 1-1, 2–2,
вказані на розрахунковій схемі ферми).
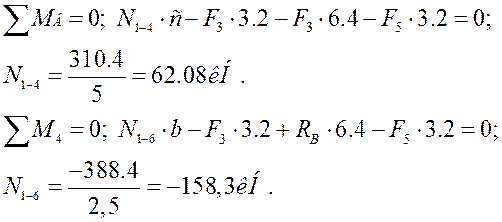 |
Для визначення відстані c і b розглядаємо трикутнички, які подані нижче
![]() За теоремою Піфагора знайдемо
гіпотенузи таких трикутників 481 та В81. Відповідно довжина стержня
1-4 та відстань від 1 до В
За теоремою Піфагора знайдемо
гіпотенузи таких трикутників 481 та В81. Відповідно довжина стержня
1-4 та відстань від 1 до В
Розглянемо трикутники 481 та ВК4 вони подібні (за рівними трьома кутами), з подібності трикутників слідує що 1-4 відноситься до 4-В, як 1-8 до ВК, тому
 Розглянемо трикутник 1Е4 та 4ЕВ знайдемо спочатку відстань ЕВ
а потім за теоремою Піфагора b
Розглянемо трикутник 1Е4 та 4ЕВ знайдемо спочатку відстань ЕВ
а потім за теоремою Піфагора b
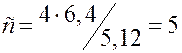 |
|||
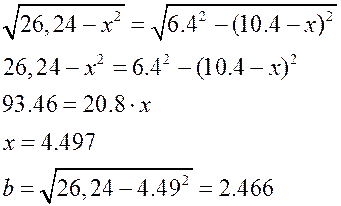 |
|||
Розрізаємо ферму перерізом 2, і
розглядаємо праву відсічену частину. 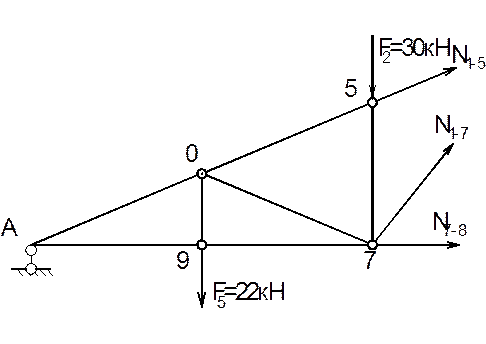
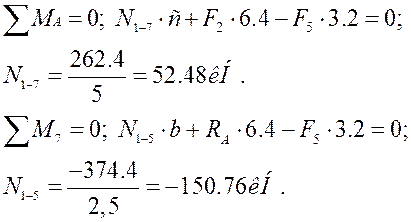
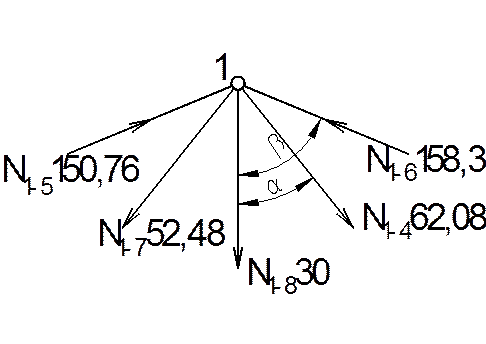 Зробимо
перевірку вузла 1 на рівновагу, щоб впевнитися, що наші обрахунки вірні
Зробимо
перевірку вузла 1 на рівновагу, щоб впевнитися, що наші обрахунки вірні
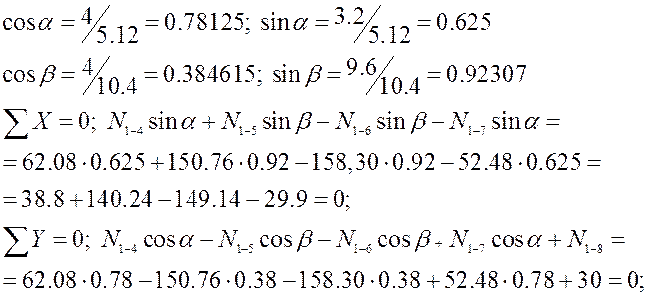 |
частина друга
Побудова ліній впливу зусиль в балці,
рамах та фермі з визначенням
в балці зусиль від постійного
та тимчасового навантаження
Схема одиничного завантаження
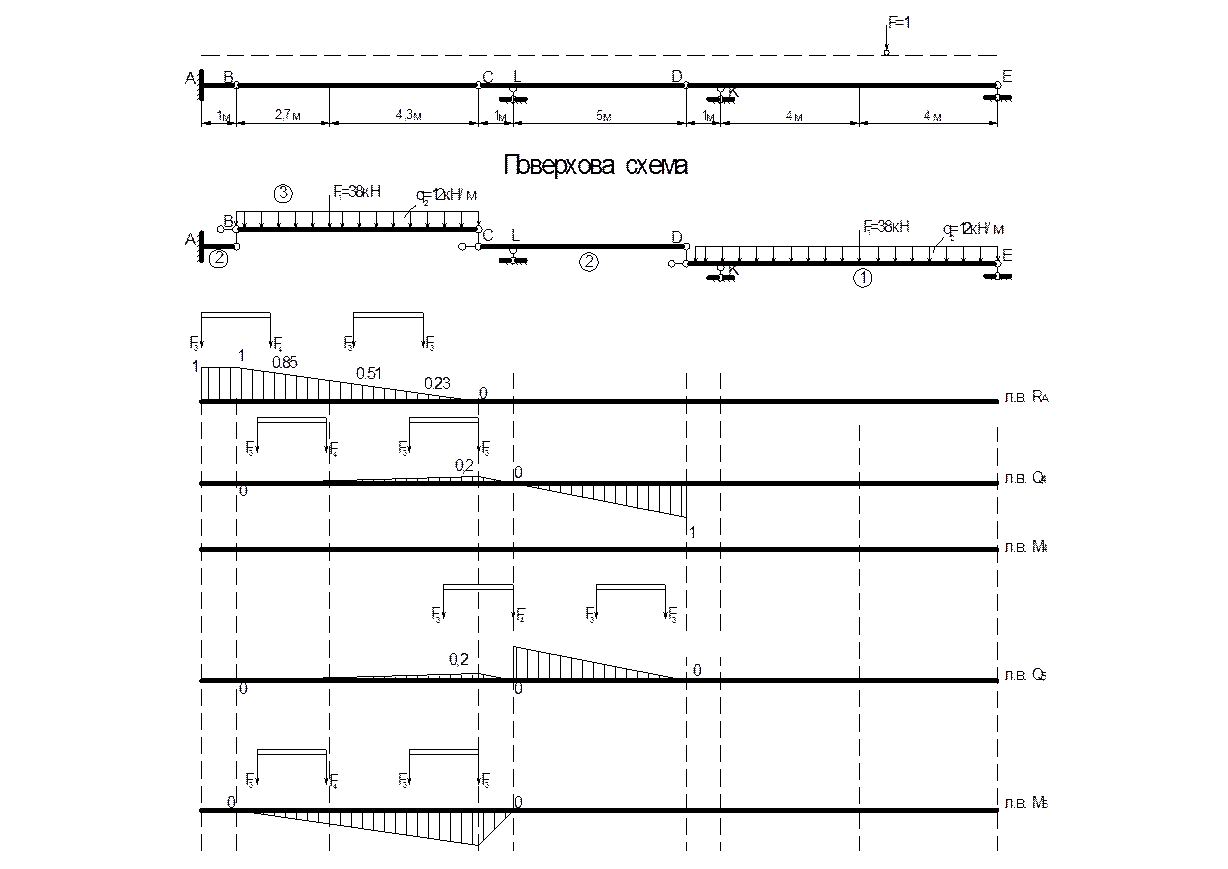
і рухомого навантаження.
![]()
![]()
![]()
![]() 2м 2,4 м 2м
2м 2,4 м 2м
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() F3 = 50кН ;
F3 = 50кН ;
![]()
![]()
|
|
|
|
Для поперечна сила Q4: Нехай рухоме навантаження знаходиться в заданому положенні, відкладаємо вектори усіх сил в масштабі по лінії АD, проводимо лінію від кінця додатної частини лінії впливу трикутної форми (т. В) до кінця векторів всіх сил (т. D). Потім проводимо з точки С (яка знаходиться під вершиною трикутника) лінію СЕ паралельну лінії BD. Точка Е потрапила на сили F3, отже припустимо, що вона і є критичною. Перевіримо умови нерівностей, згідно яких. Перевіримо правильність знаходження
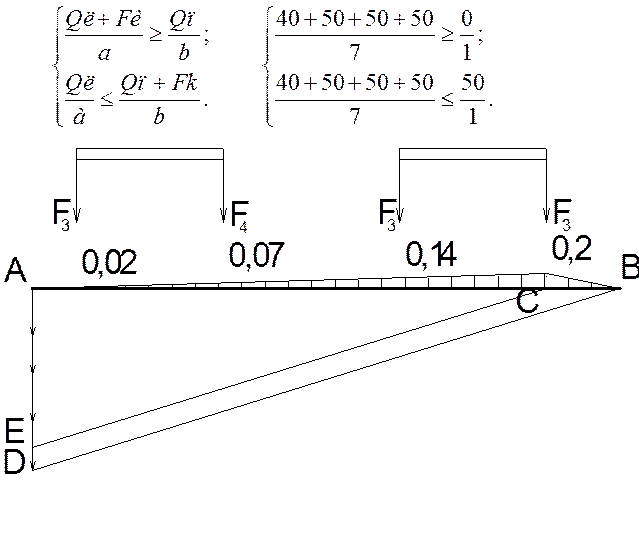 |
![]() Умова виконується, критичною буде
сила F2, яка знаходиться над вершиною трикутника. Підраховуємо
максимальне значення реакції.
Умова виконується, критичною буде
сила F2, яка знаходиться над вершиною трикутника. Підраховуємо
максимальне значення реакції.
![]() де: Qп- постійне навантаження,
де: Qп- постійне навантаження,
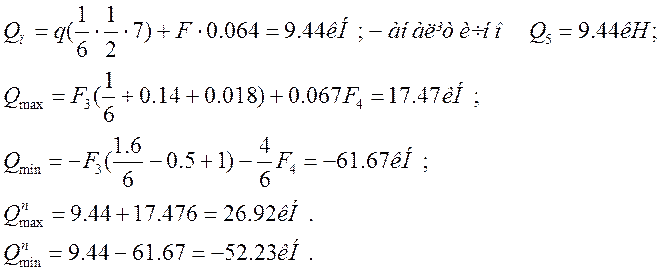 - максимальне рухоме
навантаження
- максимальне рухоме
навантаження
Максимальний дорівнює нулю (лінія впливу рівна нулю), аналітично згинальний момент теж рівний нулю.
Максимальне значення реакції R буде дорівнювати:
- за допомогою лінії впливу
- згідно аналітичних розрахунків у 1-ій частині
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.