Оптимальное уравнение для данной системы принимает вид:
U(t)= -D-1BTG(t)m(t) (13),
а среднее значение функционала (2)
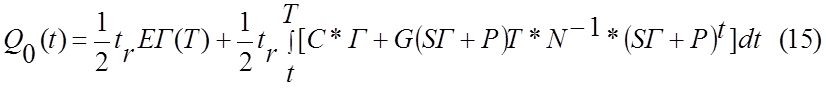Q(t)=Q0(t)+1/2mTG(t)m (14)
где –
- m – математическое ожидание процесса w(x,t);
- Г – матрица вторых моментов этого процесса;
- N=Ф*ФТ;
- G – матрица, определяемая из уравнения (5).
В случаях “б” и “в” моменты “m” и “Г” могут быть найдены из уравнений:
m’ =(f+Am+SГ+P)T*N-1(Z-G-Sm) (16);
Г’ =A Г+ ГAT+F*FT-(S Г+P)TN-1(S Г+P) (17);
Г(t0)=Г0; m(t0)=m0;
Апостериорное среднее m(t) является решением последних уравнений и представляет собой оптимальную оценку для процесса x(t) (оценка Каимана-Бьюси). Такие оценки получаются в системе измерения, описываемой уравнениями:
x’=f(t)+A(t)x+f(t)dw(t)/dt (18)
z(t)=g(t)+S(t)x(t)+Ф(t)dw/dt (19).
Из рассмотренного выше можно сделать следующие выводы:
1. Сопоставление выражений для оптимального управления (13),(8),(4) показывает, что для формирования управления во всех трех рассмотренных случаях используются апостериорные средние оценки вектора состояния на выходе канала ТС. Алгоритм управления идентичен во всех трех случаях, причем, что примечательно, в самом оптимальном регуляторе не используется матрица вторых моментов оценки вектора состояния. В силу этого такой регулятор может быть назван детерминированным. Таким образом, если представить детерминированную систему управления бу шумов, значение вектора состояния которой совпадает с вектором апостериорных математических ожиданий стохастической системы, то оптимальные регуляторы и сами управления U(t) в обеих системах будут полностью совпадать.
2. Линейная стохастическая система управления с показателями качества (2) или (6) состоит из двух относительно не зависимых систем: оптимального регулятора, о котором шла речь в пункте 1, и системы оценки первых и вторых моментов вектора состояния, описываемой уравнениями (16), (17), (18), (19).
Такая система измерения называется оптимальным линейным фильтром. Возможность разделения линейной оптимальной системы управления на детерминированный оптимальный регулятор и оптимальный линейный фильтр является основным содержанием теоремы разделения. Все отличие трех рассмотренных групп каналов ТС состоит в параметрах оптимального линейного фильтра и в матрицах вторых моментов “Г”.
3. Составление показателей качества функционирования системы управления (4а), (9), (14) показывает, что для всех трех групп каналов ТС при равенстве апостериорных математических ожиданий отличия содержатся в значениях Q(t), которые в свою очередь монотонно зависят от величины следа матрицы вторых моментов tr Г(t). Учитывая ,что для вычисления следа необходимо предварительно произвести диагонализацию матрицы “Г”, а диагональные элементы имеют смысл дисперсии вектора состояния, можно сделать вывод о том, что качество управления в значительной мере определяется величиной этой дисперсии, т.е. чем больше дисперсия, тем больше значения функционала и тем хуже качество.
Основными факторами, определяющими минимальную величину дисперсии, являются как это следует из уравнения (17), параметры системы измерения и статистические свойства процесса w(t). Учитывая, что систему измерения мы должны разделить на две последовательно-соединенные части – собственно измеритель и канал ТС, удобно от величины trГ перейти к энтропии оценок вектора состояния системы , которая определяется из соотношения:
Низм=1/2trlnГ (20).
Переход к энтропии позволяет аддитивно разделить ее на энтропию собственно линейного фильтра и энтропию канала ТС, причем:
Низм=Нлф+НТС (21).
Как уже отмечалось, матрица вторых моментов, а следовательно, и энтропия линейного фильтра при фиксированных входных воздействиях на систему управления определяется параметрами линейного фильтра.
В свою очередь энтропия канала ТС зависит от шумов в этом канале и параметров системы модуляции и кодирования. В связи с этим возникает вопрос, можно ли осуществлять оптимизацию параметров линейного фильтра и систем модуляции и кодирования не зависимо друг от друга. Учитывая замкнутость системы управления, это в общем случае делать нельзя, т.к. выбор того или иного способа кодирования изменяет дисперсию процесса «Х», что в свою очередь влияет на выбор оптимальных параметров устройства оценки процесса «Х». Однако, в случае, когда рассматривается линейная система, причем все операторы, а также матрица «Е», входящая в выражение для функционала качества являются диагональными, оказывается, что оптимизацию параметров линейного фильтра и параметров системы кодирования и декодирования можно осуществлять независимо.
Очевидно, наличие нелинейной системы кодирования декодирования не позволяет говорить о том, что наша задача является линейной. Здесь мы рассматриваем упрощенный вариант задачи, когда предполагается, что выбор показателя качества и пространства состояний «Х» осуществлен так, чтобы се нелинейные операторы физической системы были представлены как линейные операторы ее математической модели.
С учетом всего вышеизложенного можно сделать вывод о том, что для оптимизации замкнутой системы управления за счет выбора системы кодирования и модуляции достаточно минимизировать только энтропию канала ТС, т.е. min НТС. Наконец учитывая, что в одномерном случае НТС=1/2lns2 (22), где s2 дисперсия шумов в канале ТС, может ставиться задача по минимизации шумов передачи в каналах ТС. Если представить , что s2 в свою очередь является суммой шумов квантования и шумов, возникающих из-за искажения сигналов в канале связи, т.е. s2=Pz=Ркв+Ркан (23),то можно утверждать, что минимизация выражения «РS» за счет выбора систем кодирования и модуляции будет достаточной для минимизации показателей качества (4), (8), (13). И, таким образом , выражение (23) может быть выбрано как критерий сравнимости различных способов передачи каналов ТС.
БИТТУ
Факультет: Инженерно - строительный.
Кафедра: УИТ.
Отчет по практике .
Утверждено Выполнил:ст. гр. УИТ-51 зав.кафедрой УИТ Жалилина Ю.А.
Академик МАН ВШ, профессор Руководитель дипломного Власов В.В. проекта
«______» ___________ 2001 Хречков Н.Г.
«______» ______________ 2001г
Балаково 2001
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.