Классификация исходов
Выше рассматривалась дуополия на рынке, где обе фирмы уже несли затраты, связанные с открытием производства. И где во всех точках, для которых имеется как возможность входа, так и его отсутствие, укоренившаяся фирма будет производить выпуск, равный ее мощности до входа. Исходя из этого, прибыли обеих фирм можно записать как функции от их выпусков, т.е.
pi (x1 , x2 ) = Ri (x1 , x2 ) – fi – (wi+ ri) xi
Для удобства будем обозначать точку (x1 , x2 ), соответствующей ей буквой на графике, p1 всегда будет положительной, прибыль фирмы 2 монотонно убывает вдоль кривой ее функции реакции от T к V, а в зависимости от знака p2 возможны следующие случаи:
Случай 1. p2 (T) < 0 .Тогда потенциальный новичок не получает прибыли ни при каком из видов равновесия и поэтому он вообще не войдет в отрасль. Фирма 1 же останется чистым монополистом с выпуском M1.
Случай 2. p2 (V) > 0. Потенциальный новичок получает положительную прибыль в любом случае и укоренившаяся фирма не может предотвратить его вход, но зато, если будет вычислять свою прибыль вдоль отрезка TV, она в состоянии выбрать наилучшую позицию в дуополии.
Случай 3. p2 (T) > 0 > p2 (V). Здесь имеется точка B = (B1,B2) на отрезке TV для которой p2(B) = 0. Если фирма 1 устанавливает свои производственные мощности выше B1, то потенциальный новичок будет считать сою прибыль отрицательной по Нэшу и не войдет в отрасль. Таким образом, точка B1 олицетворяет собой тот уровень мощность, который был бы достаточен для предотвращения входа фирмы 2. И если фирме 1 доступна эта информация, то она может узнать, выгодно ли ей предотвращать вход.
Подслучай 1. Если B1 < M1, то монопольный выпуск фирмы 1 является достаточным для предотвращения входа. Если B1 > M1, то укоренившейся фирме следует поддерживать свой выпуск и свою мощность на уровне более высоком, чем она бы захотела, будучи монополистом. Для предотвращения входа ей нужны мощности превосходящие B1. Укоренившаяся фирма захочет использовать все мощности для своего монопольного выпуска, и ее прибыль будет p1(B1, 0) = 0. Возможно также допущение входа с последующей возможностью занять наилучшую позицию в условиях дуополии, которая может быть либо точкой касания отрезка TV, либо угловым решением в V. Назовем эту позицию обобщенной точкой Штакельберга S с координатами (S1, S2). Тогда:
Подслучай 2. p1 (S) < p1(B1, 0), когда лучше предотвратить вход, выбрав ограничительные мощности или ограничительный выпуск B1, с соответствующей ценой.
Подслучай 3. p1 (S) > p1(B1, 0), когда лучше допустить вход.
ОБОБЩЕНИЯ И МОДИФИКАЦИИ
Первое обобщение – рассмотрение альтернативного равновесия после входа, когда новичок возлагает на себя роль количественного лидера. Тогда фирма 2 выбирает точку на кривой реакции укоренившейся фирмы с целью максимизации своей собственной прибыли. Однако фирма 1 оставляет за собой право определить, какую именно функцию реакции предоставить новичку.

Тогда на рисунке 4 мы можем продемонстрировать возможности влияния на решения новичка, которые получает укоренившаяся фирма.
Пусть F = (F1,F 2) – обычная точка Штакельберга, когда фирма 2 является лидером, фирма 1 – последователем, принимая во внимание затраты на расширение мощности, т.е. используя кривую MM`. Если фирма 1 устанавливает уровень мощности меньше, чем F1, то ее кривая реакции перейдет с NN` на MM`, слева от F. Тогда прибыль фирмы 2 будет достигать на этой кривой реакции максимума в точке касания F. Если между F1 и T1, то в вершине кривой реакции первой фирмы, лежащей на MM`, при равновесии, находящимся на отрезке FT. Справа от T – касательное решение на TV, т.е. p2-изолиния будет касаться вертикального отрезка кривой реакции фирмы 1.
Точка вертикального касания – наилучший выбор для фирмы 2 до тех пор, пока k1 ≤ Q1 . Для k1 > Q1 она уже предпочтет точку G.
Несмотря на то, что правила игры требуют от укоренившейся фирмы отказаться после входа от количественного лидерства, она может использовать свой начальный выбор производственных мощностей, чтобы отвоевать себе ограниченную инициативу. Тем самым наилучшим выбором для фирмы 1 является точка на отрезке TQ .
Второе обобщение затрагивает функцию затрат. Заменим вид (1) на функцию затрат, более непрерывно зависящую от уровня мощности:
C1 = C1( x1 ,k1 ) (2)
Эта функция выпукла и возрастает по x1. Для каждого x1 определено значение k1, минимизирующие затраты, поэтому C1 убывает по k1 до этого значения и возрастает после него. Более высокий уровень k1 снизит предельные затраты :
C1x1k1 < 0
В этом случае нижние индексы обозначают частные производные.
Итак, фирма 1 установила уровень своей мощности равным k1. Кривая реакции фирмы 2 остается прямой. Фирма 1 максимизирует R1( x1 , x2) - C1( x1 ,k1) по x1 для данных x2 и k1. Из вышесказанного можно вывести условие первого порядка R1x1 ( x1 , x2) - C1 x1 ( x1 ,k1) = 0 (4) и условие второго порядка R1x1 x1 ( x1 , x2) - C1 x1 x1 (x1 ,k1) < 0 (5).
Уравнение (4) определяет функцию реакции фирмы 1 после входа и описывает ее изменение при изменении k1. Если взять полный дифференциал, то можно вывести:
Из чего следует, что наклон функции реакции отрицателен, так как увеличение выпуска второй фирмы снижает предельную выручку первой.
Рассмотрим рис. 5, где пунктирными линиями показаны кривые реакции фирмы 1 в зависимости от выбора k1. Каждая точка пересечения такой кривой с кривой RR`, является точкой пересечения по Нэшу. Это означает, что фирма 1 остается практически полновластным хозяином в отрасли, так как с помощью выбора мощности может выбрать любую точку в некотором интервале на кривой реакции фирмы 2.
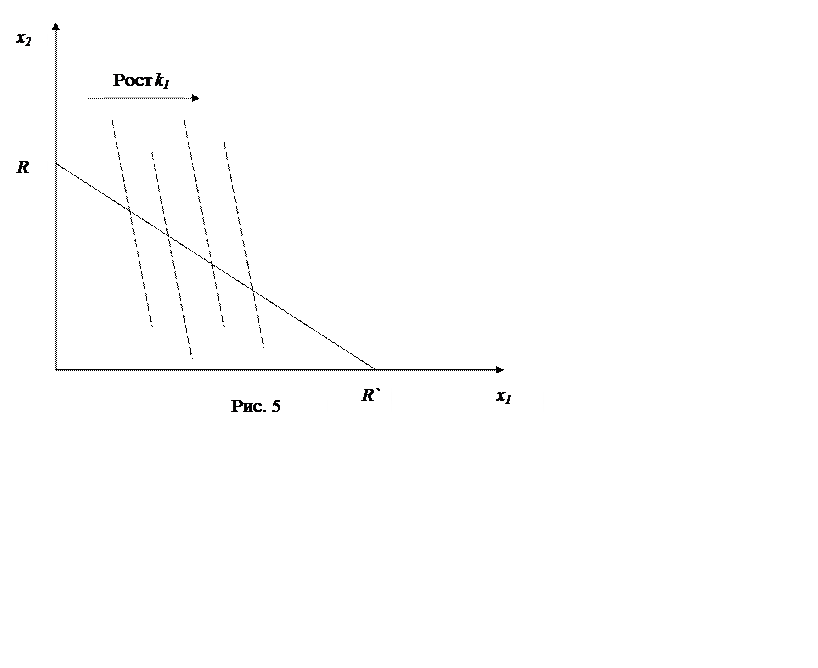
Однако в этом случае имеются затраты, которых не бывает при обычном количественном лидерстве. Чтобы увидеть это, рассмотрим более подробно равновесие. Фирма 2 максимизирует R2(x1 , x2) – C2(x2), поэтому ее функция реакции задается условием
(6).
Условия (4) и (6) определяют равновесие в дуополии как функцию от k1.
(7)
(8)
Где D - определитель матрицы коэффициентов. Фирма 1 использует его для выбора k1 с целью максимизации прибыли, следовательно:
(9)
В лучшей точке дуополии коэффициент при dk1 в (9) равен нулю, все три множителя в числителе первого члена отрицательны, D - положителен, тогда.
И мы видим, что фирма 1 доводит свои мощности до объема, превосходящего тот, который оптимизирует ее выпуск
Третье обобщение касается жесткой концепции мощности, но при ценовой дуополии.
Рассмотри рис. 6, где RR` - кривая реакции потенциального новичка. Кривая MM` соответствуют случаю, когда мощности расширяются у потенциального новичка, NN` - когда не расширяются. Первая кривая соответствует случаю, когда x1 ³ k1, вторая – когда x1 ≤ k1. Граничная кривая x1 = k1 показана для определенного значения k1. Жирной линией выделена соответствующая кривая реакции укоренившейся фирмы. И тогда место k1 укоренившаяся фирма может обеспечить себе в качестве равновесия по Нэшу любую точку отрезка TV, лежащего на кривой реакции потенциального новичка. Это свидетельствует о том, что преимущество первого выбора мощности дает возможность лидировать укоренившейся фирме в данной ситуации.

заключение
Итак, с помощью нескольких простых моделей мы обосновали утверждение о том, что роль не подлежащих пересмотру решений об инвестициях в предотвращении входа заключается в изменении в свою пользу укоренившейся фирмы начальных условий игры. Причем неважно, какие правила в этой игре установлены. Стоит, правда, заметить, что ни одной из этих моделей нельзя придать статус универсальной значимости, однако при отсутствии после входа у укоренившейся фирмы любых односторонних преимуществ решение по Нэшу выглядит весьма привлекательным.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.