




Министерство образования Российской Федерации
Уральский государственный технический университет – УПИ
филиал в г. Краснотурьинске
кафедра электротехники
по теме: «Цепь постоянного тока»
преподаватель: Хлызов М.В.
студент: Бурлов А.С.
Горбунова С.М.
Грязева Е.О.
Калинин К.
Сорокина С.С.
группа: Р-131КТ
2003
Цель работы: Проверить принцип наложения и свойство взаимности в цепях постоянного тока, состоящих из участков с постоянными сопротивлениями, в которых зависимость напряжения от тока выражается прямой линией (линейных цепях).
Программа работы:
1. Проверить принцип наложения.
2. Проверить свойство взаимности.
3. Определить собственные и взаимные контурные сопротивления.
4. Определить собственные и взаимные проводимости.
5. Проверить метод эквивалентного генератора.
Выполнение работы:
1.
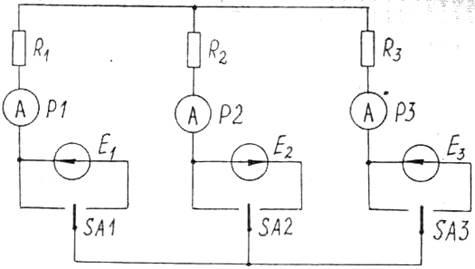 |
|
Токи ветвей |
Включены источники |
|||
|
Е1 |
Е2 |
Е3 |
Е1, Е2, Е3 |
|
|
I1, A |
0,46 |
0,22 |
-0,27 |
0,41 |
|
I2, A |
-0,19 |
-0,42 |
-0,2 |
-0,81 |
|
I3, A |
-0,27 |
0,2 |
0,47 |
0,4 |
|
Алгебраическая сумма токов в узле |
0 |
0 |
0 |
0 |
Вывод: по данным, полученным в ходе проведения работы, видно выполнение принципа наложения, который заключается в следующем: ток в любой ветви сложной цепи с несколькими ЭДС может быть представлен как алгебраическая сумма токов этой же ветви от действия каждой из ЭДС порознь. Сумма токов в узле, при действии каждой ЭДС отдельно и всех их вместе, как это видно из таблицы, равна нулю, что подтверждает первый закон Кирхгофа, следовательно, принцип наложения выполняется верно.
2. Проверка свойства взаимности (по таблице 1.1)
Для проверки свойства взаимности обратимся к таблице 1.1. Рассмотрим ветви 1 и 3. При включении первой ЭДС в третей ветви течёт ток равный –0,27 А, при включении третей ЭДС в первой ветви течёт ток равный также –0,27 А. Это говорит о том, что свойство взаимности полностью выполняется.
3. Определение собственных и взаимных контурных сопротивлений
|
Ветви |
Е, В |
UR, B |
I, A |
R, Ом |
|
1 |
7,8 |
4 |
0,42 |
9,5238 |
|
2 |
7,9 |
11,6 |
-0,8 |
14,5 |
|
3 |
8,2 |
4,3 |
0,41 |
10,4878 |
По измеренным сопротивлениям ветвей (таблица 1.2) найти собственные и взаимные контурные сопротивления, проверить контурные уравнения:
![]()
![]()
Выберем два контура: К1 и К2 (см схему выше). Найдём собственные и взаимные сопротивления этих контуров.
![]() Ом
Ом
![]() Ом
Ом
![]() Ом
Ом
Найдём контурные токи I1 и I2 по методу контурных токов.
Составим
три матрицы ![]() ,
, ![]() и
и
![]() :
:
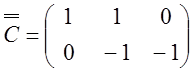 ,
, ![]() ,
, 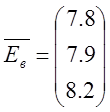
Воспользуемся следующими формулами:
![]() ,
, ![]() ,
,
![]()
Объединим их:
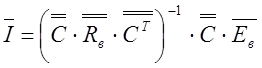
Подставим в данную формулу матрицы и посчитаем результат:
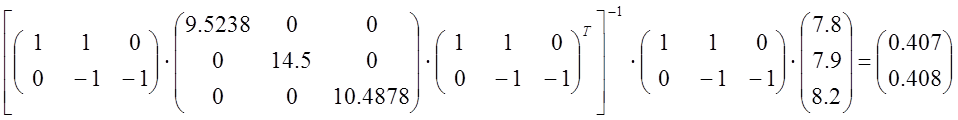
Ток в первом контуре будет равен I1=0.407 А, во втором – I2=0.408 А
ЭДС
первого контура будет равна ![]() В, второго –
В, второго – ![]() В
В
Найдем теперь ЭДС контуров по контурным уравнениям:
![]()
![]()
Сравнивая полученные значения ЭДС можно сделать вывод, что контурные уравнения выполняются.
4. Определение собственных и взаимных проводимостей
4.1. По данным, занесённым в таблицу 1.1, определить собственные и взаимные проводимости, входящие в уравнения, которые связывают контурные токи и контурные ЭДС, а именно:
![]()
![]()
Собственные проводимости определяются отношением тока к ЭДС в этом контуре при равных нулю ЭДС в остальных контурах.
Взаимная проводимость определяется отношением тока в данном контуре к ЭДС в другом при равных нулю ЭДС в остальных контурах.
Из выше следующих формул выразим матрицу G:
![]()
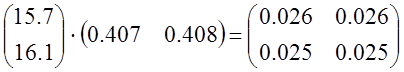
G11=0.026 G12=0.026
G21=0.025 G22=0.025
4.2. По найденным контурным сопротивлениям (пункт 3) вычислить собственные и взаимные проводимости и сравнить их с ранее определенными проводимостями в пункте 4.1.
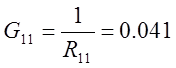
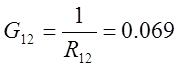
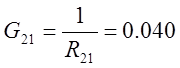
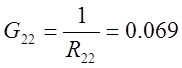
Различие между проводимостями можно объяснить тем, что метод снятия показаний несовершенен (все показания снимались «на глаз», так как приборы были аналоговыми), а также можно сослаться на погрешность приборов.
5. Проверка метода эквивалентного генератора
Из первого контура:
E1+E2=Uxx+U2, откуда Uxx= E1+E2–U2= E1+E2–R2·I2
Из второго контура:
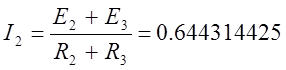 А
А
Uxx=7.8+7.9–14.5·0.644314425=6.357440831 B
Найдем входящее сопротивление:
![]()
![]()
![]()
![]()
![]()
![]() R2
R2
R3
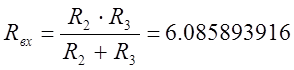 Ом
Ом
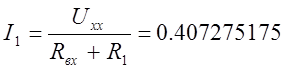 А
А
Ток, полученный в результате расчётов по методу эквивалентного генератора, и ток, измеренный в ходе лабораторной работы, практически совпадают, что говорит о том, что метод эквивалентного генератора пригоден для расчета токов без использования каких-либо специальных приборов.
Вывод (общий):
В результате проделанной лабораторной работы мы изучили цепь постоянного тока, а в частности, проверили принцип наложения, свойство взаимности, определили собственные и взаимные контурные сопротивления и проводимости, а также проверили метод эквивалентного генератора.
В первом пункте работы, при проверке принципа наложения, мы измеряли силу тока в ветвях при действии каждой ЭДС в отдельности и всех их вместе. Принцип наложения выполнился.
Второй пункт работы проводился теоретически, на основе данных снятых в первом пункте. Свойство взаимности, проверяемое в данной части работы, также выполнилось.
Далее, для определения собственных и взаимных контурных сопротивлений и проводимостей, мы с помощью вольтметра измерили силу тока в каждой ветви при действии всех ЭДС, напряжение на каждом сопротивлении и ЭДС создаваемое источниками тока.
В последнем пункте работы, для проверки метода эквивалентного генератора, мы, по своему желанию, выбрали резистор, по отношению к которому проверялся метод, всё рассчитали и сравнили полученные результаты с данными таблицы 1.2, которые практически совпали (погрешность ≈3%).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.