Отчет по учебной исследовательской работе «Исследование текстового документа», страница 4

Значение S - количество символов измеряется средствами Word: «Сервис», «Статистика», «Знаков (с пробелами)».

Значение Z - емкость файла, хранящего выбранную страницу, измеряется средствами Windows.

Значение u удельной емкости вычисляется по формуле (1):

u_i = Z_i / S_i,                                                                   (1)

где i – число страниц с текстовым документом, i = 1, 2, 3, …, 10.

Значение pu приведенной удельной емкости вычисляется по формуле (2):

pu_i = (Z_i – Z₀) / S_i,                                                      (2)

где i – число страниц с текстовым документом, i = 1, 2, 3, …, 10.

Остальные исходные данные (параметры шрифта, инструментарий, характеристики форматирования, шаблоны, словари и т.п.) вводятся по мере проведения исследования.

4 Анализ полученных экспериментальных данных

Анализ данных предполагает их формализацию с целью получения математической модели.

4.1 Графический анализ

В качестве первого шага анализа предлагается представить полученные данные в виде диаграмм, воспользовавшись для этого, например MS Excel. Диаграммы должны отражать вид зависимости удельной памяти и приведенной удельной памяти:

a)  от количества страниц (u = F₁(i), pu = F₂(i));

b)  от количества символов (u_i = F₃(S_i), pu_i = F₄(S_i)).

Виды зависимостей представлены на рис. 2, рис. 3, рис. 4 и рис. 5 соответственно.

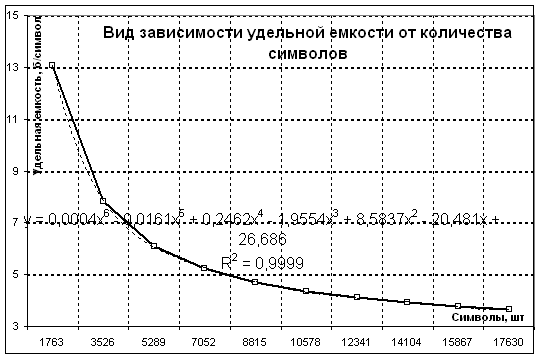
Рис. 2. Реальная зависимость удельной емкости от количества символов.

Из диаграммы рис. 2 следует, что зависимость удельной емкости асимптотически стремится к значению u = 3, достаточно плотно прилегая к значению «три» уже при 17000 символах.

Дальнейший графический анализ студенту предлагается выполнить самостоятельно.

4.2 Упрощенная математическая модель

Любая модель предполагает внесение ограничений. Поэтому предлагается ввести некоторые ограничения заранее, чтобы вскрыть наиболее влияющие факторы, определяющие наиболее существенные зависимости.

4.2.1 Количество символов на странице можно зафиксировать, принимая по 30 строк на страницу и по 80 символов в строке. Ясно, что не удастся так сформатировать текст, чтобы страница имела (30*80 = 2400) 2400 символов. Для приближения к практическим значениям вводится коэффициент К заполнения страницы, и его значение принимается равным 0,75 (К = 0,75). Тогда на гипотетическую страницу придется 1800 символов.

Принимается, что все страницы имеют по 1800 символов.

4.2.2 Экспериментально установлено, что файл с пустой, незаполненной страницей занимает 19,5 Кб памяти, а файл с одной заполненной страницей (см. табл. 1) занимает 23 Кб. Следовательно, на хранение непосредственно текста требуется (23 – 19,5 = 3,5) 3,5 Кб памяти.

Предполагая, что все страницы равномерно заполняются текстом, для хранения файла из N страниц текста потребуется Z Кб памяти:

Z = 19,5 + 3,5*N,                                                                   (3)

где N – количество страниц текста.

Таким образом, упрощенная математическая модель показывает линейную зависимость объема памяти требуемой для хранения от числа страниц текста. Линия смещена примерно на 20 Кб, то есть при N = 0 потребуется примерно 20 Кб памяти.

Для более детального анализа следует, прежде всего, уточнить значение коэффициента К.

4.2.3 Выводы для рассмотренных способов анализа совпадают: чем больше страниц текста приходится хранить в памяти, тем более эффективно используется память. Начиная примерно с 20 страниц текста смещением в 20 Кб можно пренебрегать, принимая зависимость Z = 3,5*N (Кб).