



Механика жидкостей и газов
Это раздел, описывающий поведение газов и жидкостей.
Допущения при изучении:
1. Газы и жидкости будут рассматриваться как сплошная, легкоподвижная среда (лишаем их молекулярной структуры)
2. Газы в механике жидкостей и газов, считаются идеальными, если их скорости движения не велики (<100 м/с), а давление незначительно отличается от атмосферного.
3. Распределение вещества и теплофизических свойств в объёме жидкости и газа является непрерывным.
P,T,V – основные используемые параметры
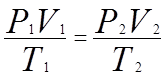
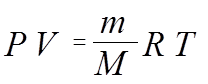
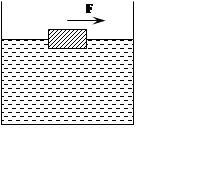 |
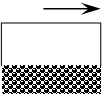 Верхние молекулы тянут за собой
нижние, за счёт молекулярного взаимодействия.
Верхние молекулы тянут за собой
нижние, за счёт молекулярного взаимодействия.

dw – бесконечно малое приращение скорости
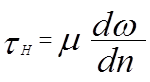
dn – бесконечно малое расстояние
m – коэффициент динамической вязкости
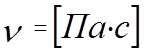
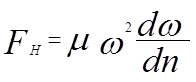
w – площадь соприкосновения слоёв.
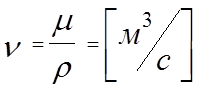 –
коэффициент кинематической вязкости.
–
коэффициент кинематической вязкости.
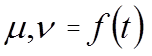
Чем t, тем ниже вязкость жидкостей за счёт уменьшения межмолекулярного взаимодействия.
Чем t, тем выше вязкость газов, т.к. большое количество молекул переходит из одного энергетического состояния в другое.
Уравнение для определения (m) для газов:
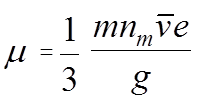 где
m – масса молекулы газа
где
m – масса молекулы газа
nm – число молекул газа
![]() –
средняя скорость движения молекул
–
средняя скорость движения молекул
e – длина свободного пробега (средняя) g=9,8 м/с2
! чем t, тем ![]() и e Þ m
и e Þ m
Статика жидкостей и газов.
Если газ и жидкость находятся в состоянии покоя, то это статическое положение газа или жидкости.
Две группы сил:
1.
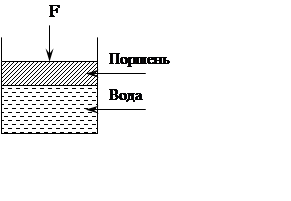 |
2. Массовые силы: пропорциональны массе газа или жидкости (создание статического давления (давление атмосферное))
Каждая материальная точка имеет независящую от координат ориентацию сил, отсюда статическое давление распространяется во все стороны равномерно.
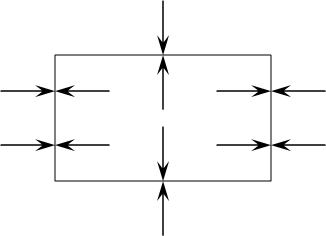 |
Кинематика жидкостей и газов.
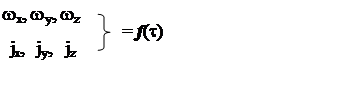 |
j – ускорение газов и жидкостей
w и j – векторные величины
Поведение потока может быть описано двумя способами:
1. Способ Лагранжа:
По Лагранжу, указывается поведение каждой частицы в каждый момент времени.
2. Способ Эйлера:
Выбираем систему координат, какую-то сетку и описываем, что происходит в каждой из точек этой координатной сетки.
Стационарное или установившееся движение:
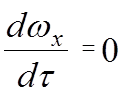
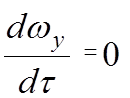
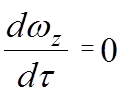
В любой точке потока скорость не изменяется по времени, но может изменяться по координатам.
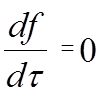 и
др. примеры
и
др. примеры
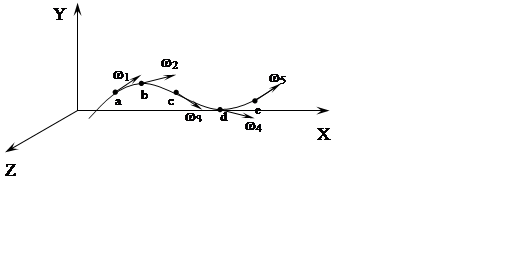
“b” расположена бесконечно близко к точке “a”
“c” расположена бесконечно близко к точке “b”
и т.д.
Получим ломаную линию
Если расстояние между ними (f,b,c,….) сводить к нулю, то будет кривая – называемая линией тока. Каждая частица, находится на линии тока имеет скорость, находящуюся на касательной, находящейся на этой линии тока.
Для нестационарного потока линии тока фиксирует скорость, и положение частицы только в единичный момент времени.
В другой момент времени линия тока будет совсем другой.
Это можно установить на весь поток.
Для случая стационарного давления линии тока будут совпадать с траекториями движения частиц.
Выделим внутри движущегося объёма жидкости или газа бесконечно малый замкнутый контур. Это контур будет ограничен линиями тока для бесконечно маленького промежутка времени (труба тока).
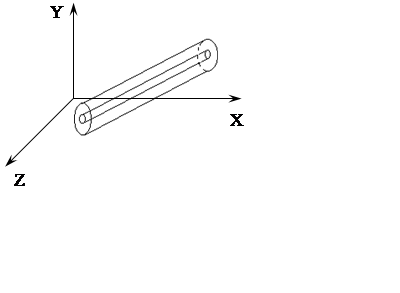
Трубка тока – ото поверхность, ограниченная линиями тока и есконечно малым
сечением.
В разные моменты времени будут разные трубки тока для нестационарного потока.
Для нестационарного потока:
1. Форма элементарной трубки тока остаётся неизменной (с течением времени)
2. Поверхность элементарной струи тока является непроницаемой для частиц среды текущей в этой трубке и для частиц среды в соседних трубках.
3. Из-за бесконечно малого сечения считаем, что скорость среды внутри бесконечно малой струи не изменяется.
(уравнение кинематики)
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.