Решение задач целочис­ленного линейного программирования на ЭВМ, страница 8

Т.к. (в табл. 2)  Vj = 0, дальнейших преобразований делать не нужно. Попробуем определить назначение среди нулевых элементов:

	1	2	3	4	5	6	7	8
1	(0)	2	4	1	7	5	8	3
2	1	3	5	2	2	7	1	(0)
3	4	3	2	1	(0)	8	7	6
4	(0)	1	2	3	4	5	6	7
5	5	6	7	3	(0)	4	2	2
6	0	(0)	1	1	2	2	3	4
7	0	0	0	(0)	0	0	0	0
8	0	0	(0)	0	0	0	0	0

Поскольку у нас как 1 и 4, так 5 и 3 претендуют на одно место, ОП не получится. Поэтому перечеркнем все нулевые элементы минимальным количеством горизонтальных и вертикальных линий. Среди элементов, оказавшихся не перечеркнутыми, выбираем наименьший и вычитаем его из них. А ко всем элементам, перечеркнутым дважды, прибавляем выделенный элемент. Переходим к табл. 4

                     табл.3

	1	2	3	4	5	6	7	8
1	(0)	1	3	0	7	4	7	3
2	1	2	4	1	2	6	0	(0)
3	4	2	1	0	(0)	7	6	6
4	0	(0)	1	2	4	4	5	7
5	5	5	6	2	(0)	3	1	2
6	1	(0)	1	1	3	2	3	5
7	1	0	(0)	0	1	0	0	1
8	1	0	0	(0)	1	0	0	1

В новой таблице (т.4) вновь пробуем ЗН. Т.к. как и в предыдущем варианте ЗН не выполняется – аналогично переходим к табл. 5

                       табл. 4

	1	2	3	4	5	6	7	8
1	0	2	3	(0)	8	4	7	3
2	1	3	4	1	3	6	0	(0)
3	4	3	1	(0)	1	7	6	6
4	(0)	1	1	2	5	4	5	7
5	4	5	5	1	(0)	2	0	1
6	0	(0)	0	0	3	1	2	4
7	1	1	(0)	0	2	0	0	1
8	1	1	0	0	2	0	(0)	1

В новой таблице (т.5) вновь пробуем ЗН. Т.к. 3 и 1 претендуют на одно место, мы ищем другой ОП. Переходим к табл. (6)

                        табл. 5

	1	2	3	4	5	6	7	8
1	(0)	1	2	0	7	3	6	2
2	2	3	4	2	3	6	0	(0)
3	4	2	0	(0)	0	6	5	5
4	0	(0)	0	2	4	3	4	6
5	5	5	5	2	(0)	2	0	1
6	1	0	(0)	1	3	1	2	4
7	2	1	0	1	2	0	(0)	1
8	2	1	0	1	2	(0)	0	1

В табл. 6 нулевые элементы таковы. Что можно найти даже альтернативный ОП, поэтому мы представили табл. 6 в виде таблиц 6.1 и 6.2, показывающие два различных ОП

                           табл.  6.1

	1	2	3	4	5	6	7	8
1	0	1	2	(0)	7	3	6	2
2	2	3	4	2	3	6	0	(0)
3	4	2	(0)	0	0	6	5	5
4	(0)	0	0	2	4	3	4	6
5	5	5	5	2	(0)	2	0	1
6	1	(0)	0	1	3	1	2	4
7	2	1	0	1	2	(0)	0	1
8	2	1	0	1	2	0	(0)	1

                    табл.  6.2

По полученным таблицам составим матрицы:

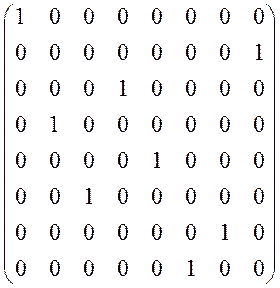Х =              Х=

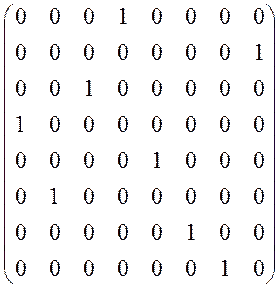
Z = 1 + 1 + 2 + 2 + 2 + 3 + 0 + 0 = 11          Z = 2 + 1 + 3 + 1 + 2 + 2 + 0 + 0 = 11