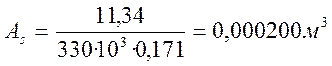
Определяем количество стержней арматуры:
,
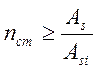где nст – целое число стержней
Аs1 – площадь сечения одного стержня
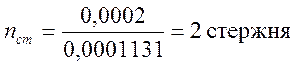
Так как расстояние между стержнями рабочей арматуры плиты не должно превышать 15 см, то принимаем nст = 7 стержней.
С учетом принятого количества стержней определяем высоту сжатой зоны:
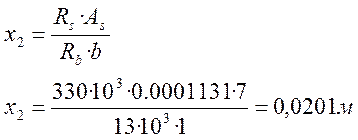
Проверка прочности сечения по изгибающему моменту:
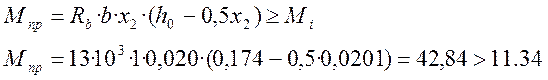
Проверка выполняется.
2.2.2 Расчет на выносливость
Расчет на выносливость производят, считая, что материал конструкции работает упруго.
Бетон растянутой зоны в расчете не учитывается.
Минимальные напряжения в сжатой зоне бетона и растянутой арматуре сравниваются с соответствующими расчетными сопротивлениями.
Расчетные сопротивления материалов устанавливаются в зависимости от характеристики цикла действующих напряжений.
,
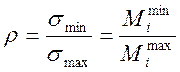где Мmini и Мmaxi – минимальный и максимальный момент от нормативных нагрузок при расчете на выносливость.
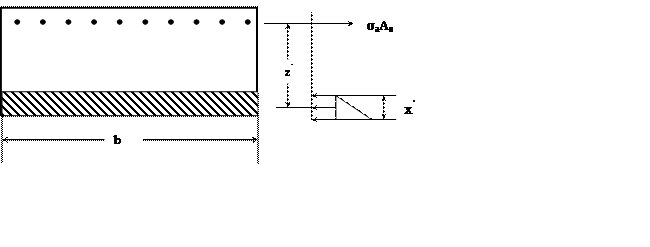
Высота сжатой зоны бетона приведенного сечения определяется по формуле:
,
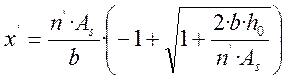где n’ = Es/Eb – условное отклонение модулей упругости арматуры и бетона, при котором учитывается виброползучесть бетона. Для бетона В25 n’ = 20.
.
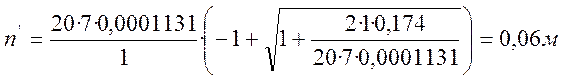Плечо пары внутренних сил при треугольной эпюре сжимающих напряжений в бетоне:
.
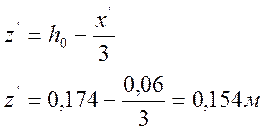Проверка напряжений производиться по следующим формулам:
,
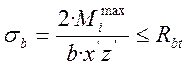где Rbt – расчетное сопротивление бетона сжатию в расчетах на выносливость.
,
где bb – коэффициент, учитывающий рост прочности бетона во времени и принимаемый в зависимости от класса бетона. Для В25 равен 1,34.
eb – коэффициент, учитывающий асимметрию цикла напряжений в арматуре и принимаемый в зависимости от значения r, для r = 0,5 равен 1,2.
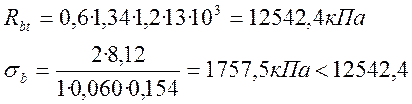- условие выполняется.
,
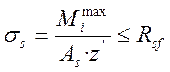где Rsf – расчетное сопротивление арматуры растяжению в расчетах на выносливость.
,
где brw – коэффициент, учитывающий влияние на условия работы арматуры наличия сварных стыков. Для соединений стержней контактной и точечной сваркой при условии механической зачистки их концов равен 1,0.
ers – коэффициент, учитывающий асимметрию цикла напряжений в арматуре и принимаемый в зависимости от значения r и класса арматуры, для r = 0,5 и А-III равен 0,76.
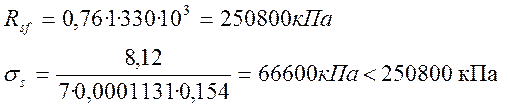
Условие выполняется.
2.2.3 Расчет на трещиностойкость
Расчетом ограничивается ширина раскрытия поперечных трещин.
Определение ширины раскрытия поперечных трещин в конструкциях с арматурой периодического профиля производиться по формуле:
,
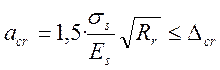где Dcr = 0,02 см – предельное значение расчетной ширины раскрытия трещины.
σs – напряжение в рабочей арматуре
,
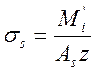где М’I – изгибающий момент в расчетном сечении.
z – плечо пары внутренних сил, принимается из расчета сечения на прочность.
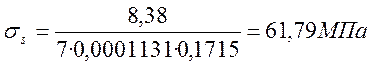
Еs – модуль упругости напрягаемой арматуры. Для А-III равен 1,96·105 МПа
Rcr – радиус армирования
,
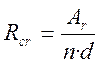где Аr – площадь зоны взаимодействия арматуры с бетоном
n – число стержней рабочей зоны арматуры
d – диаметр арматуры
.
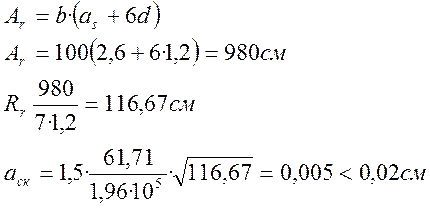Условие выполняется.
2.2.4 Расчет наклонных сечений плиты на прочность.
Проверка прочности по поперечной силе наклонных сечений плиты производиться из условия, ограничивающего развитие наклонных трещин:
,
где Qi – поперечная сила в расчетном сечении
Rbt – расчетное сопротивление бетона осевому растяжению
Проверка выполняется – поперечное армирование не требуется.
3. Расчет главных балок пролетного строения.
3.1 Определение расчетных усилий
Постоянная нагрузка на пролетное строение складывается из собственного веса конструкции и веса мостового плотна.
Нормативная нагрузка на 1 погонный метр главной балки определяется:
,
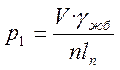где V и lп – объем железобетона и полная длина пролетного строения
n – число главных балок
.
,
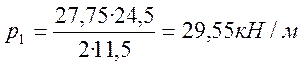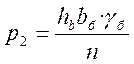где hб – толщина слоя балласта
bб – ширина балластного корыта. Для однопутных мостов принимается 3,6 м.
.
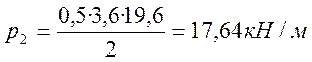Коэффициенты надежности по нагрузке gf1 для постоянных нагрузок при расчете на прочность принимаются:
При расчете на прочность нормативная временная нагрузка на одну главную балку принимается равной:
,
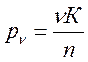где n - эквивалентная нагрузка класса К = 1
К – класс заданной нагрузки
lр – 10,80 м
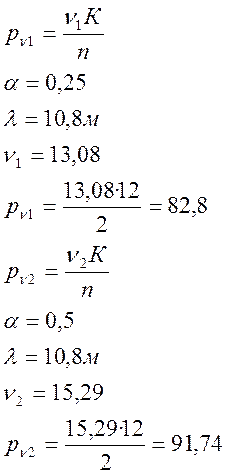
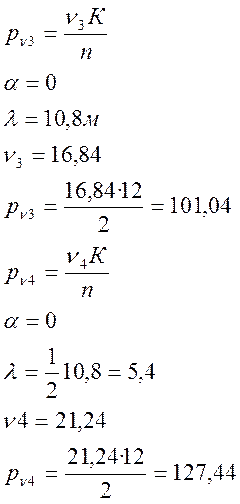
Нормативная временная нагрузка на одну главную балку определяется для участков линий влияния.
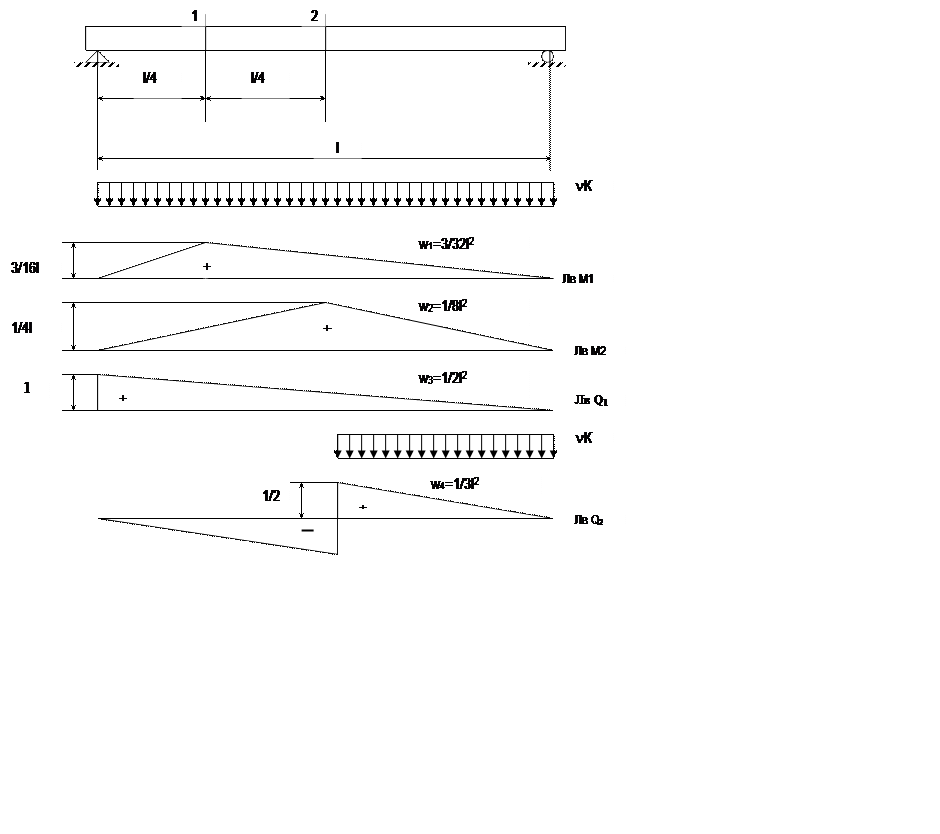
Полные усилия в сечениях разрезной балки при расчете на прочность определяется с учетом всех требований по следующим формулам:
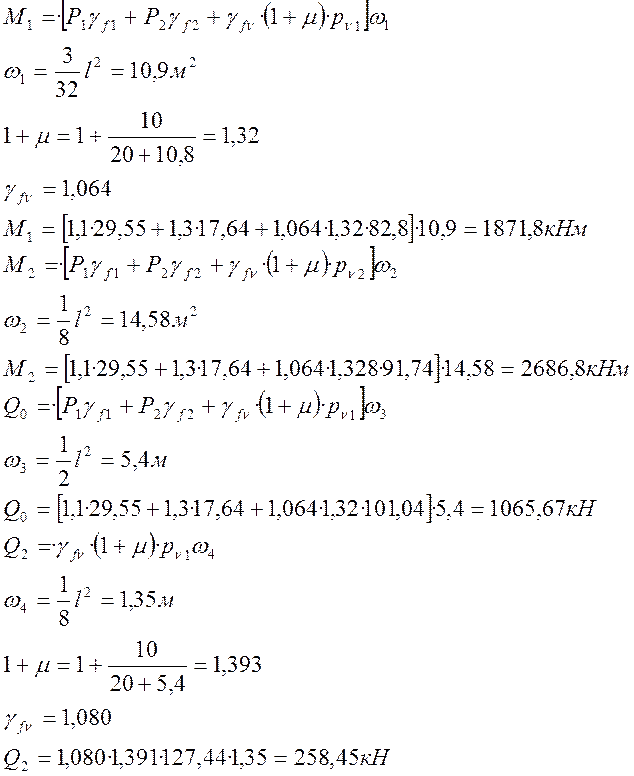
Усилия при расчете на трещиностойкость определяются от действия на конструкцию нормативных нагрузок. Коэффициенты надежности gf1=gf2=gfn=1,0.
Динамический коэффициент 1+m = 1,0.
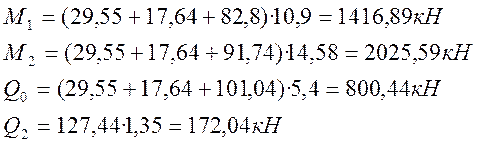
По результатам расчета строят эпюры М и Q.
|
3.2 Расчет балки из обычного железобетона
3.2.1 Расчет на прочность по изгибающему моменту
Выбранный тип поперечного сечения плитный.
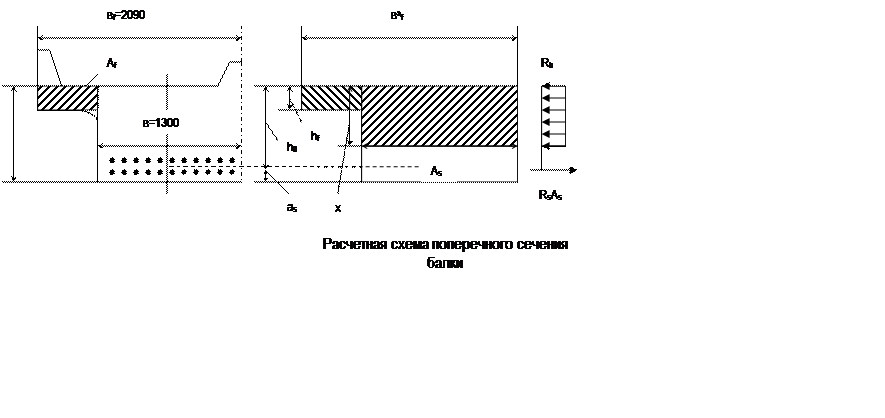
Приведенная (средняя) толщина плиты при фактической ширине плиты вf равна:
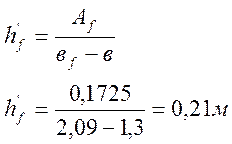
Расчетная ширина сечения плиты не должна превышать значения:
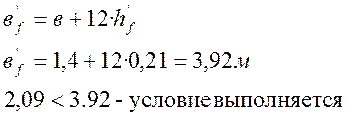
Длина свесов плиты между соседними балками не должна быть больше 0,5(В-в), где В – расстояние между осями главных балок.
0,5(1,3-1,3)=0, так как плитное пролетное строение.
hб = 0,70 м при lП = 11,5 м.
Назначаем аs = 0,16 м от нижней грани пояса балки.
Тогда h0 = hб - аs
h0 = 0,70-0,16=0,54 м,
где аs – центр тяжести арматуры.
Определяем в первом приближении величину сжатой зоны бетона:
.
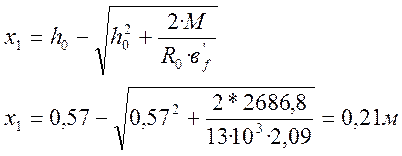Так как 
> x1
, то сечение работает как прямоугольное и количество арматуры определяется по
формуле:
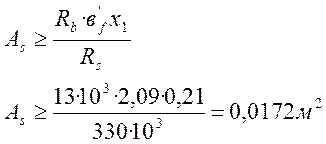
Задаваясь диаметром арматуры определяем количество стержней:
.
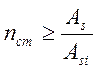Определим площадь одного стержня диаметром 32 мм:
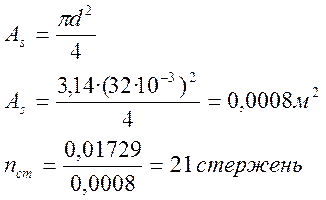
Принимаем 21 стержень. Уточняем значение Аs:
С учетом принятого диаметра и количества стержней, а также после уточнения Аs находим точную величину сжатой зоны:
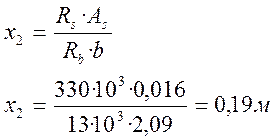
Условие прочности сечения по изгибающему моменту записываем в виде:
,
где z – плечо пары сил
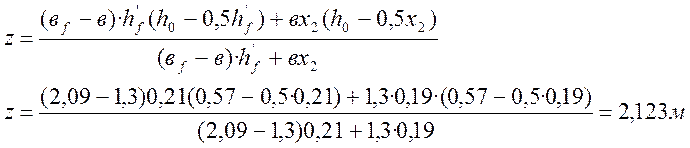
- условие выполняется.
3.2.2 Расчет на трещиностойкость по касательным напряжениям.
Расчет по касательным напряжениям выполняют в предположении упругой работы конструкции, но без учета бетона растянутой зоны.
Касательные напряжения могут быть определены по формуле:
,
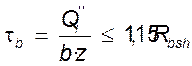где Q’’I – поперечная сила в рассматриваемом сечении от нормативных нагрузок;
b – толщина ребра балки;
z – плечо пары внутренних сил из расчета на прочность по изгибающему моменту;
Rb,sh – скалывание при изгибе, для В25 – 2,5 МПа
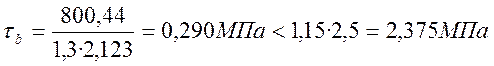- условие выполняется.
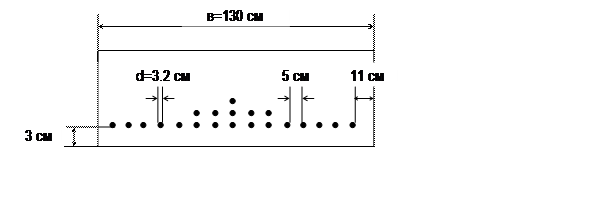
Расположение арматуры
3.2.3 Расчет на прочность по поперечной силе.
При расчете на прочность по поперечной силе изгибаемых железобетонных элементов предполагается, что в предельном состоянии образуется наклонная трещина в бетоне, разделяющая элементы на две части. Поперечная сила в наклонном сечении воспринимается отогнутой арматурой, хомутами и бетоном сжатой зоны.
Места отгибов стержней рабочей арматуры согласуем с эпюрой действующих в балке изгибающих моментов.
Предельный момент, воспринимаемый сечением с одним стержнем рабочей арматуры:
,
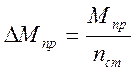где nст – количество стержней рабочей арматуры в среднем сечении:
.
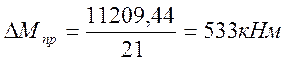Проверка прочности наклонного сечения на действие поперечной силы производиться из условия:
,
где Q – максимальное значение поперечной силы от внешних нагрузок, расположенной по одну сторону от наклонного сечения;
Rsw – расчетное сопротивление арматуры отогнутых стержней;
Аsi , Аsw – площади поперечного сечения соответственно одного отогнутого стержня и всех ветвей одного хомута пересекающих наклонное сечение.
,
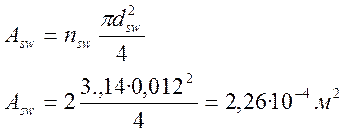при dsw = 12 мм – диаметр хомутов, nsw – число ветвей одного хомута.
Qb – поперечное усилие, передающее на бетон сжатой зоны сечения.
,
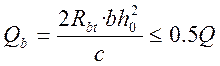где с – длина горизонтальной проекции сечения
На приопорных участках:
с = h0 – x = 0,57 – 0,19 = 0,38 м
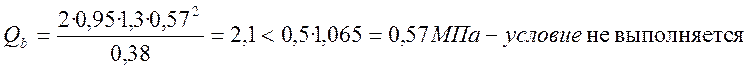
В середине участка:
с = 2h0 = 2·0,57 = 1,14 м
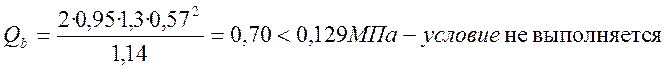
Располагаем схемой, определяя по ней количество отогнутых стержней попавших в сечение (наклонные):
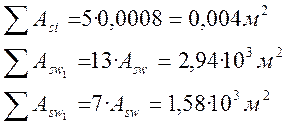
На приопорной части:
- условие выполнено.
В середине пролета
- условие выполнено.
Список литературы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.