Л А Б О Р А Т О Р Н А Я Р А Б О Т А №71д
Распределение Больцмана
Цель работы: изучение распределения частиц воды, получаемых методом ультразвуковой кавитации, в гравитационном поле Земли.
Введение
Известно, что равновесные
распределения могут установиться при действии внешних потенциальных сил.
Например, под действием гравитационной силы молекулы атмосферы Земли стремятся
опуститься на Землю, но тепловое движение препятствует их осаждению. В
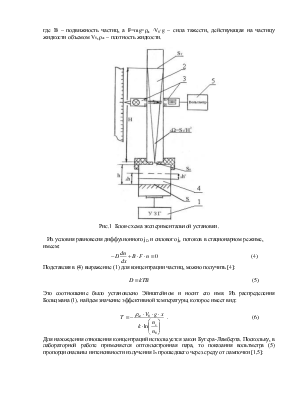
результате устанавливается некоторое равновесное распределение по высоте 
концентрации 
молекул
в потенциальном силовом поле, которое описывается формулой Больцмана 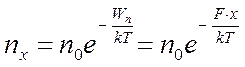[1]:
,
(1)
где 
-
концентрация молекул на поверхности земли, F=mg – сила тяжести, Wn
– потенциальная энергия молекул на высоте ,
Т – эффективная температура, k – постоянная Больцмана.
Методика эксперимента и экспериментальная установка
В настоящей работе методом оптической локации исследуется распределение частиц воды в гравитационном поле Земли. Вертикальный столб частиц воды можно получить с помощью ультразвукового генератора (УЗГ) ((1) рис.1). Частицы воды диаметром около 100 мкм получаются методом акустической (ультразвуковой) кавитации [2,3]. Интенсивная ультразвуковая волна, распространяющаяся в жидкость, налитую в ячейку (4), создает области высокого гидростатического давления. В этих местах возникают кавитационные пузырьки на так называемых кавитационных зародышах, которыми чаще всего являются газовые включения в жидкости и на поверхности ультразвукового излучателя. Захлопывание пузырьков сопровождается адиабатическим нагревом газа в пузырьках до температуры порядка 104 0С. Акустическая кавитация разрушает связи между молекулами жидкости. Частицы из ячейки вылетают в вертикальном направлении через отверстие S0. Стеклянная трубка (2) сечением ST ограничивает пространство, заполненное частицами.
Оптоэлектронная пара (лампочка-фотодиод (3) рис.1) позволяет измерить ослабление света лампочки за счет прохождения через стеклянную трубку, заполненную частицами, на различных высотах. Концентрация частиц, обратно пропорциональна прозрачности столба [4]. Сигнал с фотодиода регистрируется вольтметром (5).
Рассмотрим случай стационарной работы генератора. В этом случае имеют место два процесса. Во-первых диффузионный поток jD частиц из ячейки (4) в вертикальном направлении происходит по закону [4,5]:
,
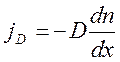(2)
где D – коэффициент диффузии. Во-вторых, встречный поток jс частиц в постоянном и однородном силовом потенциальном поле Земли определяется выражением [4,5]:
,
(3)
где В – подвижность частиц, а F=mg=ρж ∙V0∙g – сила тяжести, действующая на частицу жидкости объемом V0, ρж – плотность жидкости.
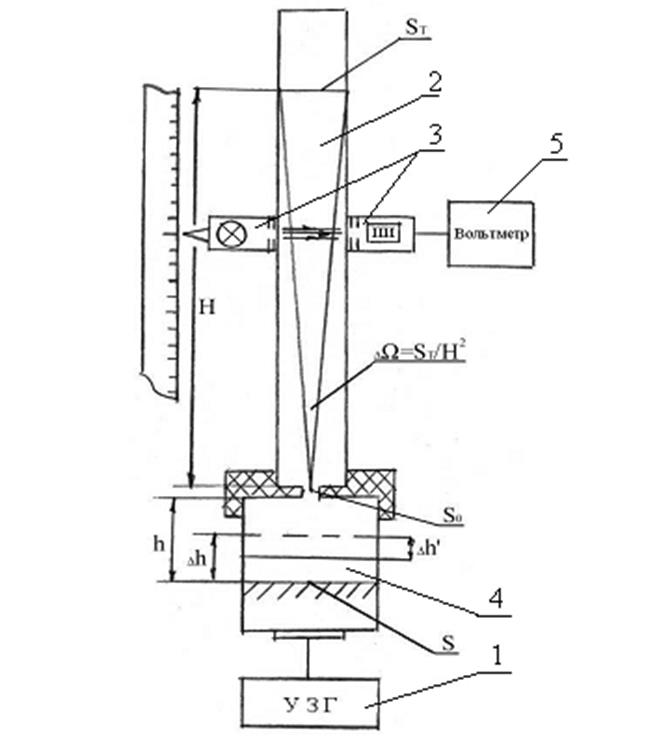
Рис.1 Блок-схема экспериментальной установки.
Из условия равновесия диффузионного jD и силового jс потоков в стационарном режиме, имеем:
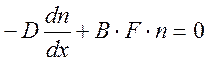(4)
Подставляя в (4) выражение (1) для концентрации частиц, можно получить [4]:
(5)
Это соотношение было установлено Эйнштейном и носит его имя. Из распределения Больцмана (1), найдем значение эффективной температуры, которое имеет вид:
.
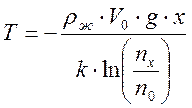(6)
Для нахождения отношения концентраций используется закон Бугера-Ламберта. Поскольку, в лабораторной работе применяется оптоэлектронная пара, то показания вольтметра (5) пропорциональны интенсивности излучения Ix прошедшего через среду от лампочки [1,5]:
,
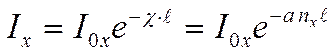(7)
где 
–
показатель поглощения, 
– константа (закон Бера)
[1], 
– расстояние пройденное излучением, I0х – интенсивность входного излучения. Выразим из
(7) концентрацию частиц:
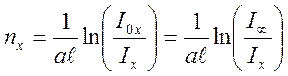. (8)
Величину 
удобно
определить в результате измерений на высоте, где концентрацией частиц можно
пренебречь. Такой способ позволяет учесть прозрачность колбы и геометрические
параметры установки. В работе 
лучше измерить до
заполнения трубки молекулами воды.
Используя (8), получаем выражение для логарифма отношения концентраций:
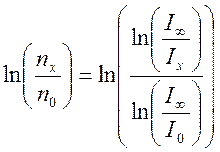. (9)
где 
- интенсивность
прошедшего света на нулевой высоте. С учетом (9), формула (6) принимает вид:
,
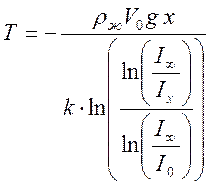(10)
В настоящей работе, измеряя интенсивность прошедшего
света, по формуле (9) вычисляют логарифм отношения концентраций по высоте трубки. Затем строится график этой
зависимости, из линейной части которого находится коэффициент
пропорциональности γ:
,
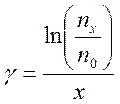(11)
и затем вычисляется эффективная температура частиц воды:
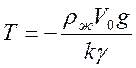. (12)
Конструкция установки
Экспериментальная установка выполнена в виде двух модулей. Первый модуль включает в себя стеклянную трубку, укрепленную на вертикальном штативе с линейкой. На штативе также расположена оптоэлектронная пара: лампа-светодиод, заключенные в металлический непрозрачный кожух. Под стеклянной трубкой находится ячейка с водой, установленная на ультразвуковом генераторе. Для регулировки количества частиц в потоке генератор снабжен ручкой «выход». Включение генератора производится тумблером «сеть» на его передней панели.
Второй модуль заключен в металлический кожух, на лицевой панели которого расположены:
- мультиметр для измерения напряжения с фотодиода;
- тумблер «сеть» включения установки с индикацией;
- тумблер включения осветителя «лампа».
Порядок выполнения работы и обработка результатов
1.Перед началом работы проверьте, что ручка «выход» генератора находится в крайнем левом положении, а в стеклянной трубке отсутствуют капли воды. При необходимости перед началом эксперимента трубку следует насухо протереть.
2.Залить исследуемую жидкость в ячейку между двумя рисками.
3.Включить установку тумблером «сеть», и источник излучения тумблером «лампа».
4.Не включая УЗГ измерить интенсивность прошедшего
излучения в верхней части трубки.
5.Включить генератор тумблером «сеть», расположенным на самом генераторе. Постепенно увеличивая поток частиц жидкости ручкой генератора «выход», установить такое их распределение по высоте столба, при котором столб частиц будет занимать всю высоту трубки при минимальной концентрации в верхней ее части.
6.Перемещая вдоль трубки оптико-измерительную систему, по
показаниям вольтметра измерить интенсивности излучения 
на
различных высотах . Полученные данные
записать в таблицу 1.
Таблица 1.
|
Высота столба
|
|
|
|
=
7.Исходя из результатов измерений рассчитать по формуле (9) логарифм отношения концентраций. Данные занести в таблицу 1.
8.Построить график зависимости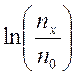 
от
и в линейной области графика
вычислить коэффициент γ по формуле (11).
9.Рассчитать эффективную температуру частиц воды в столбе по формуле (12), считая что средний диаметр частиц составляет d≈100 мкм. Сравнить полученную температуру с температурой жидкости в ячейке и температурой стенок стеклянной трубки.
Контрольные вопросы
1. Запишите аналитическое выражения распределения Больцмана. Поясните физический смысл величин, входящих в это выражение.
2. Равновесием каких потоков частиц устанавливается их распределение в настоящей работе?
3. Применив распределение Больцмана к атмосферному воздуху над поверхностью Земли, получите барометрическую формулу, устанавливающую распределение давления воздуха над поверхностью Земли.
4. В чем состоит закон Бугера-Ламберта?
ЛИТЕРАТУРА
1. Детлаф А.А., Яворский Б.М. Курс физики. М., Высшая школа, 1989.
2. Перник А.Д. Проблемы кавитации. Л., 1966.
3. Кнэпп Р., Дейли Дж., Хэммит Ф. Кавитация. М., Наука,1974.
4. Сивухин Д.В. Общий курс физики. М., Наука, 1983.
5. Савельев И.А. Курс общей физики. М., Астрель, АСТ, 2002.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
