Построение модели динамического программирования для задач различных классов, в которых процесс принятия решений может быть многошаговым

Министерство образования и науки Российской Федерации

Новосибирский государственный технический университет

Кафедра экономической информатики

Отчет

по лабораторной работе №4

«Динамическое программирование»

Вариант №7

Факультет: Бизнеса

Группа:

Студенты:

Преподаватель:

Новосибирск

2004

Цель работы: Научиться строить модели динамического программирования для задач различных классов, в которых процесс принятия решений может быть многошаговым. Правильно определять суть и природу состояний управляемой системы, мероприятий, составляющих управление системой. Приобрести практические навыки и опыт решения многошаговых задач методом динамического программирования.

Задача о ранце

 Требуется загрузить ранец объемом 95 предметами 4 типов. Известен объем каждого предмета v_i и его ценность с_i . Определить, какие предметы и в каком количестве нужно загрузить в ранец, чтобы суммарная ценность груза была максимальной.

V	V1	V2	V3	V4	C1	C2	C3	C4
95	11	9	7	15	520	470	350	640

Параметры состояния:

x₀ = 95,

x₁ = 95-11x₁,

x₂ = 95-11x₁-9x₂,

x₃ = 95-11x₁-9x₂-7x₃,

x₄ = 95-11x₁-9x₂- 7x₃-15x₄.

Уравнения состояний:

x₁ = x₀-11x₁,

x₂ = x₁-9x₂,

x₃ = x₂-7x₃,

x₄ = x₃-15x₄,

Решение:

1. Решение в ПЭР, как задачи динамического программирования.

ИТОГОВОЕ РЕШЕНИЕ   для 132

Элем.     Чис.эл-в  Прибыл    Свободн.пр-во

1           0       0             95

2           9       4230          14

3           2       700           0

4           0       0             0

Сумм.прибыль = 4930

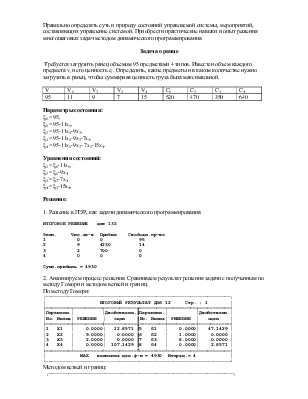
2. Анализируем процесс решения. Сравниваем результат решения задачи с полученным по методу Гомори и методом ветвей и границ.

По методу Гомори:

┌─────────────────────────────────────────────────────────────────┐

│                   ИТОГОВЫЙ РЕЗУЛЬТАТ ДЛЯ 12     Стр. : 1        │

╞═════════╤══════════╤═══════════╦═════════╤══════════╤═══════════╡

│Переменн.│          │Двойственн.║Переменн.│          │Двойственн.│

│No. Имена│ РЕШЕНИЕ  │   оцен    ║No. Имена│ РЕШЕНИЕ  │   оцен    │

╞═════════╪══════════╪═══════════╬═════════╪══════════╪═══════════╡

│1   X1   │    0.0000│   12.8571 ║5   S1   │    0.0000│   47.1429 │

│2   X2   │    9.0000│    0.0000 ║6   S2   │    1.0000│    0.0000 │

│3   X3   │    2.0000│    0.0000 ║7   S3   │    8.0000│    0.0000 │

│4   X4   │    0.0000│  107.1429 ║8   S4   │    0.0000│    2.8571 │

╞═════════╧══════════╧═══════════╩═════════╧══════════╧═══════════╡

│            MAX   величина цел.ф-и = 4930  Итерац.= 4            │

└─────────────────────────────────────────────────────────────────┘

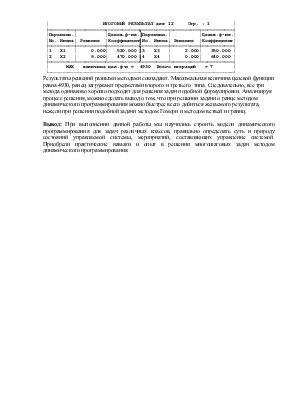
Методом ветвей и границ:

 ┌─────────────────────────────────────────────────────────────────┐

 │                   ИТОГОВЫЙ РЕЗУЛЬТАТ для 12     Стр. : 1        │

 ╞═════════╤══════════╤═══════════╦═════════╤══════════╤═══════════╡

 │Переменн.│          │Целев.ф-ия.║Переменн.│          │Целев.ф-ия.│

 │No. Имена│ Решение  │Коэффициент║No. Имена│ Решение  │Коэффициент│

 ╞═════════╪══════════╪═══════════╬═════════╪══════════╪═══════════╡

 │1   X1   │     0.000│   520.000 ║3   X3   │     2.000│   350.000 │

 │2   X2   │     9.000│   470.000 ║4   X4   │     0.000│   640.000 │

 ╞═════════╧══════════╧═══════════╩═════════╧══════════╧═══════════╡

 │      MAX   величина цел.ф-и =  4930  Всего итераций   = 7       │

 └─────────────────────────────────────────────────────────────────┘

Результаты решений разными методами совпадают. Максимальная величина целевой функции равна 4930, ранец загружают предметами второго и третьего  типа. Следовательно, все три метода одинаково хорошо подходят для решения задач подобной формулировки. Анализируя процесс решения, можно сделать вывод о том, что при решении задачи о ранце методом динамического программирования можно быстрее всего добиться желаемого результата, нежели при решении подобной задачи методом Гомори и методом ветвей и границ.

Вывод: При выполнении данной работы мы научились строить модели динамического программирования для задач различных классов, правильно определять суть и природу состояний управляемой системы, мероприятий, составляющих управление системой. Приобрели практические навыки и опыт в решении многошаговых задач методом динамического программирования.