Опытная проверка закона сохранения импульса методом соударения шаров: Методические указания к лабораторной работе, страница 2

            Равенства (3) и (5) имеют векторный характер. В случае центрального удара, когда векторы всех скоростей , направлены вдоль одной прямой, символы вектров можно опустить и все геометрические суммы заменить алгебраическими, т.е. в равенствах (3) и (5) можно перейти от векторов к их модулям. При этом скорость будем считать величиной положительной, если шар движется справа налево, и отрицательной если слева направо. Если при соударении векторы всех скоростей направлены в одну сторону то равенства (3) и (5) приводят к виду

, (3’)

и

, (5’)

7

В случае соударения шаров одинаковой массы () закон сохранения импульса запишется так: при упругом ударе (см. равенство (3’))

,  (7)

при абсолютно неупругом ударе (см. равенство (5’))

или

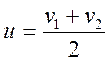, (8)

Соответственно формула (6) для коэффициента восстановления механической (кинетической) энергии примет вид:

При абсолютно упругом ударе

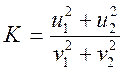,  (9)

При абсолютно неупругом ударе

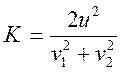 , (10)

8

            Описание экспериментальной установки

            Используемая в данной работе установка ( рис. 1) представляет собой два одинаковых маятника, состоящих из стержней 1 и шаров 2. маятники подвешены на поперечных стержнях, закрепленных в стойке прибора. Длина подвеса может изменяться путем перемещения по поперечным стержням подвижных креплений. Один из стержней закреплен неподвижно, а второй может перемещаться относительно первого при помощи регулировочного винта. Перемещение одного из стержней необходимо для установки шаров на заданном расстоянии друг от друга. Для фиксации шаров в заданных положениях и их пуска служат специальные электромагнитные пускатели.

            Положение шаров фиксируется на двух шкалах с ценой деления 1 мм, расположенных на основании прибора. Нулевые деления шкал, располагающиеся против стойки прибора смещены на расстояние равное сумме радиусов шаров. При необходимости «0» левой шкалы можно смещать в ту или другую сторону, для чего надо отпустить стопорный винт в плоскости крепления шкалы к основанию прибора. Прибор имеет электронную систему измерения времени соударения. На панели прибора имеются три кнопки: «включение», «пуск» и «сброс». После включения прибора в сеть напряжением 220 В и нажатия кнопки «включение» загорается световое табло отсчета времени. При нажатии кнопки «сброс» включается электромагнит удерживающий отклоненный на некоторый угол правый шар. При нажатии кнопки «пуск» электромагнит отключается и шар начинает двигаться вдоль шкалы, проходя по ней до соударения путь . В момент соударения включается счетчик времени удара и в окошке светового табло появляется цифра соответствующая времени

9

совместного движения шаров. После удара шары начинают двигаться в противоположных направлениях. Левый шар проходит путь  , а правый  - путь   

            Пусть в первом случае шар 1 отклонен от положения равновесия на угол  (рис.3). В этом положении он обладает потенциальной энергией

,

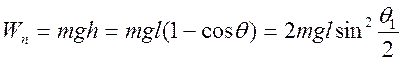где      m- масса маятника;

            g- Ускорение силы тяжести;

            l- длина маятника;

В момент прохождения шара через положение равновесия  его потенциальная энергия полностью превращается в кинетическую. Следовательно, на основании закона сохранения механической энергии можно записать

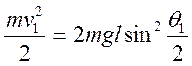
10

Отсюда имеем

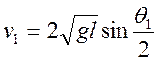    (II)

Напомним, что V – это скорость шара 1 непосредственно перед соударением.

            Обозначив угол отклонения шара 1 от положения равновесия после соударения шаров через  и, воспользовавшись законом сохранения механической энергии, получим аналогичное выражения для скорости  шара 1 непосредственно после соударения

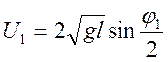 ,  (12)

            После соударения шар 2  на угол   и его скорость непосредственно после соударения

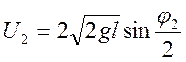,  (13)

            Примем во внимание то, что перед соударением шар 2 был неподвижен () и перепишем формулу (9) в виде:

 

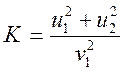
            После подстановки значений скоростей шаров из формул (11), (12) и (13) для упругого удара шаров получим:

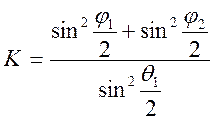 ,  (14)

            Соответственно, для неупругого удара:

11

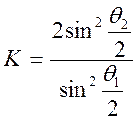 ,   (15)

            где θ - угол отклонения обеих шаров, движущихся после удара как единое тело.

            Примечание. При определении угла θ отклонение находим по положению их точки соприкосновения (т.е. по положению центра масс системы).

Напомним, что мы условились считать скорость положительной величиной при движении шара справа налево и отрицательной – при движении слева направо.

            В соответствии с этим углу θ приписывается знак плюс, если шар отклонен вправо, и минус – если влево, а углу φ приписывается знак плюс, если после удара шар отклонился влево, и минус – если вправо.

            Заметим, что при малых углах отклонения маятника от положения равновесия, угловые меры можно заменить пропорциональными им линейными, т.е. в качестве меры отклонения маятника от положения равновесия брать не угол отклонения подвижного шара от вертикали, а длину дуги, которую описывает центр шара.

Введя обозначения:  ,  ,  ,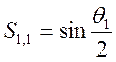 

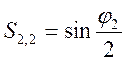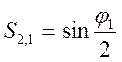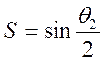
и подставив в формулы (14) и (15) получим:

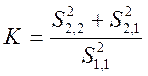,   (16)

12

и             

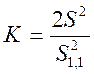,  (17)

где S – смещение двух шаров, движущихся после неупругого удара как единое тело.

            Согласно основному закону динамики импульс силы удара шаров равен приращению импульса одного из шаров

 ()

            Если бы шар 2 во время удара оставался неподвижным (что можно достичь удерживанием его рукой на отметке «0», то шар 1 после удара стал бы двигаться в противоположном направлении со скоростью К (где К – коэффициент восстановления энергии при упругом ударе). Проинтегрировав выражение (*) в пределах от 0 до t и от V до - К, считая что средняя сила удара  <F> за время   t  не изменяется, получим:

            Для вычисления        <F> надо выразить скорость удара V₁  из равенства кинетической энергии и потенциальной энергии 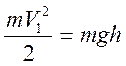, откуда