Определение ошибки измерения времени человеком-оператором: Методические указания к лабораторной работе, страница 2

2.  2. Всю совокупность полученных результатов необходимо проанализировать на наличие грубых ошибок. Таковыми в данном случае следует полагать измерения, при которых t_i получено меньше 0,1 сек и больше 0,45 сек. Эти результаты необходимо отбросить. Среди оставшихся результатов, которых должно оставаться не менее 70, найти наименьшее и наибольшее значения tmin и tmах. Эти значения требуются для построения гистограммы, т.е. ступенчатой кривой, показывающей, сколько результатов измерений t_i попадает в интервал .

Для получения набора результатов измерений .промежуток между t_min и t_max разбивается на К интервалов. При этом величина интервала  определяется следующим образом:

                            

где К согласовывается с преподавателем. Если для имеющихся результатов и согласованного К получится величина Δ >0,0l сек, то в дальнейших расчётах её надо принять кратной 0,01 сек (т.е.0,01, 0.02 или 0,03  и т.д.). При этом количество интервалов К изменится в большую

  5

 или меньшую сторону  по сравнению с величиной К, вы

численной для .

Если величина Δ получится меньше 0,01 сек, то в качестве интервала разбиения Δ принимаю т значение 0,01 сек и из формулы (1) в этом случае определяем число интервалов разбиения:

                       К = (t_min - tmax)/0,01

3. Определив К, производят подсчет числа результатов измерений n_i, попавших в интервал t_i + , т.е.

n₁, таких, что  

таких, что   

, таких что                                 

, таких, что   

При этом должно соблюдаться условие:

              n₁₊ n₂ + n₃ + ...+ n_k = N_Σ

– т.е. полному числу измерений.

4. Построить гистограмму распределения результатов измерений. Для этого по оси абсцисс отложить величину t, а по оси ординат - значения (n_i ) (i - l.,2,3,..., К). Полученная ступенчатая кривая называется гистограммой.

Эта кривая при увеличении числа измерений N и уменьшении интервала Δ стремится к непрерывной зависимости, называемой кривой распределения ошибок и описываемой функцией Гаусса:

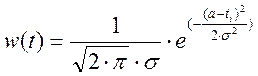                                                             (2)

5. Для полученной гистограммы определить положение максимума на оси абсцисс. Это и будет искомое время задержки (ошибки измерения) Т_э,

6. Из полученной серии измерений найти среднее арифметическое:

                                                                                                  6

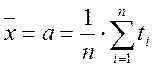                                                                              (3)

6

и дисперсию измерений D = σ²:

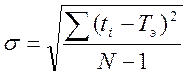                                                           (4)

По полученным значениям а и σ построить кривую Гаусса по формуле(2).

7. Сравнить положения максимума кривой Гаусса, определяемое величиной "а" и максимума гистограммы. Оценить степень расхождения полученных результатов. С этой целью вычислить доверительный интервал для оценки среднеарифметического по методике Стьюдента. Для этого рассчитать вспомогательную величину S:

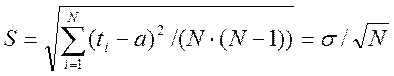                                (5)

Из таблицы коэффициентов Стьюдента найти величину α, зависящую от числа проведенных измерений и выбранной надежности (доверительной вероятности) результатов

Доверительный интервал для величины "а":

                                                                        (6)

Для последующих измерений при работе в лаборатории каждому студенту необходимо пользоваться полученным им значением Т_э = а, найденным по формуле (3) со среднеквадратичным отклонением σ, найденным по формуле (4) .

7

Окончательный результат записать в виде:

                                                             (7)

σ  =  …………….сек                                                            (8)

                                                                                       7

Литература

1.  Дж. Тейлор. Введение в теорию ошибок. М. , "Мир", 1985 г.

2.  Зайделъ А. Н. Ошибки измерений физических величин. Л. ."Наука", 1974 г.

3.  Курушин А. Д. Ошибки измерений физических величин. Вычисление ошибок косвенных измерений. Методические указания для студентов первого курса механических и строительных специальностей. М. , МИИТ , 2004 г .

Приложение 1.

Для удобства построения функции Гаусса ее удобнее переписать в следующем виде:

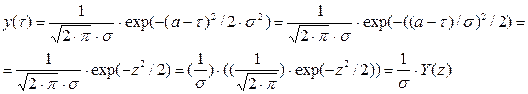     (9)

                                                                                                       8

где обозначено:

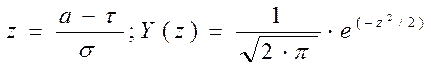                           (10)

Ниже, в таблице 1, приведены значения функций, облегчающих построение зависимостей (2) или (9) .

                                                                                         Таблица 1

Z	00	00.2	00.4	00.6	00.8	11.0	11.5	22.0	22.5
	01	0.98	0.923	0.835	0.726	0.606	0.325	0.135	0.044
Y(z)	0.399	0.391	0.368	0.333	0.290	0.242	0.129	0.054	0.018

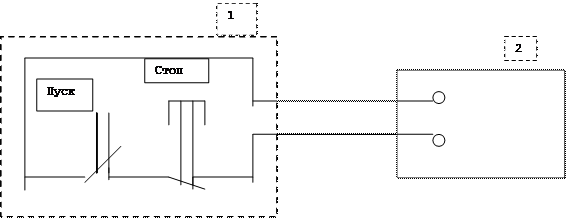
Рис. 1 Схема установки для определения ошибки измерения времени человеком-оператором.

 

I- пульт студентов, 2 - электронный секундомер

 9

                      Приложение 2.

Таблица коэффициентов Стьюдента

Число изме- рений	Доверительная вероятность
	0.7	0.8	0.9	0.95	0.99	0.999
2	2.0	3.1	6.3	12.7	63.7	636.6
3	1.3	1.9	2.9	4.3	9.9	31.6
4	1.3	1.6	2.4	3.2	5.8	12.9
5	1.2	1.5	2.1	2.8	4.6	8.6
10	1.1	1.4	1.8	2.3	3.3	4.8
15	1.1	1.3	1.8	2.1	3.0	4.1
20	1.1	1.3	1.7	2.1	2.9	3.9

                                                     10