Определение момента инерции физического маятника по периоду его малых колебании и приведенной длине, страница 2

Один из методов определения момента инерции маятника относительно оси, проходящей через опорную призму, сводится к определению периода колебаний T маятника относительно этой оси, массы m и расстояния d от центра тяжести до оси (см. формулу (6) для 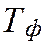). В этом случае момент инерции маятника вычисляется по формуле

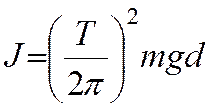                                                       .                                                     (8)

Положение центра тяжести определяется с помощью дополнительной призмы балансировки.

Кроме этого метода, на практике часто используется метод определения момента инерции по приведенной длине физического маятника. Приведенную длину находят из опыта, подбирая такой математический маятник, который колеблется синхронно с данным физическим. Определив длину математического маятника  находят момент инерции по формуле

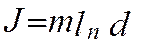                                                                                                                         (9)

4. Таблицы и графики[1].

Таблица 1 Определение периода колебаний маятника

Положение оси вращения	Расстояние от оси вращения до центра тяжести d,м	Время 10 колебаний, с					tср, с	Среднее   значение периода колебаний Тср,с
		1	2	3	4	5
Призма 1
Призма 2

Таблица 2 Определение приведённой длины физического маятника

Положение оси вращения	Расстояние от шарика до точки подвеса, м	Радиус шарика, м	,м
Призма 1
Призма 2

Таблица 3 Расчёт момента инерции физического маятника

Положение оси вращения	Момент инерции физического маятника J, кг·м2
	по методу колебаний	по методу приведенной длины
Призма 1
Призма 2

Таблица 4 Определение погрешностей измерения

Положение оси вращения				кгм2 (метод колебаний)	J кгм2 (метод приведенной длины)
Призма 1
Призма 2

5. Расчёт погрешностей измерений

(указать метод расчёта погрешностей).

1.  Найти и сравнить систематическую и случайную ошибки определения t. Случайную ошибку вычислить по формуле

                                           .

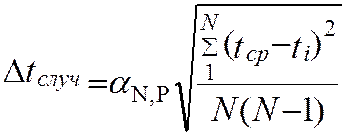Для доверительной вероятности P=0.95 и числа измерений N=5, a=2.8.

Систематическая ошибка определяется классом точности прибора и ошибкой, связанной с конечной скоростью реакции человека, которую можно принять равной 0,1с. В нашем случае непосредственно приборной ошибкой можно пренебречь по сравнению с этой величиной и считать систематическую ошибку равной Δt_сист 0,1с, а полную ошибку рассчитать по формуле

Dt=ÖDt²_сист+D t²_случ.

2. Рассчитать и занести в таблицу 4 относительные ошибки определения величин t, m и d.

3. Рассчитать максимальную абсолютную ошибку определения момента инерции по формуле

                                      .

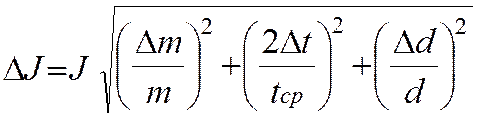Результат определения момента инерции с указанием абсолютной ошибки занести в таблицу 4.

Примечание. Значения величин g и p известны с большой точностью, и следовательно относительные ошибки, вносимые округлением этих величин, могут быть сделаны как угодно малыми, т. е. заведомо меньшими, чем ошибки измерения остальных величин m, d, t. Практически это означает, что при вычислениях значения g и pдостаточно принять равными 9,81 м/с² и 3,14 соответственно.

6. Окончательные результаты:

Подпись студента:

Лист – вкладыш

5. Расчёт погрешностей измерений (продолжение):

7. Дополнительная страница

(для размещения таблиц, теоретического материала и дополнительных сведений).

Первый метод. Подвесив маятник на призме 1 (см. рис.5), отклонить его на небольшой угол (10 градусов) и измерить секундомером время 10 колебаний. Измерения произвести 5 раз. Затем произвести аналогичные измерения, подвешивая маятник на призме 2. Данные занести в табл. 1. Вычислить , а затем найти период по формуле   

.

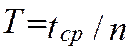Второй метод. Изменяя длину математического маятника, добиться того, чтобы он колебался синхронно с физическим. Полного совпадения периодов обоих маятников добиться нелегко. Поэтому следует, постепенно меняя длину нити математического маятника, добиться того, чтобы маятники колебались синхронно в течение 10—15 колебаний. Измерить расстояние от шарика до точки подвеса. Длина математического маятника равна этому расстоянию плюс радиус шарика (диаметр шарика измеряется штангенциркулем). Ее можно считать приведенной длиной  физического маятника. Результаты занести в табл. 2. Момент инерции вычислить по формуле (9) и результат занести в табл.3.

Подобные измерения и расчеты повторить, подвешивая маятник на второй призме.

Для определения расстояния d от центра тяжести до оси вращения снять маятник с опоры и положить на специальную подставку (призму балансировки). На подставке, которая имеет острую грань, маятник необходимо уравновесить. Расстояние от точки, находящейся над гранью призмы балансировки, до опорной призмы измерить масштабной линейкой с точностью до 0,001 м. Затем рассчитать момент инерции по формуле (8). Результат занести в табл.3.