Определение длины волны света

Условие образования в дифракционной картине главных
максимумов при косом падении света на решетку примет вид

d (sinβ — sin φ _max,n) = пλ                 (8)

где n = 0; ±1; ± 2; ± 3;... —        целое число, определяющее порядок главных максимумов дифракционной картины;
φmax,n— угол дифракции n-го максимума относительно нормали к дифракционной решетке.

Для грубых решеток углы дифракции малы, и равенство (8) можно привести к виду

dcosβ (β —φ_max,n) = nλ,.

Так как β-φmax,n =αmax,n (см. рис. 4), то для главных максимумов получим

dcosβ·α_max,n=nλ, (9)
где α_max,n— угол дифракции n-го максимума, отсчитываемый
относительно направления распространения падающей на решетку волны x'. Величину dβ=dcosβ называют эффективным периодом решетки.

Сравнение условий образования п-го максимума при косом падении света на решетку (9) и нормальном падении (4) показывает, что увеличение угла падения β дает тот же эффект, что и уменьшение периода решетки.

Если в опыте угол β можно выбрать близким к π/2, то эффективный период будет достаточно малым и расстояния между соседними главными максимумами увеличатся. Таким образом на грубой решетке, используя косое падение волн, можно получить отчетливую дифракционную картину.

Следует добавить, что дифракционную картину можно наблюдать, поставив за дифракционной решеткой тонкую собирающую линзу. Экран для наблюдений помещают в фокальную плоскость линзы. Так как линза не вносит дополнительной разности хода (таутохронизм линзы), условия образования максимумов и минимумов освещенности в дифракционной картине записываются в прежнем виде (4), (5), (9), Линза распределит падающий на ее поверхность световой поток по оптическому экрану в соответствии с углами падения световых волн по отношению к главной оптической оси линзы. Дифракционная картина приблизится к решетке, станет более четкой, расстояния между главными максимумами уменьшатся.

Приборы и принадлежности: оптическая скамья; газовый (He-Ne) лазер; дифракционная решетка; мерная линейка; оптический экран с миллиметровой шкалой; тонкая собирающая линза; прикладная телевизионная установка; осциллограф.

36

где δABи δl₂ — абсолютные погрешности соответственно АВ и l₂. Здесь и далее абсолютные погрешности измерений принять равными половине цены деления соответствующих измерительных приборов.

Задание 2. Определение длины волны света

2.1. Установить собирающую линзу 6 между бипризмой и экраном.

2.2. Перемещая линзу вдоль оптической скамьи, добиться четкого изображения на экране двух параллельных линий — действительных изображений источников S1и S₂. Измерить расстояние d’ между ними, а также расстояния а между источником Sи линзой и b — между линзой и экраном, (Плоскость, в которой расположен линейный источник света S,отмечена на установке.)

2.3. Вывести линзу из зоны перекрытия волн. Не меняя положения экрана на оптической скамье, измерить ширину интерференционной полосы Δx, взяв расстояние hмежду тремя-пятью полосами и поделив его на число N светлых полос между ними. Оценить относительную погрешность измерения

где    l = l1+ l₂.

Оценить относительную  погрешность измерения λ:

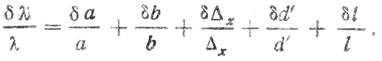
2.5. Определить длину световой волны другим способом. Из формул (6), (8) и (9) находим                                    (11)

                                                                                                  9