Измерение вязкости жидкости: Методические указания к лабораторной работе, страница 2

Рис. 2

1)  сила тяжести Р, направленная вертикально вниз и равная

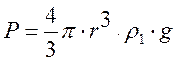        (1)

(где r – радиус шарика,  - плотность материала шарика при данной температуре; g – ускорение свободного падения).

2)  сила Архимеда F_A, направленная вертикально вверх и равная весу жидкости, вытесненной шариком,

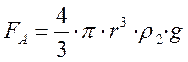          (2)

(где  - плотность жидкости при данной температуре).

3)  сила внутреннего трения F_трнаправлена в сторону, обратную скорости движения (в нашем случае вертикально вверх); ее можно рассчитать по формуле Стокса:

           (3)

(где V– скорость равномерного движения шарика;  - коэффициент внутреннего трения).

Силы Pи F_A постоянны, а F_тррастет с увеличением скорости шарика. Это происходит до тех пор, пока равнодействующая всех сил не станет равной нулю:

.       (4)

Начиная с этого момента шарик движется равномерно.

Подставляя (1), (2) и (3) в уравнение (4), получим условие равномерного движения шарика в виде:

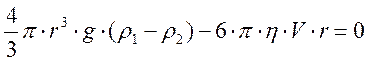
Заменив в полученном соотношении радиус шарика на его диаметр 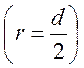, а скорость установившегося движения шарика по отношению пройденного пути l к затраченному на его прохождение времени 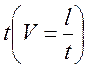, получаем окончательное выражение для расчета коэффициента вязкости жидкости:

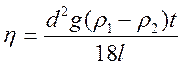     (5)

Уравнение (5) справедливо для случая, когда шарик падает в безграничной среде. Если шарик движется вдоль оси трубки, то необходимо учитывать влияние стенок трубки. Это влияние обусловлено тем, что молекулы слоя жидкости, прилегающие к внутренним стенкам трубки, «прилипают» к ней и не перемещаются.

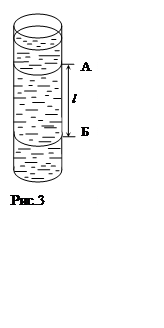Вискозиметр, используемый в данной работе (рис.3), представляет собою стеклянный цилиндрический сосуд, закрепленный в держателе и расположенный строго вертикально. Нижний конец сосуда запаян, а на верхнем имеется воронка с отверстием строго по осевой линии цилиндра, предназначенная для зарядки вискозиметра исследуемой жидкостью и для придания направления движения твердых шариков, опускаемых в жидкость. На цилиндре имеются две метки (А и Б), способные перемещаться вдоль него. Внутренний диаметр вискозиметра значительно превосходит диаметр маленьких твердых шариков, поэтому влиянием вискозиметра на их движение можно пренебречь.

Наблюдая за характером равномерного движения шарика в жидкости и используя соотношение (5), можно определить коэффициент внутреннего трения жидкости.

Порядок работы

и обработки результатов измерений

1.  Отобрать для опыта пять шариков;

2.  Измерить диаметр каждого шарика три раза в различных направлениях и данные измерений занести в табл. 1;

3.  Измерить расстояние между метками на вискозиметре с точностью до 1 мм;

Таблица 1

Номер шарика	Диаметр шарика d, см.			Средний диаметр шарика dср, см
	1	2	3
1
2
3
4
5

4.  Опустить шарик в вискозиметр через воронку и измерить время его движения между метками;

            Измерение повторить для каждого из пяти шариков. Данные опыта занести в таблицу 2.

Таблица 2

Номер шарика	dср, см	l, см.	t, с.	h, Па·с
1
2
3
4
5
			hср=

5.  Вычислить коэффициент внутреннего трения по результатам каждого опыта. Определить среднее значение этого коэффициента.

П р и м е ч а н и е.  При проведении опытов фиксируются: наименование жидкости, ее плотность, температура окружающей среды и плотность материала шарика.

Оценить абсолютную погрешность измерения коэффициентов вязкости по методу Стьюдента.

Для этого необходимо найти

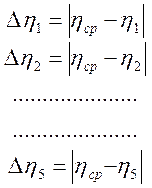
и вычислить вспомогательную величину

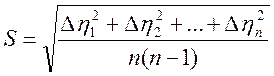
где n – число измерений коэффициента вязкости.

Затем вычислить абсолютную погрешность по формуле

где а – коэффициент Стьюдента, равный 2.8 для доверительной вероятности =0.95 при n=5.

Окончательный результат записать в виде

Контрольные вопросы.

1. В чем заключается физическая природа вязкости?
2.  При каких условиях сила внутреннего трения пропорциональна скорости?
3. Объясните характер зависимости коэффициента внутреннего трения от температуры?
4. Напишите размерность коэффициента трения.
5. Каков характер изменения скорости и ускорения шарика на всем пути его движения?
6. Как изменяется скорость падения парашютиста при затяжном прыжке?

Литература

1. Савельев И.В. Курс общей физики, т.2..М.: Наука, 1987
2. Матвеев А.Н. Молекулярная физика. М.: Высшая школа, 1981
3. Кикоин А.К. Молекулярная физика. М.: Наука, 1982

Содержание

Цель работы………………………………………………..	3
Введение……………………………………………………	3
Описание установки и методика измерения……………..	5
Порядок выполнения работы и результаты измерений…	8
Контрольные вопросы…………………………………….	10
Литература…………………………………………………	10