Математические формулы, используемые при формализации разветвляющихся вычислительных процессов

Приложение 2

Математические формулы, используемые при формализации разветвляющихся вычислительных процессов

Структура Развилка

2. Уравнение прямых в общем виде:

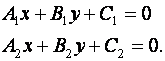
Условие перпендикулярности двух прямых записывается в виде

.

4. Квадрат можно описать окружностью, если диагональ квадрата меньше диаметра окружности или равна ему. Необходимо выразить диагональ квадрата и диаметр окружности через заданные площадь квадрата и длину окружности.

; L = pD

6. Две точки с координатами (x₁, y₁) и (x₂, y₂) лежат на одной окружности с центром в начале координат, если длины радиусов-векторов, соединяющих эти точки с началом координат, равны. Проверку на равенство осуществлять с заданной точностью. Длина радиус-вектора определяется как расстояние между двумя точками с координатами (0, 0) и (x,y).

         Расстояние d от точки до начала координат определяется по формуле

.

8. Чтобы круг поместился в квадрат, диаметр круга должен быть меньше стороны квадрата или равен ей.

10. Точка с координатами (x, y) лежит на окружности радиуса R, если , где e – точность, с которой осуществляется проверка на равенство.

12. По трем сторонам с длинами a, b иc можно построить треугольник, если . При вводе длин сторон должно соблюдаться условие ().

14. Точка с координатами (x, y) попадает в кольцо, если .

16. Окружность пересекает заданную, если выполняется неравенство: , где x,y – координаты центра второй окружности.