Его решениями являются выражения (1.1).
П р и м е р
3. Дифференциальное уравнение незатухающих гармонических колебаний имеет
вид 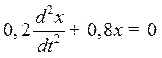 . Найти частоту и период этих
колебаний.
. Найти частоту и период этих
колебаний.
Р е ш е н и е.Запишем уравнение в виде: 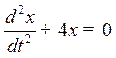 .
.
 Отсюда следует, что
Отсюда следует, что ![]() а
а ![]() Период
колебаний определяется по формуле:
Период
колебаний определяется по формуле: ![]() Следовательно, Т
= 2∙3,14/2 = 3,14 с.
Следовательно, Т
= 2∙3,14/2 = 3,14 с.
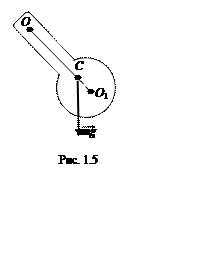
Физическим маятником называют твёрдое тело, которое совершает колебания под действием силы тяжести вокруг неподвижной горизонтальной оси (рис. 1.5), проходящей через точку О, не совпадающую с центром масс С тела.
Момент силы тяжести mg относительно оси вращения О
![]() ,
,
где ![]() - длина физического маятника
(pасстояние от точки подвеса до центpа масс маятника
- длина физического маятника
(pасстояние от точки подвеса до центpа масс маятника ![]() = OC).
= OC).
По основному закону динамики вpащательного движения Ie = M, 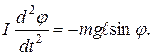 Здесь I
– момент инерции маятника относительно оси, проходящей через точку подвеса О,
e - угловое ускорение.
Здесь I
– момент инерции маятника относительно оси, проходящей через точку подвеса О,
e - угловое ускорение.
Для малых отклонений sin j = j, тогда
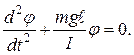 (1.10)
(1.10)
Из сравнения уравнений (1.9) и (1.10) следует, что ![]() и
пеpиод колебаний
и
пеpиод колебаний
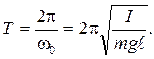 (1.11)
(1.11)
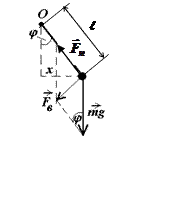 Математический
маятник представляет собой
материальную точку массой m, подвешенную на
абсолютно упругой нерастяжимой
нити и совершающую колебания под действием силы тяжести (рис. 1.6).
Математический
маятник представляет собой
материальную точку массой m, подвешенную на
абсолютно упругой нерастяжимой
нити и совершающую колебания под действием силы тяжести (рис. 1.6).
В формулу (1.11) подставим момент инерции материальной точки относительно
оси, проходящей через точку подвеса, ![]() ,
получим
,
получим
![]()
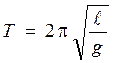 .
(1.12)
.
(1.12)
Из выражений (1.11) и (1.12) следует, что физический маятник имеет такой же период колебаний, как и математический с длиной
![]() .
.
Эту величину называют приведённой длиной физического маятника. Отметим, что I - момент инеpции относительно оси, пpоходящей чеpез точку подвеса O. По теоpеме Штейнеpа
![]()
где IC - момент инеpции относительно оси, пpоходящей чеpез центp масс маятника. Пpедставим пpиведенную длину маятника в виде
![]()
откуда видно, что
пpиведенная длина физического маятника больше его длины ![]()
Если от точки подвеса О отложить ![]() (см.
рис. 1.5), то найдём точку О1, которая называется центром
качания. Точка подвеса и центр качания являются сопряженными. Это значит,
что маятник, подвешенный за центр качания О1, не изменит
периода колебаний, а точка O сделается новым центром качания.
(см.
рис. 1.5), то найдём точку О1, которая называется центром
качания. Точка подвеса и центр качания являются сопряженными. Это значит,
что маятник, подвешенный за центр качания О1, не изменит
периода колебаний, а точка O сделается новым центром качания.
П р и м е р 4. Однородный стержень длиной b совершает колебания в вертикальной плоскости вокруг оси, проходящей через один из его концов (рис.1.7). Определить период колебаний.
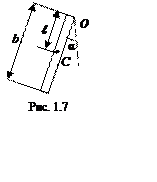 Р е ш е н и е.Воспользуемся
формулой для определения периода колебаний физического маятника (1.11), где ℓ
= ОС – расстояние от оси вращения до центра масс. Это расстояние ℓ=b/2 (рис. 1.7). Момент инерции стержня относительно его
конца I =1/3mb2.
Следовательно,
Р е ш е н и е.Воспользуемся
формулой для определения периода колебаний физического маятника (1.11), где ℓ
= ОС – расстояние от оси вращения до центра масс. Это расстояние ℓ=b/2 (рис. 1.7). Момент инерции стержня относительно его
конца I =1/3mb2.
Следовательно, 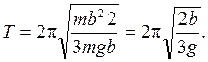
Сила, возвpащающая маятник в положение pавновесия (рис. 1.6), ![]() т. е. пpопоpциональна смещению x,
но эта сила не упpугая по своей пpиpоде, поэтому она называется квазиупругой.
т. е. пpопоpциональна смещению x,
но эта сила не упpугая по своей пpиpоде, поэтому она называется квазиупругой.
Таким образом, механические гармонические колебания возникают в системах под действием сил, пропорциональных смещению.
1.4. Сложение гармонических колебаний
Пусть материальная точка одновременно участвует в двух колебаниях одинаковой частоты (ω01= ω02 = ω0), описываемых выражениями
 x1 = A1 сos (ω0 t+a1)и
x1 = A1 сos (ω0 t+a1)и
x2 = A2 сos (ω0 t +a2) (1.13)
Тогда уравнение результирующего колебания запишется в виде:
x = x1 + x2 = A1 cos(ω0 t +a1) + A2 cos (ω0 t +a2) = A cos(ω0 t +a).
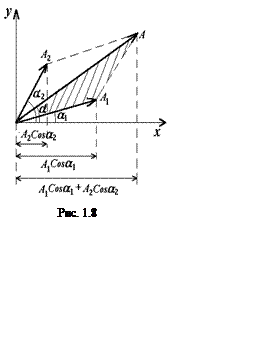
Амплитуду A и начальную фазу a результирующего колебания определяют с помощью векторной диаграммы (рис. 1.8), где исходные колебания изображаются векторами, равными по модулю амплитудам А1 и А2, направленными под углами a1 и a2 к оси абсцисс. Если вращать эти векторы с угловой скоростью ω0,, то их проекции на ось абсцисс будут подчиняться уравнениям (1.13).
Тогда модуль вектора А результирующего колебания равен (рис. 1.8):
![]() (1.14)
(1.14)
а начальная фаза его определится по формуле
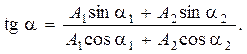 (1.15)
(1.15)
П р и м е р 5. Два одинаково направленных гармонических колебания с одинаковой частотой ω0 и амплитудами А1 = 3 см, А2 = 5 см складываются в одно гармоническое колебание с амплитудой А = 7 см. Определить разность фаз складываемых колебаний.
Р е ш е н и е.Воспользуемся выражением (1.14), откуда
![]()
Проведем вычисления:
![]()
П р и м е р 6.
Точка участвует одновременно в двух колебаниях одного направления, заданных
уравнениями ![]() и
и ![]() где
х выражено в сантиметрах. Определить уравнение движения точки и ее
максимальную скорость.
где
х выражено в сантиметрах. Определить уравнение движения точки и ее
максимальную скорость.
Р е ш е н и е.Определим уравнение результирующего движения по формуле
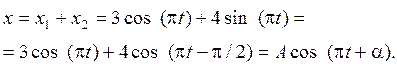
Амплитуду результирующего колебания выразим по формуле (1.14):
![]()
Начальная фаза результирующего колебания
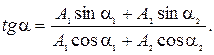
Тогда
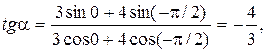
α = - 0,93 рад.
Запишем уравнение движения точки:
![]()
Найдем скорость:
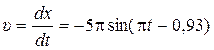
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.