15. Пусть h – высота шарового сегмента,
R – радиус шара, r – радиус
основания шарового сегмента, тогда поверхность шарового сегмента S
вычисляется по формуле ![]() , а объем
шарового сегмента V – по формуле
, а объем
шарового сегмента V – по формуле 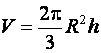 .
.
16. Расстояние между двумя точками d
на плоскости вычисляется по формуле ![]() , где (x1, y1) и (x2, y2) – координаты точек на плоскости.
, где (x1, y1) и (x2, y2) – координаты точек на плоскости.
17. Координаты середины отрезка (x, y) вычисляются по
формулам 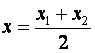 и
и 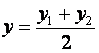 ,
где (x1, y1) и (x2, y2) – координаты начала и конца отрезка.
,
где (x1, y1) и (x2, y2) – координаты начала и конца отрезка.
18. Координаты точки (x, y), которая делит
отрезок в отношении m:n, вычисляются по формулам 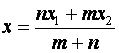 и
и
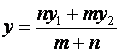 , где (x1, y1) и (x2, y2) – координаты начала и конца отрезка.
, где (x1, y1) и (x2, y2) – координаты начала и конца отрезка.
19. Уравнения прямых в общем виде задаются следующим образом:
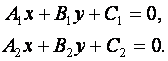
Тогда тангенс угла между двумя прямыми вычисляется по формуле
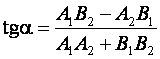 ,
, ![]() .
.
20. Пусть h – высота трапеции, a
и b – ее основания, тогда площадь трапеции S
вычисляется по формуле 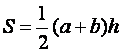 , а средняя линия
lср – по
формуле
, а средняя линия
lср – по
формуле 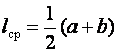 .
.
21. Пусть а – сторона равностороннего треугольника, тогда его
площадь S вычисляется по формуле 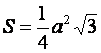 .
.
22. Пусть h – ширина кольца, R
и r – внешний и внутренний радиусы, тогда площадь кольца S
вычисляется по формуле ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.