Кристалл как идеальный газ квазичастиц

Кристалл как идеальный газ квазичастиц

1. Связанные осцилляторы. Фононы.

Классический подход.Отдельная частица, даже если она движется под действием консервативных, гироскопических и диссипативных сил, представляет собой, конечно, самую простую физическую систему. На практике весьма часто приходится сталкиваться с частицами, которые взаимодействуют друг с другом. Примером могут служить атомы в молекуле, ионы в кристалле, нуклоны в ядре. Попытки описать теоретически свойства таких многочастичных систем даже на классическом (неквантовом) уровне наталкиваются на значительные трудности. Рассмотрим один из способов обхода этих трудностей на примере двух связанных пружинных маятников.

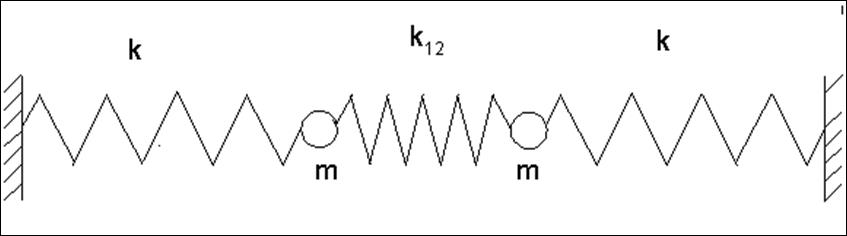
Рис. 1. Связанные пружинные маятники. Грузики могут двигаться только вдоль горизонтальной прямой.

Пусть  и  -- горизонтальные смещения грузиков от положений равновесия. Система консервативна, её уравнения движения имеют вид

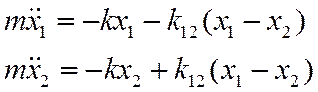                                                        (1)

Решение этой системы дифференциальных уравнений сильно упрощается, если ввести новые обобщённые координаты  и . Уравнения для новых координат ничем не отличаются от уравнений для независимых осцилляторов

                                  (2)

Итак, систему двух связанных осцилляторов можно анализировать как систему двух независимых осцилляторов, каждый из которых колеблется с одной собственной частотой (как говорят, совершает нормальное колебание).

Каждое нормальное колебание отвечает определённой симметрии движения системы – моде колебаний. Для рис.2 есть жёсткая мода (движение грузиков навстречу друг другу из положения равновесия, когда крайние пружинки одинаково растягиваются, а средняя сжимается; жёсткость этой моды ) и мягкая мода (движение грузиков в одном направлении из положения равновесия, когда одна из крайних пружинок растягивается, другая на столько же сжимается, а средняя остаётся недеформированной; жёсткость этой моды ).

В общем случае система из  связанных одномерных осцилляторов будет иметь  собственных частот. Любое произвольное колебание этой системы есть суперпозиция нормальных колебаний (принцип суперпозиции справедлив для всех линейных систем). Самая мягкая мода отвечает движению всех грузиков в одну сторону – она является самой коллективизированной и возбуждается в первую очередь. Частота этой моды очень мала и определяется размерами кристалла. Самая высокая частота определяется размерами элементарной ячейки.

В случае кристалла ситуация похожа, только колебания, конечно, трёхмерные. В результате тепловые колебания кристаллической решетки и распространения звука в ней можно представить как суперпозицию нормальных колебаний фиктивных независимых осцилляторов, которые, однако, не локализованы.

Квантовый подход. Мы уже знаем, что энергия любой системы, совершающей финитное движение, квантуется. В соответствии с проанализированным выше классическим результатом, энергию  связанных осцилляторов можно представить как сумму энергий  независимых осцилляторов. Для каждого из осцилляторов энергия квантуется по закону

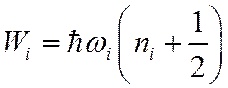.                                                          (3)

Таким образом, задача о  взаимодействующих частицах оказывается полностью сведена к движению 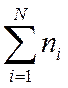 независимых «как бы» частиц звука (для них используется термин «квазичастица»), которые называются фононами. О движении, соответствующем одной собственной частоте , говорят как о движении данной моды (данного типа). Если, например, , говорят, что в 3-й моде имеется 5 фононов.

Использование квазичастиц колебаний кристаллической решётки – фононов – позволяет заменить систему, состоящую из огромного числа взаимодействующих атомов кристаллической решётки на идеальный газ фононов, а с идеальным газом – невзаимодействующими (иди редко и слабо взаимодействующими квазичастицами) работать намного легче.

Фононы ответственны за тепловые свойства кристалла и распространение в нём звука. Чем жёстче кристалл, тем быстрее распространяются в нём фононы. Вот почему у кремния и алмаза теплопроводность такая большая, а у свинца такая маленькая.

2. Электроны проводимости и дырки.

До сих пор мы полностью игнорировали тот факт, что в любом кристалле некоторая часть атомов ионизована. Если эта часть заметна, кристалл относят к полупроводникам. Типичные зонные диаграммы полупроводников изображены на рис.2.

nПП

рПП

iПП

Рис.2  Типичные зонные диаграммы электронного (nПП, донорная примесь ), дырочного (рПП, акцепторная примесь) и собственного (без примесей) полупроводников.

Чёрные кружочки в валентной зоне – электроны, которые связаны в атомах, они не являются носителями электрического тока. Чёрные кружочки в зоне проводимости – электроны проводимости, это квазичастицы – возбуждённые состояния полупроводника. Светлые кружочки в зоне проводимости – дырки, они являются носителями электрического тока, это квазичастицы – возбуждённые состояния полупроводника. Зону проводимости можно считать почти заполненной светлыми кружочками, которые, однако, не отвечают ничему реальному: они не являются носителями электрического тока.

При данной температуре между электронами проводимости и дырками устанавливается термодинамическое равновесие. Это значит, что скорость генерации равна скорости рекомбинации. Следить за одним конкретным электроном, оторвавшимся от атома, бессмысленно: важно только, что есть определённое количество электронов проводимости .