где m – масса зеркала, h – постоянная Планка. В работе [5] приводятся пример измерения l таким способом в интервале от 4 × 10-18 м до 10-7 м. Установка достаточно сложна как идейно, так и конструктивно. Для контроля перемещения используется измерение частоты биений трех лазеров – двух измерительных и одного эталонного. Следует обратить внимание, что для пассивного интерферометра порог чувствительности к перемещениям гораздо хуже и составляет 10-13 ¸ 10-14 м при базе (расстоянии между зеркалами) порядка 1 м. Ограничение связано с шумами и минимальной энергией детектирования.
В случае газообразных, жидких сред и плазмы объекты (атомы, молекулы, частицы) постоянно находятся в движении. Поэтому расстояния измеряются косвенными методами – из количества частиц, объёма среды, давления среды на стенку и т. д. Расстояние, которое в нормальных условиях пробегает молекула воздуха до столкновения с другой молекулой воздуха lпр ~ 10-7 м примерно в 100 раз больше среднего расстояния между молекулами lатм ~ 10-9 м. Длина свободного пробега электронов в металле определяется количеством кристаллических дефектов и составляет lэл ~ 10-8 м.
Некоторые расстояния, такие как разницы длин волн в спектроскопических измерениях, носят условный характер и их не стоит отождествлять с размерами конкретных физических объектов.
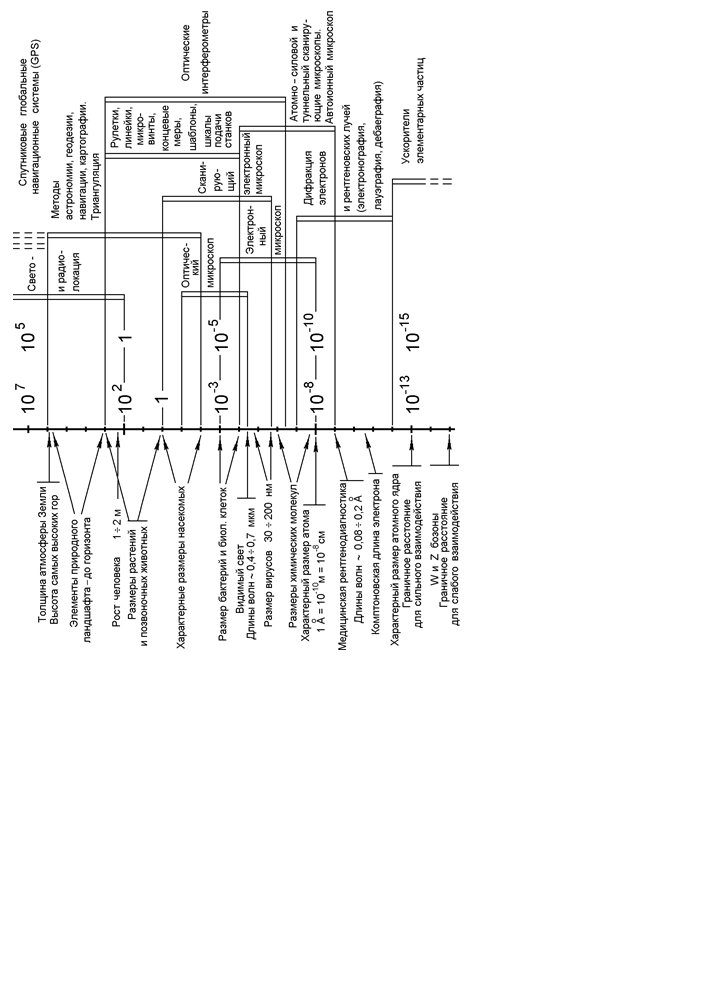
Для дистанций от 0,1 мм до сотен километров имеется ряд методов, основанных на использовании триангуляции и оптических приборов с точными угловыми и линейными шкалами – теодолитов, секстанов, катетометров, гониометров. Эти методы используются для геодезии, картографии, навигации и астрономии, при точном монтаже крупных технических объектов (таких, как самолёты, корабли, мосты, тоннели и т. д.). Триангуляцией называется нахождение длины одной из сторон треугольника, когда известны три других параметра того же треугольника, среди которых обязательно должна быть длина. При этом форма треугольника и углы выбираются таким образом, чтобы эту длину можно было измерить непосредственно эталонной мерой – линейкой, рулеткой или микровинтом, либо сравнить с размерами точно измеренного подобного треугольника. Процесс аэрофотосъемки и фотосъемки из космоса является также разновидностью триангуляционного метода. Методы радио- и оптической локации применяются для расстояний от 1 м до межпланетных. Законы небесной механики и астронавигации позволяют очень точно измерять расстояния между объектами в пределах Солнечной системы и даже делать оценки расстояний для гораздо более крупных объектов. Как мы увидим в следующих лекциях, точность астрономических измерений в первую очередь зависит от точности измерений времени.
Показанные на шкале пределы расстояний являются характерными – такими, какие чаще всего используются в повседневной практике. Многие пределы могут быть расширены, как это показано пунктиром для законов небесной механики и методов навигации и картографии. Широко применяемые в настоящее время спутниковые глобальные навигационные системы (GPS) являются синтезом астронавигации, радиолокации и геодезии. Они позволяют измерять расстояния в интервале от 1 м до размеров Земли. Область радиолокационных измерений может быть расширена за счёт активной ретрансляции сигнала. Это обычно происходит при посылке межпланетных зондов. В сторону меньших размеров известны случаи применения оптической локации для измерения размеров объектов ~ 30 мкм. Данные параметры достигнуты при оптической когерентной локации фемтосекундными импульсами света, когда различаются отдельные слои клеток биологических тканей.
Чтобы не усложнять восприятие, некоторые методы не отражены на шкале. Например, акустическая локация должна занять интервал от 10-3 до 104 м. Интервал может быть расширен до размеров Земли, если включить в него методики сейсмического зондирования.
Следует отметить, что для областей активной повседневной и технологической деятельности человека в интервале от 10-10 м до 107 м число независимых методик для измерения расстояния больше, чем для остальных участков шкалы. На границах шкалы количество методов измерения уменьшается. При этом, как правило, применяются непрямые, косвенные методы – эффект Доплера и некая модель Вселенной, подсчёт координат, направлений и количества вылетевших элементарных частиц и т. д.
В шкале расстояний есть провал в четыре порядка. Начиная с орбиты Плутона (половина длины главной полуоси орбиты 5,9 × 1012 м) и вплоть до ближайшей звезды Проксимы Центавра (4,3 световых лет » 4×1016 м), люди пока не могут регистрировать никаких объектов. Известно, что там есть кометы, но они не доступны для наблюдения. Облако комет формально может простираться до дистанции 50000 а. е. ~ 1 св. года. Как показывают оценки, предел влияния гравитационного поля Солнца примерно равен 1/3 от расстояния до ближайшей звезды.
Расстояния до ближайших звезд измеряются методом триангуляции по параллаксу – смещению положения звезды относительно удаленных звезд при движении Земли по орбите. Это нашло отражение в названии внесистемной астрономической единицы длины – параллакс-секунде (парсек). Парсек – это расстояние на котором диаметр земной орбиты виден под углом 1 секунда:
1 парсек = 3,26 световых лет = 3,086 × 1016 м;
1 св. год = 0,31 парсек = 0,9461 × 1016 м.

Метод параллакса годится для расстояний от 1 до 100 парсек – для более удаленных звезд параллакс столь мал, что он меньше ошибок измерения углового положения звезд на небе оптическими методами.
Знание среднего размера для различных классов галактик дает возможность оценки расстояний до них по угловому размеру. Этот метод накрывает дистанции от 90 кпк до 10 Мпк.
При наблюдении удалённых галактик, на больших угловых увеличениях количество галлактик превышает количество звезд, видимых на небе, а угловой размер является слишком малым для триангуляционных измерений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.