Плазма. Квазинейтральность. Дебаевское экранирование, страница 2

Управляемый термоядерный синтез (УТС). Пожалуй, УТС является наиболее многообе­щающим приложением физики плазмы. Поясним, что под неуправляемым синтезом подразу­мевают взрыв водородной бомбы. Уже во время работы над водородной бомбой возникла идея об использовании реакции термоядерного синтеза в энергетике. В настоящее время удалось достичь таких параметров плазмы (плотности и температуры), при которых энерговыделение в реакции синтеза лишь в 2-4 раза ниже мощности, затрачиваемой на нагрев плазмы; фактиче­ски, остался всего один шаг до полностью самоподдерживающейся реакции УТС. Тем не менее, экономически конкурентоспособные термоядерные электростанции пока остаются делом отда­ленного будущего. Уже ясно, что эта предполагаемая отрасль энергетики потребует огромных начальных вложений — порядка сотен миллиардов долларов. Существуют и области примене­ния УТС на уже достигнутом уровне энерговыделения. Плазма, в которой идет термоядерная реакция синтеза, является мощным источником нейтронов.

Плазменная электроника. Разнообразные колебательные и волновые процессы могут быть использованы для полу­чения и преобразования электромагнитных волн и сигналов в электрических цепях. Давно известны такие источники СВЧ-излучения, как клистроны и магнетроны, в которых исполь­зуется заряженная (электронная) плазма; в будущем можно ожидать появления устройств для преобразования частот на основе плазменных сред. При определенных условиях в плазме могут развиваться колебания электрического поля с очень высокой амплитудой, в том числе с такой, какая не может быть достигнута традиционным способом (скажем, в вакуумном зазоре между двумя проводниками под разным потенциалом). Дело в том, что поле с напряженностью от 1 МВ/см буквально вырывает электроны из металла, в результате развивается так называемый вакуумный пробой. В плазме, вдали от проводников, никаких принципиальных ограничений на величину поля не существует. Примером области, в которой может быть использовано это свойство плазмы, являются ускорители элементарных частиц. Здесь увеличение ускоряющего поля приведет к увеличению энергии частиц при том же радиусе кольца.

2  Квазинейтральность. Дебаевское экранирование

Ранее уже отмечалось, что плазма, хоть и состоит из заряженных частиц, в среднем обычно является нейтральной. Такое свойство плазмы получило название квазинейтральности. Уточ­ним его следующим образом: квазинейтральность — это малость суммарной плотности заряда по сравнению с плотностью заряда, создаваемой зарядами одного знака (скажем, электронами). На малых масштабах расстояний квазинейтральность отсутствует: так, если мы рассмотрим область с объемом, равным 1/п_е, то в среднем в нем находится одна заряженная частица, положительная или отрицательная. Оценим максимальный масштаб расстояния, на котором возможно значительное отклонение от квазинейтральности. Рассмотрим среду, в которой при­сутствуют положительно и отрицательно заряженные частицы с зарядами q = ±е и концентра­циями n+ = п_- = п. Представим, что в результате флуктуации теплового движения частиц в шарообразной области радиуса r₀остались заряды только одного знака (скажем, ионы). Эта область будет иметь заряд q = , и иметь потенциал

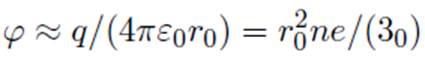
Такая область может возникнуть, если средняя кинетическая энергия электронов будет превы­шать величину потенциального барьера:

Отсюда получаем условие для размера области:

здесь мы ввели обозначение г_кв — радиуса квазинейтральности. Если же размер области много больше г_кв, существенного отклонения от квазинейтральности в ней возникнуть не может. Итак, ионизованный газ можно считать квазинейтральным, если характерный размер области, занятой им, много больше радиуса квазинейтральности.

Рассмотрим вопрос о характерном времени, в течение которого устанавливается квазиней­тральность. Процесс установления выглядит следующим образом: если в некоторой области образовался избыток заряда, например, положительного знака, то возникает электрическое по­ле, направленное из этой области, выталкивающее положительные заряды и притягивающие отрицательные. Этот процесс можно описать следующим образом. Пусть до возникновения возмущения частицы покоятся. В движение приходят в первую очередь электроны, как бо­лее легкие. Введем время свободного пробега электрона т. Потерю направленного импульса электрона за время т можно описать действием силы трения, равной

Запишем уравнение движения электрона под действием электрического поля и силы трения:

Ток электронов выражается через скорость как ^ = — еп_еи, поэтому, если считать, что кон­центрация электронов меняется слабо (п_е ~ сопзт), из уравнения движения электрона можно

получить уравнение для тока:

Беря от обеих частей уравнения дивергенцию и используя уравнения Максвелла

получаем уравнение плотности заряда в данной точке:

В это уравнение входит величина

являющаяся квадратом так называемой плазменной

частоты шр (другое название — ленгмюровская частота). Вид этого уравнения знаком из теории затухающих колебаний: колеблющейся величиной является р_ег, собственной частотой является

шр, коэффициентом затухания

. В случае, когда затухание мало, т.е. плазменная часто-

та много больше частоты столкновений, заряд колеблется с частотой, близкой к плазменной. Такие колебания известны как ленгмюровские или продольные электростатические колебания (или волны). Затухают эти колебания за время 2т. В противоположном случае, когда частота столкновений превышает ленгмюровскую, колебаний не происходит и заряд экспоненциально

падает за обратное время

Последнее выражение, как легко

убедиться, равно электропроводности плазмы в постоянном электрическом поле, умноженной на 4п.

Примером стремления плазмы к квазинейтральности является экранирование электриче­ского поля заряда или проводника, помещенного в плазму. Определим, какое поле создает точечный заряд в плазме с учетом влияния заряженных частиц плазмы. Задача обладает сфе­рической симметрией, поэтому потенциал будет зависеть только от расстояния до заряда, <р(г).

Уравнение Пуассона

в этом случае будет выглядеть следующим образом:

Распределения плотностей электронов и ионов можно найти из предположения термодинамиче­ского равновесия в плазме, когда справедливо распределение Больцмана:

Определим потенциал на больших расстояниях от заряда, где

В этих условиях мы

можем воспользоваться разложением экспоненты

и уравнение на потенциал будет

таким: