Проектирование, виды проектирования в зависимости от степени автоматизации. Проектирование телекоммуникационных сетей на ЭВМ

1.  Проектирование, виды проектирования в зависимости от степени автоматизации. Проектирование телекоммуникационных сетей на ЭВМ.

Проектирование – создание подробного описания, которое необходимо для реализации технического объекта в заданных условиях.

Проектирование может быть трех типов:

1.  Неавтоматизированное (ручное) – проектирование без применения ЭВМ.

2.  Автоматизированное – проектирование с применением ЭВМ и при непосредственном участии человека.

3.  Автоматическое – выполняет только ЭВМ без участия человека.

Исходным этапом для любого типа проектирования является этап проектно-изыскательных работ на местности.

Техническая база для автоматизации этапа проектно-изыскательских работ (робототехнические комплексы, многофункционального автомата) имеется, но из-за дороговизны реализации такого подхода в настоящее время нас в стране этап проектно-изыскательских работ выполняется, как правило, человеком. Поэтому любое проектирование, даже с высокой степенью автоматизации будет автоматизированным, но не автоматическим.

Проектное решение – описание объекта проектирования в промежуточном или окончательном виде, которое необходимо и достаточно для рассмотрения и определения дальнейшего направления проектирования или полного окончания проектирования.

Результат проектирования – оформленное проектное решение, которое удовлетворяет всем необходимым требованиям, для того чтобы объект был реализован.

Проектная процедура – формализованная программа действий, при выполнении которых мы получаем проектное решение.

Проектная операция – часть проектноц процедуры, алгоритм которой неизменен для целого ряда проектных процедур.

Унифицированная проектная операция – это такая проектная операция, у которой алгоритм не зависит от объекта проектирования, то есть можно применять её в разных отраслях (например, составление таблиц для склада).

Для того, чтобы выполнить проектирование на ЭВМ, очень важно выбрать тип моделирования:

1.  Натурное

2.  Математическое

3.  Имитационное

Для работы с ЭВМ надо математическое моделирование. Наши модели - это модели в виде графов, реализует математическое моделирование, и дают возможность ввести в ЭВМ всю информацию о телекоммуникационной сети.

2.  Основные виды матриц графовых моделей телекоммуникационных сетей.

Матрица расстояний – квадратная матрица D, состоящая из элемента {d_ij}, где d_ij равна расстоянию r от вершины x_i до вершины x_j в графовой модели сети, причем если x_j не достигла из вершины x_i, то считают что r (x_i, x_j)=¥.

В матрицы расстояния присутствует нулевая диагональ, она является отражением первой аксиомой Фреше. Матрица расстояний симметрична относительно нулевой диагонали – это отражение второй аксиомы.

Экцентриситет вершины x (e(x)) – это длина максимального из расстояний от данной вершины до других вершин графа (иначе расстояние от данной вершины до наиболее удаленной вершины графа). e(x)=max r(x, y_i), yÎX.

Максимальный из эксцентриситетов в графовой модели называется диаметром. d(G)=max e(x_i)

Минимальный из эксцентриситетов в графовой модели называется радиусом. r(G)=min e(x_i)

Вершины (одна или несколько), в которой достигаются значения радиуса называются центральными вершинами (или просто центрами).

Вершины, в которых эксцентриситет достигает значение диаметра называются периферийными.

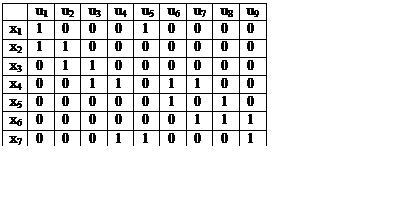 Матрица инцидентности – это прямоугольная матрица М, состоящая из элементов {m_ij}, в которой m_ij – элемент равен 1,тогда и только тогда, когда вершина x_i инцидентна ребру u_j, и элемент матрицы m_ij =0 в противном случае. Формат матрицы

 Матрица смежности(вершин) (матрица соседства, матрица смежности графа) графа G – это матрица квадратного типа А, состоящая из элементов {а_ij}, причем а_ij=1, тогда и только тогда, когда вершина графа x_i смежна с вершиной x_j, и a_ij=0 в противном случае.

3.  Метрические характеристики графовых моделей и аксиомы Фреше.

Маршрут в графе,модел.тк сеть-это чередующаяся послед-ть вида х1,u1,x2,u2..Uk-1,uk,в которой любая пара двух соседних элементов инцидентна.

Цепь-в граф.модели-это маршрут,в котором все ребра различны.

Простая цепь-в которой все вершины различны

                                         Метрические характеристики

Расстояние  r-расстояние между парами вершин Хи Y,наз.длина кратчайшей(или минимальной)(х,y)цепи.

r(х,y)наз.x,y, y принадлежит Х.

Введенные т.о.поняти расстояния удовл-т 3 аксиомам Фреше

1.Аксиома рефлексивности(замкнутость объекта самого на себя)(х,х)=0

2.Аксиома симметричности (х,у)= r(у,х)

3.Аксиома транзитивности хЕ Х,уЕХ,zЕХ, r(х,у) +r(у,z) >=r(x,z)

Правило треугольника  

 

                                            х

4.  Алгоритм Прима-Краскала и его применение.

Основная постановка задачи: на практике часто встречается задача о нахождении кратчайшего пути телекоммуникационной сети. Пусть на некоторой территории размещены пункты, которые необходимо связать коммутационной сетью минимальной стоимости. Пусть в результате предварительных изысканий определены всевозможные трассы для прокладки коммуникаций и оценена стоимость реализации каждой трассы. Если сопоставить каждому пункту вершину графа, то 2 вершины будут инцидентны ребру. Если на практике пункты должны быть соединены конкретной трассе, этому ребру можно задать вес соответствующей стоимости реализации данного участка трассы. Неоходимо найти такую оптимальную структуру коммутационной сети, которая будет соответствовать минимальному или кратчайшему остову во взвешенном графе, то есть требуется найти кратчайшие остовое дерево, имеющего минимальный суммарный вес ребер.

Первая разновидность алгоритма Прима-Краскала.

Шаг 1: упорядочить все ребра исходного графа G по убываю их весов (то есть построить некоторой численный ряд);

Шаг 2: рассмотреть последовательно каждое ребро в построенном ряду, начиная с ребра наибольшего веса и определить можно, ли удалить это ребро из графа, не нарушив его связности (то есть определить, есть ли еще какой то путь, не считая пути через удаляемое ребро, по которому можно пройти от 1 до 2 вершины данного ребра). Оставшиеся ребра будут образовывать остовное дерево графа с минимальным суммарным весом (он подсчитывается как сумма весов всех ребер, которые вошли в дерево). Пример: дана сеть поселка, которую нужно радиофицировать. Сеть представлена в виде графа, вершины которого обозначены номерами и соответствуют отдельным поселкам. Ребра графа имеют веса по стоимости работ по радиофикации на отдельных участках. Найти вариант радиофикации сети поселка с минимальной стоимости работ.

Вторая разновидность алгоритма Прима-Краскала.

Шаг 1: упорядочить все ребра по возрастанию весов (составляем численный ряд)

Шаг 2: первое в ряду ребро включается в будущее дерево обязательно. В соответствии с числовым рядом последовательно решается вопрос, включить ли в будущее дерево новое ребро (если при таком включении может образоваться цикл с уже включенными в дерево ребрами, то повторно ребро в дерево отключать нельзя). Полученное остовное дерево имеет минимальный суммарный вес ребра. Пример: условия задачи аналогично предыдущем.

Третья разновидность алгоритма Прима-Краскала. (для многопроцессорных вычислительных машин).

Шаг 1: каждый процессор «выхватывает» из предложенного графа один цикл  и выбрасывает из этого цикла ребро с наибольшим весом , если таких ребер несколько , то выбрасывает только одно. Оставшиеся ребра образуют остовное дерево минимального суммарного веса.