Определение прочностных и деформативных характеристик грунтов. Составление сочетаний нагрузок и выбор их для расчета. Расчет фундамента на естественном основании, страница 2

Краевые давления под подошвой фундамента Р_max, Р_min находят в предположении линейного распределения давления по грунту в направлении действия момента по формуле

,

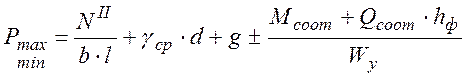где h_ф – высота фундамента; W_y – момент сопротивления подошвы фундамента относительно оси y.

;

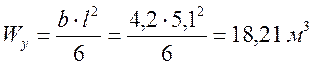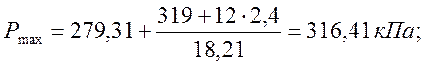
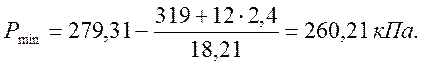
Проверяем чтобы средняя величина давления по подошве была меньше расчетного сопротивления, и удовлетворялось условие для краевых ординат давлений:

а)  ,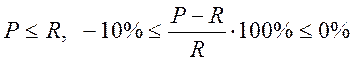

;

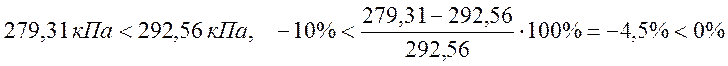б)  ;

в)  .

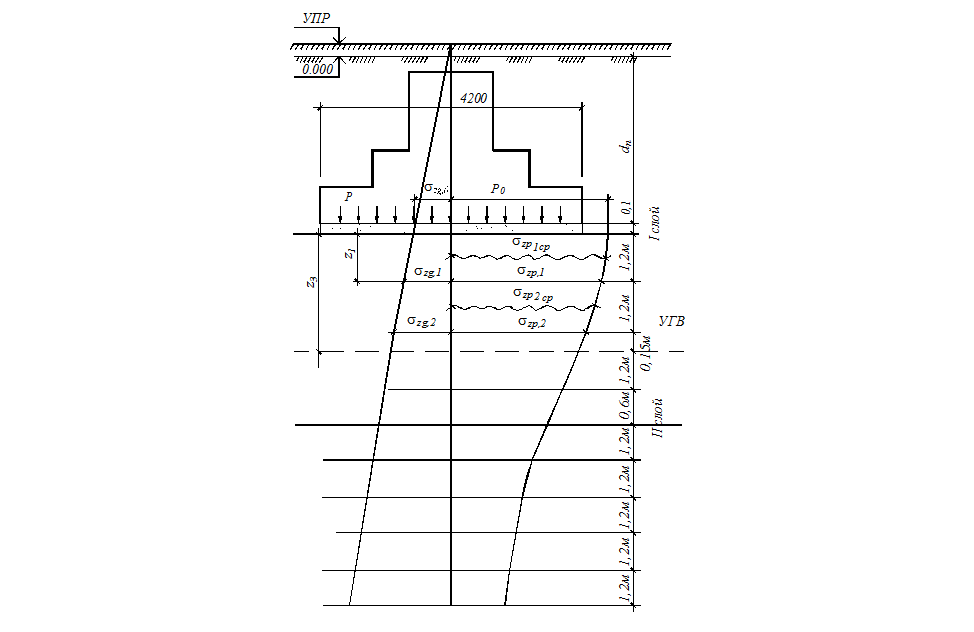
Для окончательного принятых размеров фундамента определяем абсолютную осадку методом послойного элементарного суммирования.

2.3.  Расчет осадок фундаментов методом послойного

 элементарного суммирования

Схема для расчета абсолютной осадки фундамента приведена на рис.2.3.1.

Рис. 2.3.1.  Схема для расчета абсолютной осадки фундамента

Рис.2.3.1. Схема осадки фундамента

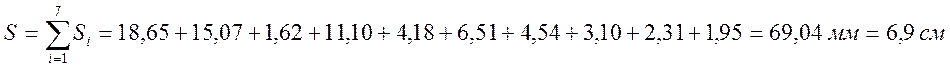
Таблица 2.3.1

Напряжения в горизонтальных сечениях в грунте ниже подошвы фундамента

Наименование грунта	, кН/м3	, м	МПа			, МПа	, МПа	, МПа	, мм
Песок пылеватый, средней плотности, насыщенный водой	19	2,65	50,35	10,07	1,000	228,96	213,73 172,64 148,14 127,19 95,82 73,27 51,06 34,92 25,99 21,98	11,0	18,65 15,07 1,62 11,10 4,18 6,51 4,54 3,10 2,31 1,95
	19	1,20	73,15	14,63	0,867	198,51		11,0
	19	1,20	95,95	19,19	0,641	146,76		11,0
	19	0,15	98,80	19,76	0,653	149,51		11,0
	9	1,20	109,60	21,92	0,458	104,86		11,0
	9	0,60	115,00	23,00	0,379	86,78		11,0
Глина пластичная	9,6	1,20	126,52	25,30	0,261	59,76		10,8
	9,6	1,20	138,04	27,61	0,185	42,36		10,8
	9,6	1,20	149,56	29,91	0,120	27,48		10,8
	9,6	1,20	161,08	32,22	0,107	24,50		10,8
	9,6	1,20	172,60	34,52	0,085	19,46		10,8

Значение конечной осадки фундамента не превышает допустимого значения.

2.4.  Расчет затухания осадки фундамента во времени

Найдём высоту эквивалентной эпюры уплотняю их давлений:

,

где  - коэффициент эквивалентного слоя, принимаемый равным при μ=0,3.

Вычерчиваем эпюру уплотняющих давлений (рис. 2.4.1) и выписываем из задания значения коэффициентов пористости, сжимаемости и фильтрации для глинистого слоя.

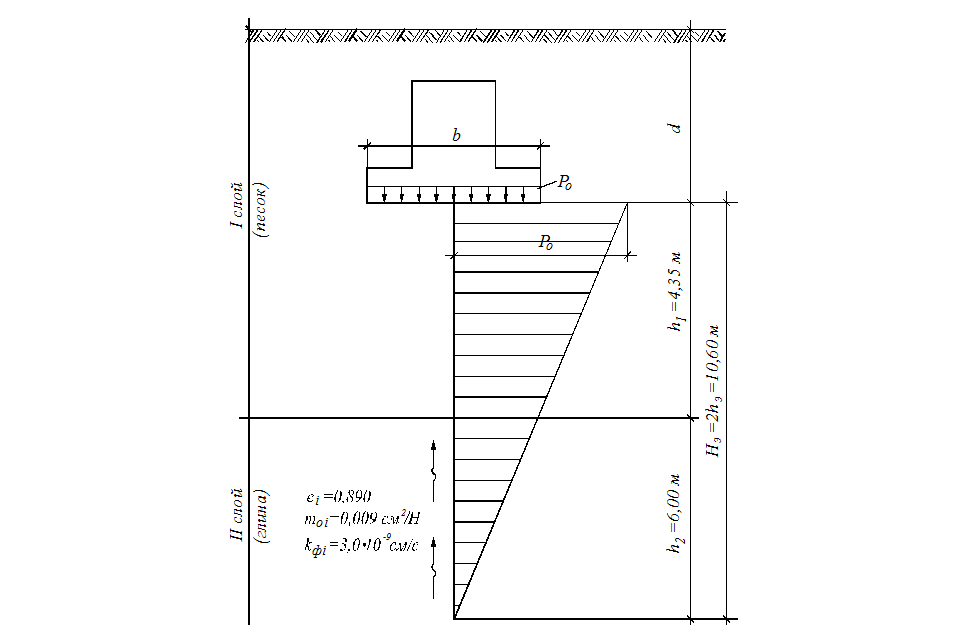
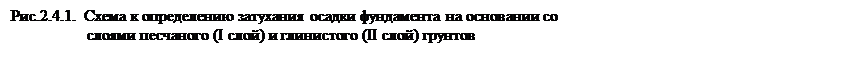Определяем коэффициент относительной сжимаемости глинистого слоя:

,

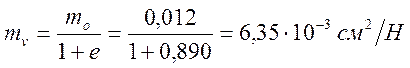где m_о– коэффициент сжимаемости слоя.

Найдём коэффициент консолидации глинистого слоя:

.

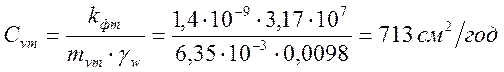Вычислим затухание осадки во времени в табличной форме (табл. 2.4.1).

                                                                                                                   Таблица 2.4.1

Затухание осадки во времени

U (2)	N	, год	, см
0,05 0,20 0,40 0,70 0,98	0,002 0,02 0,13 0,69 3,49	0,41 4,10 26,3 141,34 714,89	0,345 1,380 2,760 4,830 6,762

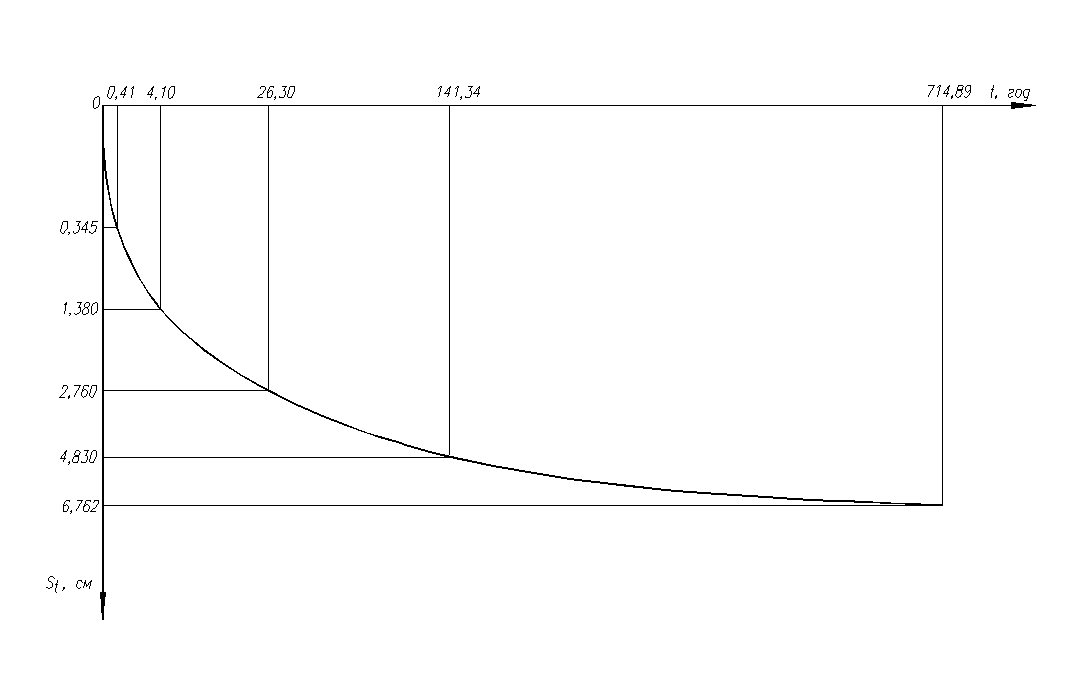
Строим график затухания осадки во времени (рис. 2.4.2) с помощью таблицы, составленной выше.

рис. 2.4.2.   график затухания осадки во времени

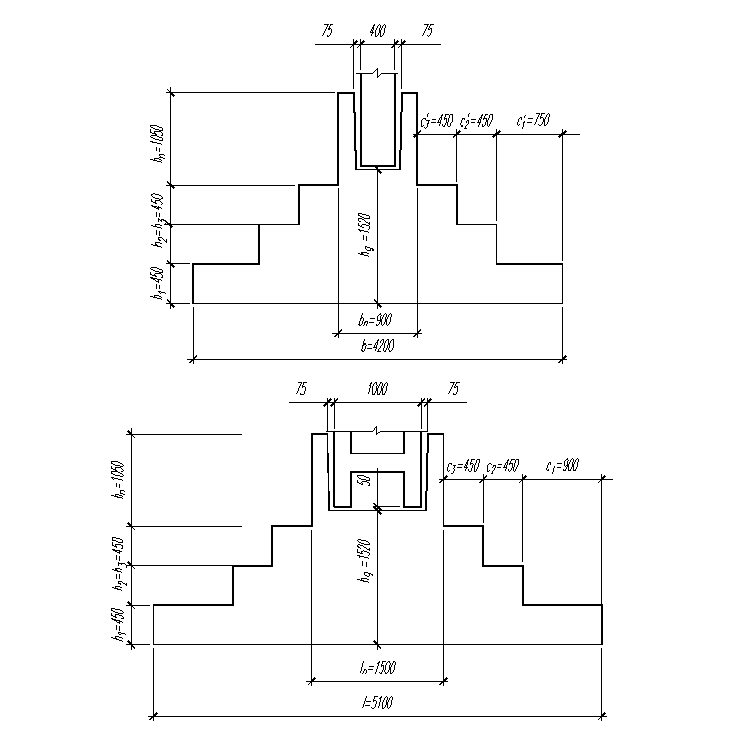
2.5.  Конструирование фундамента

Общая высота фундамента .

Размеры подколонника в плоскости действия изгибающего момента:

,

где  h_к – больший размер прямоугольного сечения колонны, м;

0,075 – минимальный зазор между стенкой стакана и колонной, м;

d_с – минимальная толщина стенки стакана в плоскости изгибающего момента;

.

Размеры подколонника из плоскости изгибающего момента:

,

где b_к – меньший размер сечения колонны, м;

0,175 – минимальная толщина стенки стакана из плоскости изгибающего момента, м.

Вынос плитной части фундамента относительно граней подколонника:

а) в плоскости изгибающего момента

;

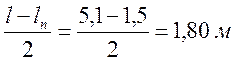б) из плоскости изгибающего момента

.

Принимаем бетон класса В15, ,  (рис.2.5.1).

Рис. 2.5.1. Размеры ступеней трехступенчатого фундамента

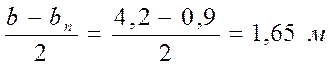2.6.  Расчёт фундамента по прочности

2.6.1.  Расчёт фундамента на продавливание

Расчётные усилия:

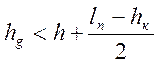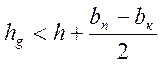Устанавливаем схему образования пирамиды продавливания с помощью соотношений :  и , где ; ; ; ; ; .

; .

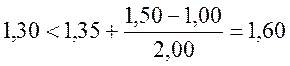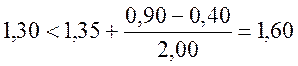Так как данные условия выполняются, то пирамида продавливания образуется от дна стакана.

Схема определения продавливающей силы показана на рис. 2.6.1.

; .

;

.

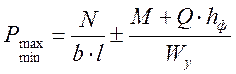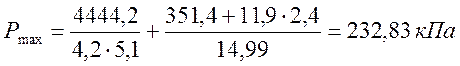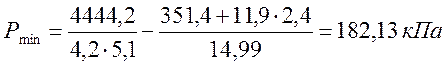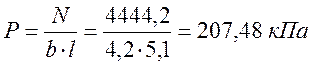
Расчёт на продавливание при образовании пирамиды от дна стакана производим:

– в плоскости действия изгибающего момента из условия:

,

где  N  – расчетная продавливающая сила;

P  – максимальное давление под подошвой фундамента;

А_о – площадь прямоугольника ABCD;

 – коэффициент, принимаемый равным для тяжелых и ячеистых бетонов 1;

b_ср – размер меньшей стороны дна стакана;

R_bt – расчетное сопротивление бетона осевому растяжению при , ;

– рабочая высота дна стакана, принимаемая от дна стакана до плоскости расположения растянутой арматуры, .

;

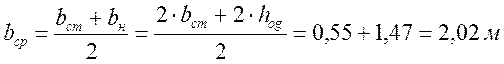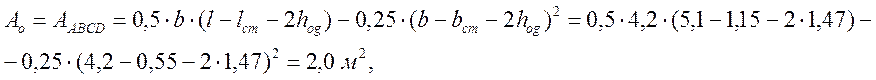
тогда , условие выполняется.

– из плоскости действия изгибающего момента из условия:

,

;

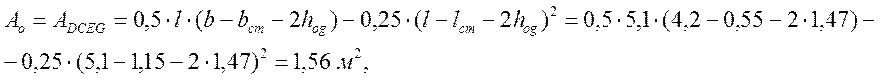тогда , условие выполняется.

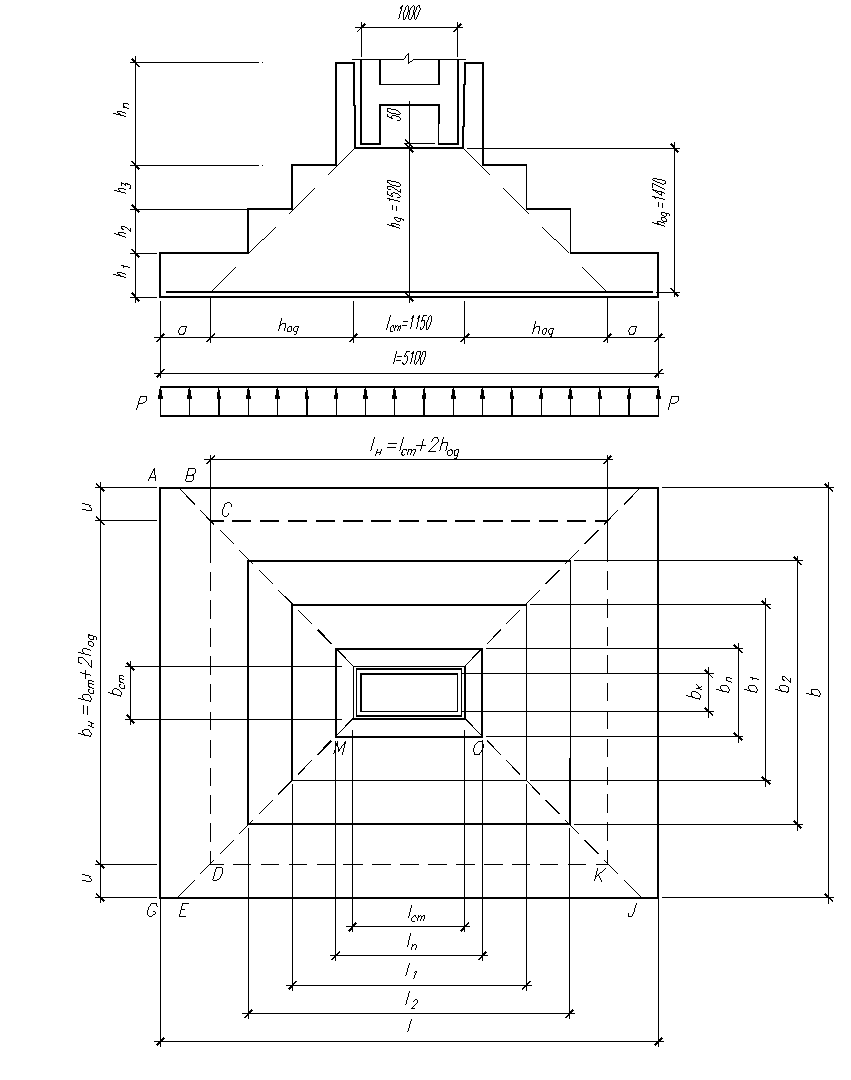
Рис. 2.6.1. Схема определения продавливающей силы

2.6.2. Проверка первой ступени по поперечной силе

а)  в плоскости действия момента:

,

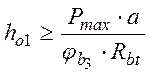где  – коэффициент, принимаемый равным 0,6 для тяжелого бетона.

.

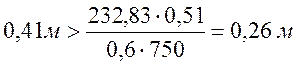 – условие выполняется.

б)  из плоскости изгибающего момента:

,

,

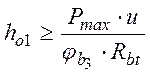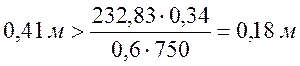 – условие выполняется.

2.6.3.  Расчёт фундамента на изгиб

Вычерчиваем размеры фундамента с соответствующими эпюрами реактивного давления грунта в плоскости и из плоскости изгибающего момента. Величины Р_max, P_min и P принимаем из расчета по I гр. п.с.