Нелинейно-оптические процессы в доменных структурах тетрабората стронция, страница 2

Экспериментальное исследование этой зависимости выполнено при использовании излучения накачки на длине волны 532 нм для процесса генерации второй гармоники этого излучения с длиной волны 266 нм. Теоретическая и экспериментальная угловая зависимость сигнала на удвоенной частоте при повороте кристалла вокруг оси, совпадающей с направлением поляризации накачки, представлена на рисунке 3. Данная зависимость хорошо согласуется с результатами теоретических расчетов по формуле (2) в диапазоне углов поворота от -15 до 15 градусов. Первоначально для построения теоретической кривой использовалось расчетное значение волновой растройки, полученное с использованием показателей преломления, вычисленных по формуле Зельмайера, с коэффициентами [9]. При этом согласие расчетной зависимости с экспериментом оказалось невысоким. Расчетная кривая очень чувствительна к изменению величины . В связи с этим для сопоставления экспериментальных и расчетных данных использовался метод наименьших квадратов. В качестве варьируемой величины была взята волновая растройка, поскольку точность её определения определяется точностью аппроксимации показателей преломления. Наилучшее согласие наблюдается при . Для определения фактора увеличения эффективности генерации второй гармоники за счет случайного квазисинхронизма в качестве образца сравнения использовался монодоменный образец толщиной 432 мкм. Фактор увеличения эффективности генерации второй гармоники при случайном квазисинхронизме в нерегулярной доменной структуре, соответствующей углу поворота 10 градусов, составил 501 раз по отношению к эффективности генерации второй гармоники в монодоменном образце, взятой при нормальном падении излучения. Экспериментальное значение данного фактора практически совпадает с расчетным, равным 500.

Наибольший практический интерес представляет ГВГ излучения ближнего УФ диапазона, в частности, излучения на длине волны 354.7 нм, поскольку ВГ этого излучения попадает в полосы интенсивного поглощения большинства известных нелинейных кристаллов, кроме SBO. На рисунке 4 приведен результат расчета эффективности ГВГ вблизи указанной длины волны. Расчеты показывают, что для достижения максимальной эффективности ГВГ в исследуемом образце на данной длине волны необходим поворот доменной структуры на 3.1 градуса. При этом увеличение эффективности ГВГ в условиях случайного квазифазового синхронизма по сравнению с несинхронной генерацией составляет 1600 раз. Для сравнения показана эффективность ГВГ в идеальной регулярной доменной структуре той же толщины, что и нерегулярная структура в исследуемом образце. Эта эффективность в 8000 раз выше, чем в исследуемом образце, однако, как уже отмечалось, в настоящее время технологии создания таких регулярных структур в SBO не существует; из вышесказанного следует важность разработки такой технологии. Отметим, что спектральная ширина пика случайного квазисинхронизма на длине волны в области 355 нм, в исследуемой доменной структуре составляет порядка 100 ГГц. Такую же ширину имеет пик квазисинхронизма в идеальной регулярной доменной структуре. Это означает, что ограничения на ширину спектра в случае регулярной доменной структуры и рандомизированного образца, исследуемого в нашей работе, практически одинаковы.

Работа выполнена при поддержке Грантов РФФИ 07-02-00497 и 09-02-00690, Грантов Президента РФ в поддержку ведущих научных школ НШ-1011.2008.2, НШ-3818.2008.3, Гранта РНП.2.1.1.1814 и Междисциплинарного интеграционного проекта СО РАН №33.

СПИСОК ЛИТЕРАТУРЫ

1.  Armstrong J.A., Bloembergen N., Ducuing J., Pershan P.S., Phys. Rev. 127, 1918-1939, (1962).

2.  Fejer M. M., Magel G. A., Jundt D. H. and Byer R. L., J. of Quant. Electron. 28, 2631 – 2654, (1992).

3.  Морозов Е. Ю., Каминский А. А., Чиркин А. С., Юсупов Д. Б., Письма в ЖЭТФ 73, 12, 731-734 (2001).

4.  Baudrier-Raybaut M., Haïdar R., Kupecek Ph., Lemasson Ph. and Rosencher E., Nature 432, 374 – 376, (2004).

5.  Vidal X. and Martorell J., Phys. Rev. Lett. 97, 013902, (2006).

6.  Zaitsev A. I., Aleksandrovsky A. S., Vasiliev A. D., Zamkov A. V., J. Crystal Growth 310, 1-4, (2008).

7.  Petrov V., Noack F., Dezhong Shen, Feng Pan, Guangqui Shen, Xiaoqing Wang, Komatsu R., Alex V., Optics Letters 29, 373, (2004).

8.  Aleksandrovsky A. S., Vyunishev A. M., Zaitsev A. I., Zamkov A. V., and Arkhipkin V. G., J. Opt. A. 9, 334–338, (2007).

9.  Oseledchik Yu. S., Prosvirnin A. I., Starshenko V. V., Osadchuk V., Pisarevsky A. I., Belokrys S. P., Korol A. S., Svitanko N. V., Krikunov S. A., Selevich A. F., Optical Material 4, 669-674, (1995).

10.  Bechthold P. S., Haussühl S., Appl. Phys. 14, 403-410 (1977).

Рис. 1. Участок доменной структуры SBO после химического травления (Электронный микроскоп JEOL JSM 7001).

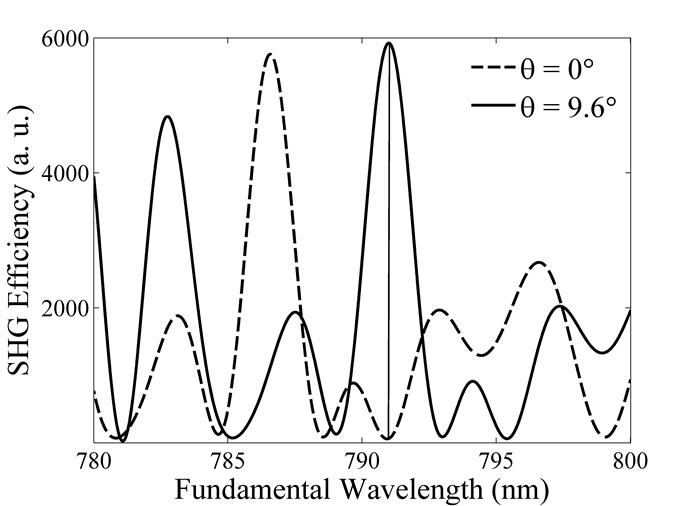
Рис. 2. Эффективность ГВГ вблизи максимума перестроечной кривой Ti:sapphire лазера при падении излучения под разными углами. Пунктирная линия соответствует распространению излучения вдоль кристаллографической оси a (). Сплошная линия соответствует повороту кристалла на угол .

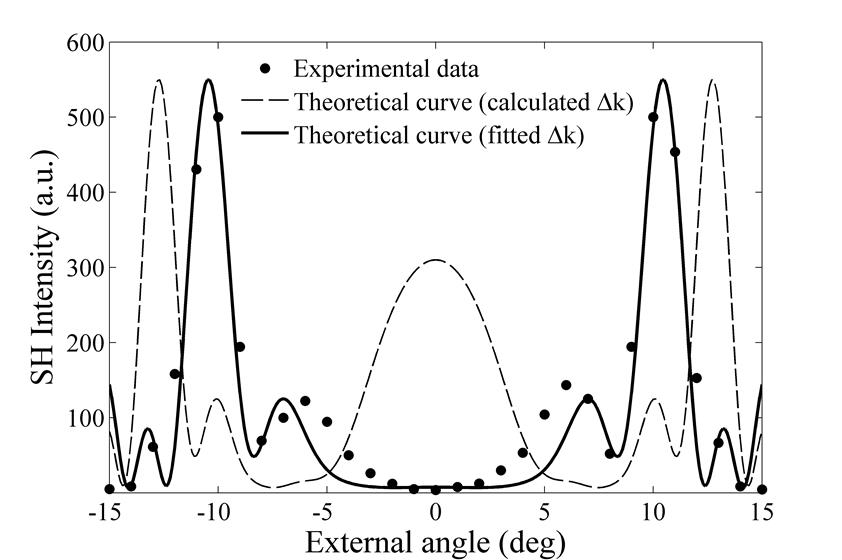
Рис. 3. Угловая зависимость ГВГ в условиях случайного квазифазового синхронизма в нерегулярной доменной структуре SBO. Точками показаны экспериментальные данные. Пунктирная линия – теоретическая кривая при расчетном . Сплошная линия – теоретическая кривая при .

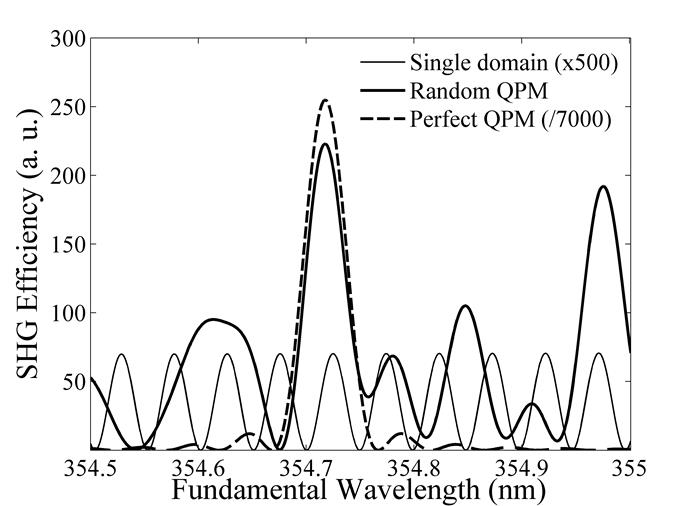
Рис. 4. Спектральная зависимость эффективности ГВГ в области длин волн вблизи 354.7 нм. Тонкая сплошная линия соответствует монодоменному образу. Толстая сплошная линия соответствует нерегулярной доменной структуре в исследуемом образце, повернутом на 3.1 градуса. Пунктирная линия – кривая синхронизма для регулярной доменной структуры.

Александровский Александр Сергеевич

660036 Красноярск, Акадмегородок 50. 8 (391) 2494613

aleksandrovsky@kirensky.ru

Вьюнышев Андрей Михайлович

660036 Красноярск, Акадмегородок 50. 8 (391) 2494613

andre.v@mail.ru

Шахура Ирина Евгеньевна

660041 Красноярск, пр. Свободный 79. 8 (391) 2672781

amatino@rambler.ru

Зайцев Александр Иванович

660036 Красноярск, Акадмегородок 50. 8 (391) 2494425

az@iph.krasn.ru

Замков Анатолий Васильевич

660036 Красноярск, Акадмегородок 50. 8 (391) 2494507

az@iph.krasn.ru