Графом G(X, U) называется совокупность двух множеств X и U, а также отображение X в U (X→U). Здесь X={x1, x2, …, xn} есть совокупность вершин, U={u1, u2, …, um} — совокупность ребер, а отображение j: X→U устанавливает однозначное соответствие между множествами X и U.
Вес ребра — это число, которое можно интерпретировать как длину, пропускную способность, стоимостные затраты и т.п. Отдельное ребро может иметь несколько весов, характеризующих разные свойства (атрибуты) ребра.
Дуга — это ориентированное ребро графа.
Маршрут между вершинами xi и xj — это упорядоченная совокупность ребер, которые удовлетворяют следующим условиям:
à первое ребро начинается в вершине xi;
à концом последнего ребра является вершина xj;
à конец предыдущего ребра соединяется с началом последующего ребра в некоторой вершине.
Маршрут можно также описать последовательностью вершин, через которые он проходит.
Цепь — это маршрут, в котором все ребра различны.
Цикл в графе — это цепь, у которой начальная и конечная вершины совпадают.
Дерево графа — это связный граф без циклов.
Метрическое пространство[1] M есть множество точек с функцией расстояния d (также называется метрикой). Для любых точек x, y и z из пространства M эта функция должна удовлетворять следующим условиям:
1. d(x, x)=0 (расстояние от вершины до самой себя равно 0) или d(x, y)=0 при x=y (аксиома тождества или рефлексивности)
2. d(x, y) = d(y, x) (аксиома симметрии)
3. d(x, z) £ d(x, y) + d(y, z) (аксиома транзитивности или неравенство треугольника).
Эти аксиомы отражают интуитивное понятие расстояния. Например, расстояние должно быть неотрицательно, т.е. d(x, y)³0 (это вытекает из аксиомы треугольника при z=x) и расстояние от x до y такое же, как от y до x.
Неравенство треугольника означает, что прямое расстояние от x до z не должно быть длиннее, чем при движении от x до z через точку y.
Если для весов ребер использовать аддитивные характеристики, то длина маршрута равна сумме весов входящих в него ребер.
Расстояние ρ(xi, xj) между вершинами xi и xj равно длине кратчайшего маршрута между этими маршрутами.
Эксцентриситет вершины xi — это максимальное расстояние от вершины xi до какой-то другой вершины графа G:
ε(xi) = max ρ(xi, xj), xjÎX.
Диаметр графа G — это максимальный из эксцентриситетов для его вершин:
d(G) = max ε(xi), xiÎX.
Радиус графа G — это минимальный из эксцентриситетов для его вершин:
r(G) = min ε(xi), xiÎX.
Центром графа (или центральной вершиной) называется такая вершина, для которой эксцентриситет равен радиусу графа. В общем случае граф может иметь несколько центров.
Граф называется связным только в случае, когда для любой пары вершин графа имеется хотя бы один маршрут.
Вершины xi и xj в графе G называются k-связанными, если рассматриваемые вершины остаются связанными при удалении (k-1) других вершин.
Вершины xi и xj в графе G называются реберно k-связанными, если эти вершины остаются связанными при удалении (k-1) ребер графа.
Две цепи между вершинами xi и xj называются независимыми, если они не содержат общих вершин (кроме xi и xj).
Теорема Менгера. Вершины xi и xj в графе G k-связаны только в случае, когда между ними существует k независимых цепей.
Связывающая сеть (каркас, остов, скелет графа) — такая часть исходного графа, при которой обязательно охватываются все его вершины. Кратчайшая связывающая сеть имеет минимальное значение для суммарной длины ребер. Доказано, что при отсутствии особых требований к связности такая сеть имеет структуру дерева, т.е. для каждой пары вершин есть только одна цепь. Может быть построена с помощью алгоритма Прима–Краскала.
Модифицированный алгоритм Прима–Краскала
Может использоваться для построения кратчайшей связывающей сети, у которой по условиям решения задачи требуемая связность должна быть больше 1.
Порядок действий:
1. Упорядочить ребра в порядке убывания их весов.
2. Согласно полученной последовательности просмотреть все ребра и по каждому из них принять решение, удалять ребро или оставить его в графе. Ребро удаляется только в том случае, если после этого оставшиеся пути будут обеспечивать требуемый уровень связности графа.
Пример. Построить связывающую сеть, в которой при минимальной стоимости обеспечивается не менее 2 независимых путей для каждой пары вершин.
Передаточное число для вершины xi в графе G вычисляется по следующей формуле:
s(xi)
= 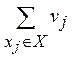 ρ(xi,
xj),
ρ(xi,
xj),
где vj — вес вершины xj.
Медианой графа G называют вершину xs, для которой передаточное число s(xs) принимает минимальное значение:
s(xs)
= 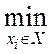 s(xi).
s(xi).
Понятие b-медианы
Пусть XbÎX — некоторое подмножество вершин в графе G, состоящее из b вершин. Расстояние от некоторой вершины xi до этого подмножества определим следующим образом:
ρ(xi, Xb)
= 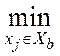 ρ(xi, xj),
ρ(xi, xj),
т.е. расстояние от вершины xi до некоторого подмножества вершин Xb вычисляется как расстояние от этой вершины до ближайшей вершины, которая принадлежит подмножеству Xb.
Тогда передаточное число для подмножества вершин Xb в графе G будем вычислять по следующей формуле:
s(Xb)
= 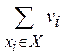 ρ(xi,
Xb),
ρ(xi,
Xb),
Подмножество ![]() , для которого передаточное число s(
, для которого передаточное число s(![]() ) принимает
минимальное значение, т.е. s(
) принимает
минимальное значение, т.е. s(![]() ) =
) = 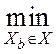 s(Xb), называется b-медианой
графа G. Любая вершина в составе
s(Xb), называется b-медианой
графа G. Любая вершина в составе ![]() называется медианной вершиной.
Остальные вершины называют немедианными, и каждая из них прикрепляется к ближайшей
медианной вершине.
называется медианной вершиной.
Остальные вершины называют немедианными, и каждая из них прикрепляется к ближайшей
медианной вершине.
[1] Понятие метрического пространства впервые ввёл Морис Фреше.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.