5.3. Проверить правильность составления схемы.
5.4. Запустить временной анализ (меню «Analysis» —> «Transient»).
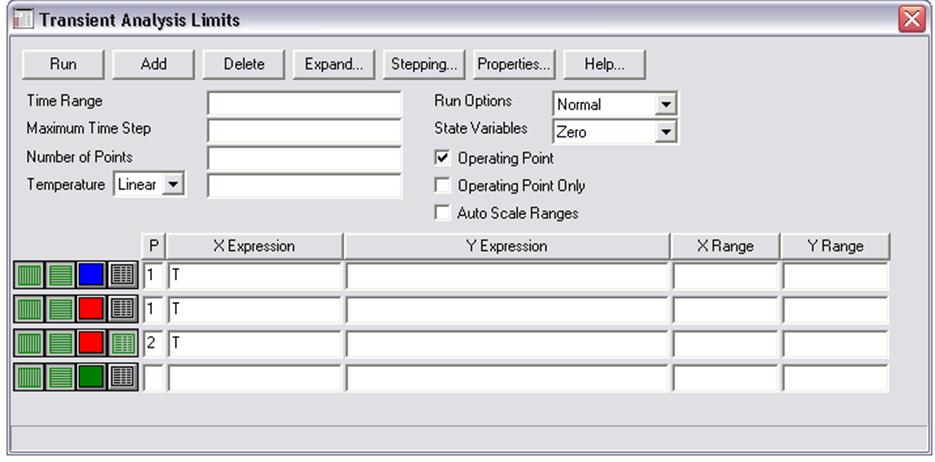
5.5 Проверить правильность заданных данных для построения графиков. В графе «X Expression» должно быть указано время «Т». В графе «Y Еxpression» должны быть указаны графики тактовой последовательности, М-последовательности [графики логического уровня сигнала в соответствующих узлах схемы - «d(номep узла)»] и ее АКФ [«ас(v(номер узла))»] на ширине периода Период указан в графе «Time Range». В графах «X Range» и «Y Range» задается масштаб графиков. В графе «Р» - номер графика, можно вывести результаты моделирования как на одном графике, так и на нескольких.
5.6. Вывести графики на экран монитора (нажав «Run» в левом верхнем
углу окна) и зарисовать их.
5 7. Повторить операции 5.2-5.6 с файлами М-посл., (K=4).cir, М-посл.,(К=5). cir.
6. Содержание отсчета.
Отсчет должен содержать:
1. Цель работы.
2. Исследуемые схемы.
3. Графики образованных последовательностей и их АКФ.
4 Выводы по работе.
7. Контрольные вопросы.
1. Что из себя представляет М-последовательность?
2. Каковы основные свойства М-последовательности?
3. Как строится АКФ М-последовательности?
4. Как выглядит схема цифрового автомата М-последовательности?
Лабораторная работа №3.
Исследование нелинейных последовательностей.
1.Цель работы: изучить способы формирования нелинейных последовательностей длины, их свойства, исследовать их автокорелляционные функции при различном числе элементов (символов) в периоде.
2. Литература
1 Варакин Л.Е. «Системы с шумоподобными сигналами».
М : «Радио и связь», 1985.-384с.
2. Конспект лекций.
3. Домашнее задание.
1. Изучить основные свойства нелинейных последовательностей испособы их формирования.
2. Рассчитать АКФ усеченной нелинейной последовательности, под которойпонимается непериодическая последовательность длиной в период N..
Таблица 2.1. Варианты для выполнения домашнего задания
|
Вариант |
Последовательность |
|
1.6 |
{-1,-1,1,-1,1,1,1} |
|
2.7 |
{-1-1,1,-1,1,1,1,-1} |
|
3.8 |
{-1,-1,-1,1,-1,-1,1,1,-1,1,-1,1,1,1.1} |
|
4.9 |
{-1-1,-1,1,-1,-1,1,1,-1,1,-1,1,1,1,1,-1} |
|
5.0 |
{-1,-1,1,1,1,-1,1} |
Вариант выбирается по последней цифре номера зачетной книжки.
4.Описание лабораторного макета.
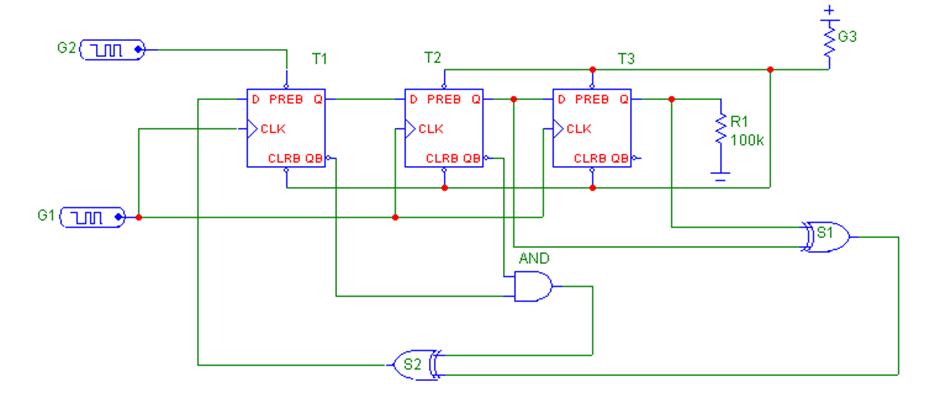
Рис. 2.2 Цифровой автомат формирования нелинейной последовательности.
Изучаемая схема представляет из себя
регистр с нелинейной обратной связью и состоит из набора триггеров,
осуществляющих задержку входного символа на один такт сумматоров по модулю 2
и схемы И, Число триггеров определяет период нелинейной
последовательности
, где К -
число триггеров. Период увеличивается по сравнению с М-последовательностью,
поскольку путем дополнительных логических операций в схеме регистра перестает
быть запрещенной комбинация из К нулей (000...0). Выходы триггеров
подключенных к сумматору определяются, также как и для М-последовательности, в
соответствие с характеристическим многочленом. Генератор G2 является запускающим, с него
подается «1» на вход первого триггера, запуская работу схемы. На следующем
такте эта «1» сдвигается, поступая на вход второго триггера, а на вход первого
триггера поступает символ с сумматора S2. Кроме того, инверсные сигналы с инверсного выхода всех
триггеров, кроме последнего поступают на схему И. На выходе схемы
И символ «1» появится только тогда, когда инверсные символы триггеров
Т1, Т2...
, принимают значение 1 При любых
других комбинациях инверсных символов Т1Т Т2... , на выходе схемы И
будет символ «0». Символ с выхода схемы И поступает на дополнительный
сумматор по mod 2,
обозначенный на схеме S2, на второй вход сумматора поступает сумма символов цепи обратной
связи регистра. Так как цепь обратной связи замкнута, то в схеме возможны
колебания. Можно показать, что в регистре будет иметь место все кодовые
комбинации длиною К символов, в том числе и комбинация со зсеми нулями.
Таким образом, состояния логических в схеме (с К=3) будут следующие.
Таблица 2.3. Состояния регистра с нелинейной обратной связью
|
№ |
Вход |
Выход |
||||||
|
такта |
Т1 |
Т1 |
Т2 |
T3 |
Т |
Т |
& |
S1 |
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
|
2 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
|
3 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
4 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
|
5 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
6 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
|
7 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
|
8 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
|
9 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
10 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
Таким образом, если символы непрерывно считывать с выхода ТЗ, то получим периодическую нелинейную последовательность
...00101110001011100010111... (2.2)
с периодом ,
5. Порядок выполнения работы.
5 1. Запустить программу Micro-Cap 7.
5.2. В меню «file» выбрать «open» и щелкнуть мышкой на файл нелинейная посл (K=3).cir
5.3. Проверить правильность составления схемы.
5.4. Запустить временной анализ (меню «Analysis» —> «Transient»).
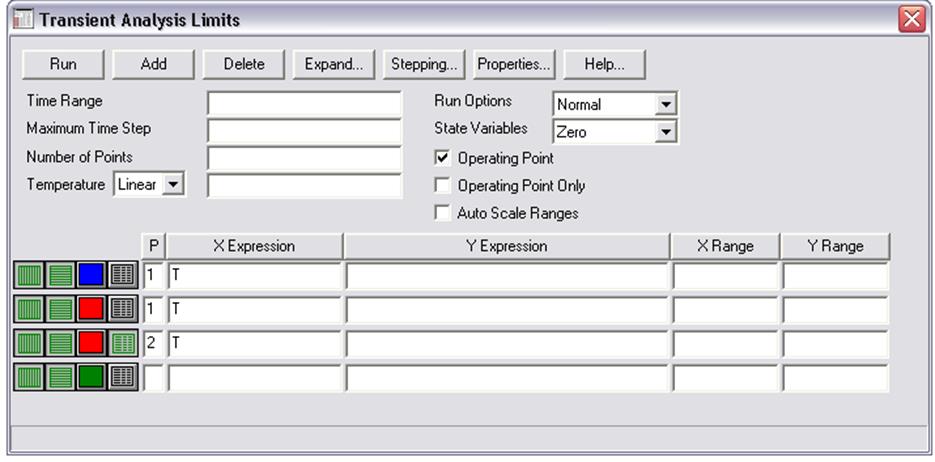
5.5 Проверить правильность заданных данных для построения графиков. В графе «X Expression» должно быть указано время «Т». В графе «Y Еxpression» должны быть указаны графики тактовой последовательности, нелинейной последовательности [графики логического уровня сигнала в соответствующих узлах схемы - «d(номep узла)»] и ее АКФ [«ас(v(номер узла))»] на ширине периода. Период указан в графе «Time Range». В графах «X Range» и «Y Range» задается масштаб графиков. В графе «Р» - номер графика, можно вывести результаты моделирования как на одном графике, так и на нескольких.
5.6. Вывести графики на экран монитора (нажав «Run» в левом верхнем углу окна) и зарисовать их.
5 7. Повторить операции 5.2-5.6 с файлами Нел-посл (K-4).cir, Нел-посл (K=5).cir
6. Содержание отсчета.
Отсчет должен содержать:
1. Цель работы.
2. Исследуемые схемы.
3. Графики образованных последовательностей и их АКФ. 4 Выводы по работе.
7. Контрольные вопросы.
1. Что из себя представляет нелинейная последовательность?
2. Каковы основные свойства нелинейной последовательности?
3. Как строится АКФ нелинейной -последовательности?
4 Как выглядит схема цифрового автомата нелинейной последовательности?
5. Почему период нелинейной последовательности больше периода М-последовательности при том же числе разрядов регистра (триггеров в схеме)?
6. Какая из двух последовательностей, рассмотренных в лаб.,раб.,№2 и №3 обладает лучшими корреляционными свойствами и почему?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
1