Математическое моделирование в среде MatLab. Эффективный съем данных

1. Построить график модели, если параметры и базисный вектор модели известны.

Базисный вектор модели имеет вид:

f=[1,X(1),X(1)^2,X(1)^3]

(1.1)

Вектор истинных значений параметров:   Q=[9 -4 -3 0.5];

Модель находится в области:    X=[0:0.1:10];

График модели представлен на рис. 1.

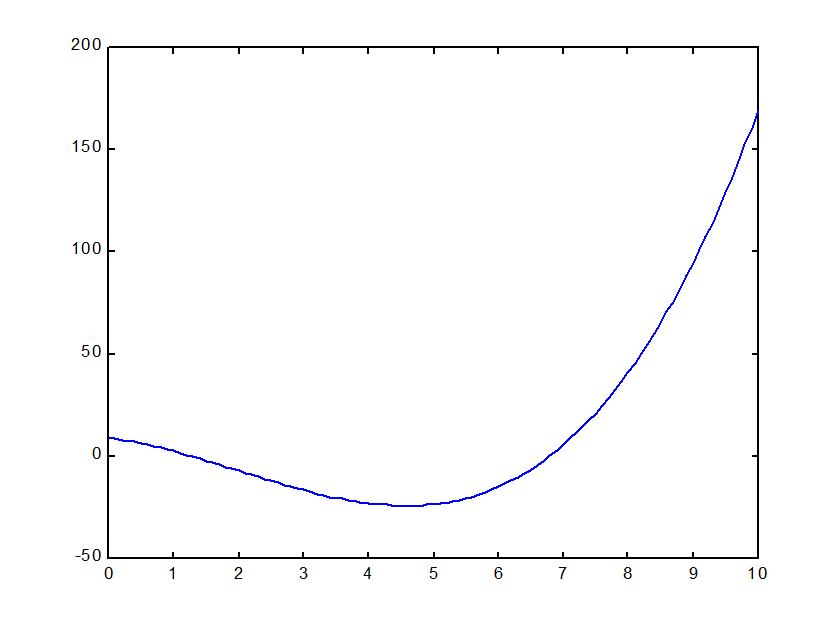
Рис. 1. График модели представленной вектором (1.1)

Текст программы представлен в файле point.m

2.  Смоделировать съём данных с объекта в определённых точках.

Среднеквадратическое отклонение ошибки наблюдения  sigma = 1.5.

Матрица аргументов модели.

PLAN =

0	6.0000
2.7650	6.0000
7.2350	6.0000
10.0000	6.0000

Матрица сгенерированных случайных чисел с нулевым математическим ожиданием и среднеквадратическим отклонением sigma, размерностью 7*4.

rnd =

0.1214	0.5403	0.2164	-0.5928
-1.4789	-2.9268	2.2329	1.7854
-0.6467	1.8546	-1.0684	-0.0249
0.2277	-0.1769	0.0118	-1.1130
-4.1920	-0.6298	-0.0294	-1.1467
2.0813	2.6337	0.5012	2.5423
1.3137	0.2905	0.7704	-3.0638

Смоделированный массив данных:

Ymodel =

9.1214	-14.9664	12.5996	168.4072
7.5211	-17.3530	14.6161	170.7854
8.3533	-12.5715	11.3148	168.9751
9.2277	-14.6030	12.3950	167.8870
4.8080	-15.0559	12.3538	167.8533
11.0813	-17.0599	12.8844	171.5423

Текст программы представлен в файле point1.m

3.  Построить график (гистограмму) распределения ошибки, сделать предположение о виде распределения.

График распределения ошибки представлен на рис. 2.

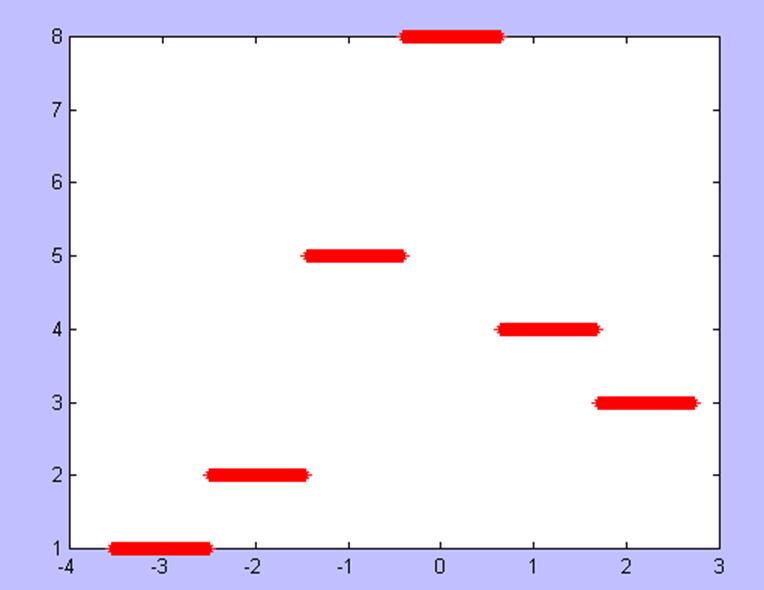
Рис. 2. График распределения ошибки.

      Вид гистограммы говорит о том, что наиболее вероятное значение ошибки находится в центре размаха варьирования. Остальные значения ошибки распределены почти симметрично относительно наиболее вероятного. Это позволяет выдвинуть гипотезу, состоящую в том, что данное распределение ошибки приближенно нормально. Из графика видно, что математическое ожидание находится в интервале от 0 до 0,5. Таким образом, в качестве вида распределения можно предположить – нормальное распределение (или распределение Гаусса) с математическим ожиданием примерно равным 0,3.

Текст программы представлен в файле point1.m

4.  Рассчитать параметры модели в соответствии со снятыми данными.

Параметры модели, рассчитанные  методом МНК

q_or =  8.3521

           -4.3646

           -2.8702

            0.4916

Параметры модели, рассчитанные  методом ВМНК

q_w =  8.3521

           -4.3646

           -2.8702

            0.4916

Количество модельных расчетов равно 9.

График анализа апостериорной и априорной дисперсии ошибок представлен на рис. 3.

Текст программы представлен в файле point2.m

5.  Анализ апостериорной дисперсии ошибок наблюдений.

Количество модельных расчетов равно 45.

График представлен на рис. 4.

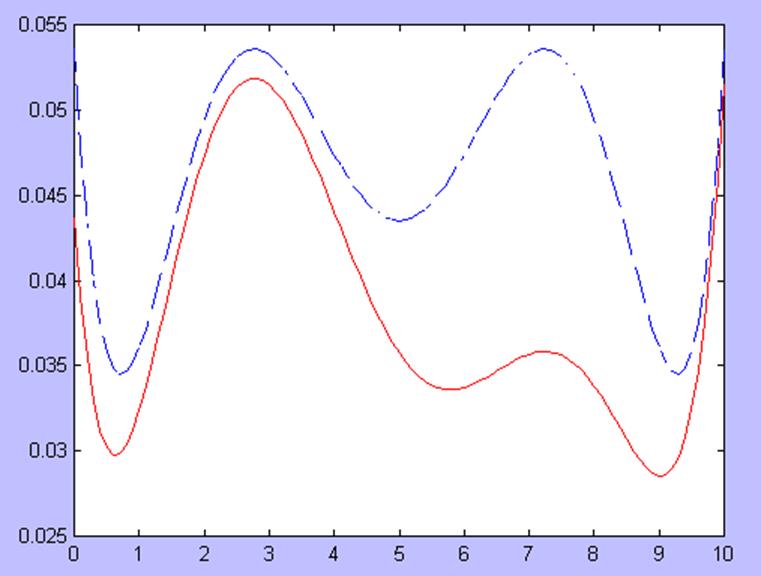
Рис. 3. Анализ апостериорной дисперсии ошибок  для 9 наблюдений (красная линия – с учетом апостериорной информации; синяя – соответствует критерию оптимальности).

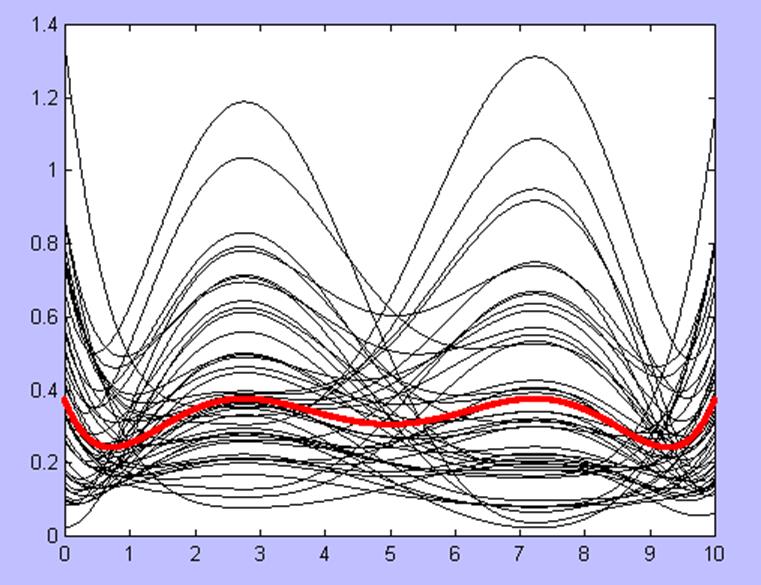
Рис. 4. Анализ апостериорной дисперсии ошибок 45 наблюдений (черные линии – с учетом апостериорной информации; красная – соответствует критерию оптимальности).

Текст программы представлен в файле point2.m

6.  Сравнение априорной и апостериорной дисперсии

Визуальное сравнение параметров априорной и апостериорной дисперсиями представлено на рис.5 и рис.6.

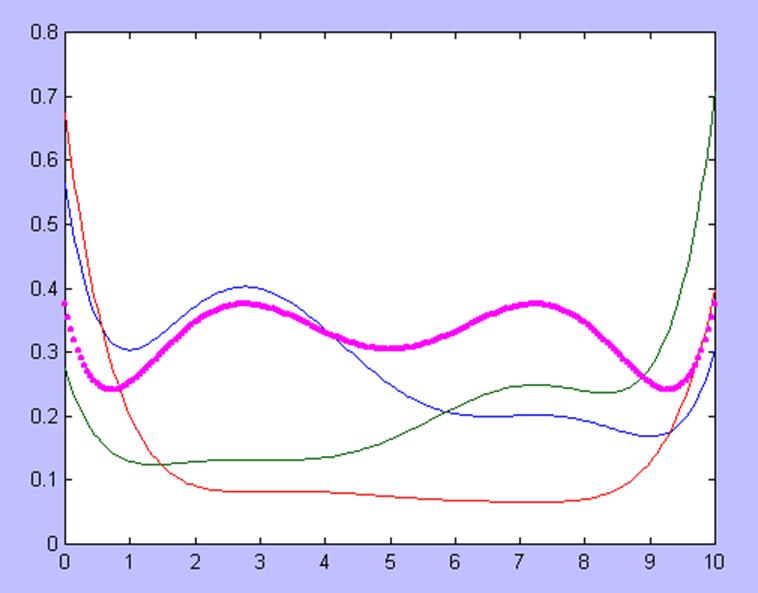
Рис. 5. Сравнение априорной и апостериорной дисперсии (лиловая линия, жирная – априорная дисперсия; остальные – апостериорная)

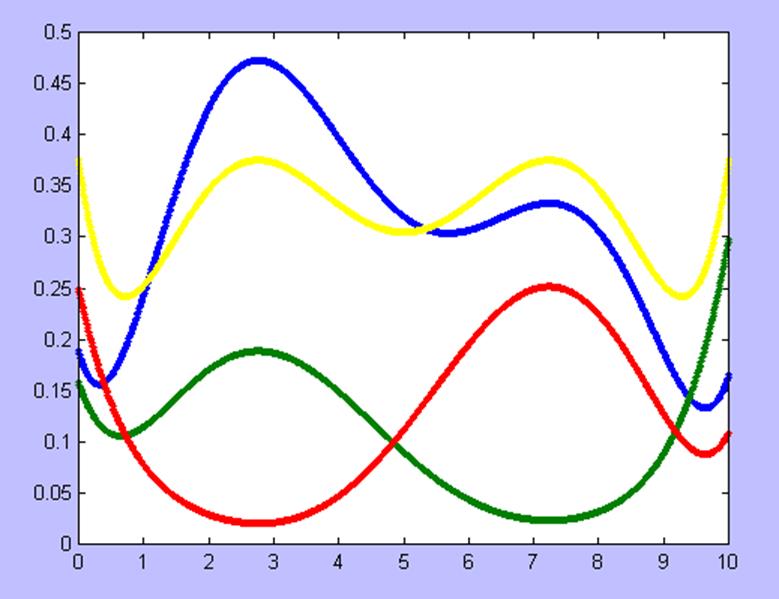
Рис. 6. Сравнение априорной и апостериорной дисперсии (желтая линия – априорная дисперсия, остальные - апостериорные).

Как показано на рис.5 и рис. 6 для D-оптимальных планов отличие между априорной и апостериорной дисперсиями оценок моделей может быть существенным. Для анализа рассмотрим поведение графиков, представленных на рис.6. Как видно из графика, представленного на рис. 6 красной линией. На этом графике апостериорная дисперсия для всех значений x (из области X) меньше априорной. Аналогично поведение графика апостериорной дисперсий, обозначенного зеленой линией.

Отсюда можно сделать вывод, что D-оптимальность плана в соответствии с априорным критерием оптимальности не гарантирует (даже в случаях, когда базис модели точно известен) оптимальности этого же плана по апостериорным данным, т.е. оптимальный план фактически (в действительности, реально) может таковым не являться.

Текст программы представлен в файле point3.m.

7.  Исследовать сходимость эффективных стратегий снятия данных.

Определяется влияние изменения количества точек просчета на априорную функцию дисперсии оценки отклика и апостериорные функции дисперсии оценки отклика.

Для исследования определяются следующие параметры:

1)  Абсолютное отклонение между этими функциями.

(7.1)

2)  Относительное отклонение между функциями.

(7.2)

На основе определенных параметров рассчитываются следующие характеристики различия априорной и апостериорных дисперсий оценок функций отклика:

1)  - наибольшее значение среди наибольших на X разностей  за определенное количество модельных просчетов при определенном значении  (красная линия);

2)  - среднее значение наибольших на X разностей  за определенное количество модельных просчетов при определенном значении  (зеленая линия);

3)   - среднее значение среди наименьших на X разностей  за определенное количество модельных просчетов при определенном значении  (желтая линия);

4)   - наименьшее значение среди наименьших на X разностей  за определенное количество модельных просчетов при определенном значении  (синяя линия);

5)   - среднее значение наибольших на X разностей за определенное количество модельных расчетов при определенном значении  (голубая линия);

6)   - среднее значение среди наименьших на X разностей  за определенное количество модельных просчетов при определенном значении  (лиловая линия);

На рис. 7 и рис.8 приведен вид этих характеристик различия априорной и апостериорных дисперсий оценок функций отклика (для D-оптимального плана) при следующих значениях:

Количество измерений в каждой точке плана варьируется от 10 до 60. Количество повторных вычислений (модельных просчетов) равно 50 при значении =1,5.

Из графиков видно, что при увеличении количества расчетов в каждой точке плана значения характеристик различия априорной и апостериорных дисперсий оценок функций отклика уменьшаются. Т.е. чем больше количество точек съема данных, тем ближе приближаются моделируемые модели к базисной.

Текст программы представлен в файле point4.m.

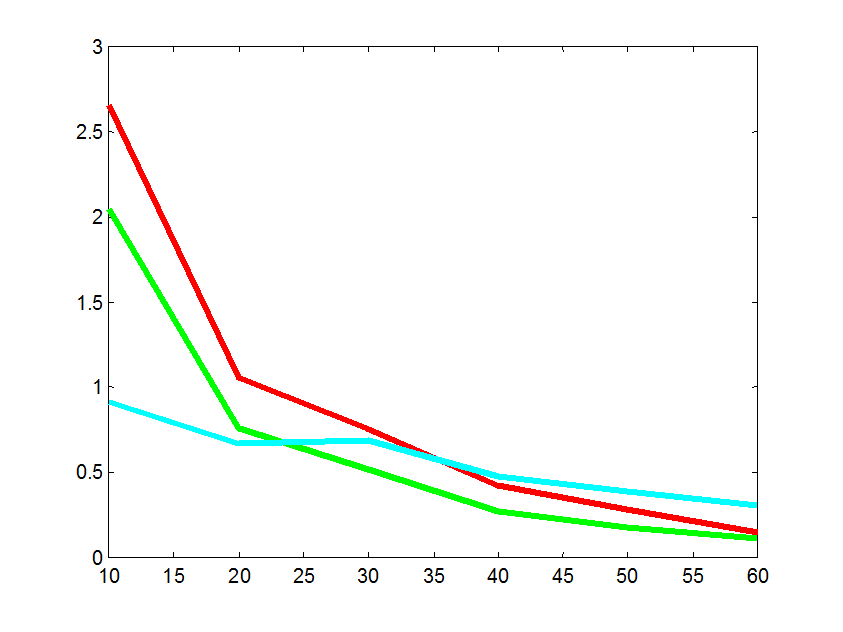
Рис. 7 Характеристики различия дисперсий в зависимости от N.

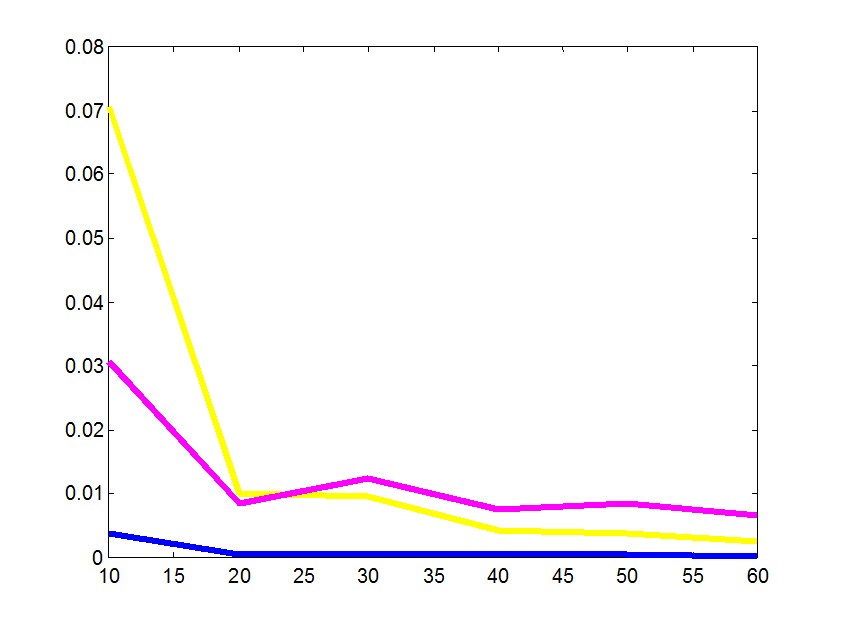
Рис. 8 Характеристики различия дисперсий в зависимости от N.

Определяется влияние изменения параметра  на априорную функцию дисперсии оценки отклика и апостериорные функции дисперсии оценки отклика.

      Рассчитываются параметры заданные формулами (7.1) и (7.2). На их основе рассчитываются характеристики различия априорной и апостериорных дисперсий оценок функций отклика 1)- 6).

      На рис. 9 и рис.10 приведен вид этих характеристик различия априорной и апостериорных дисперсий оценок функций отклика (для D-оптимального плана) при следующих значениях:

Количество измерений в каждой точке плана равняется 9. Количество повторных вычислений (модельных просчетов) равно 50 при варьировании значения  от 0,5 до 5,5.

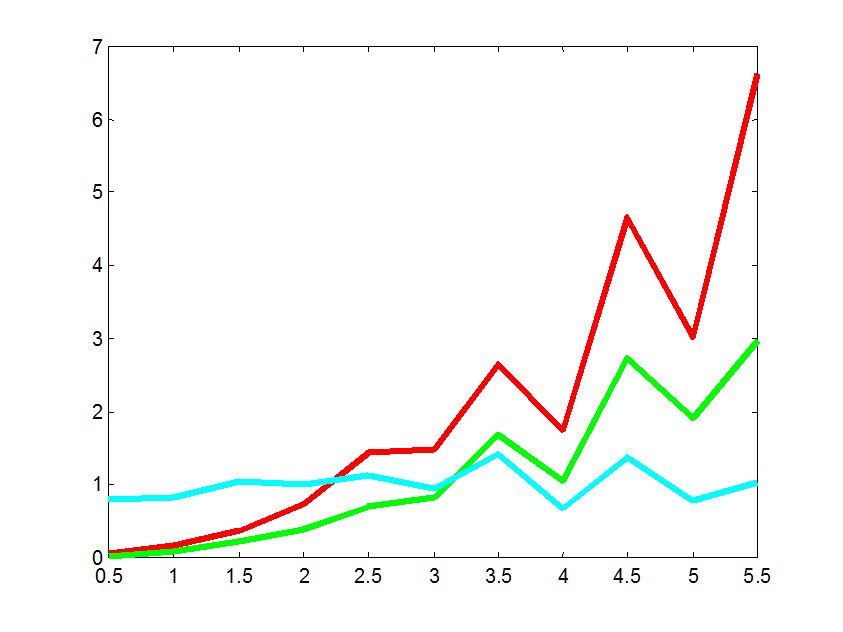
Рис. 9 Характеристики различия дисперсий как функции .

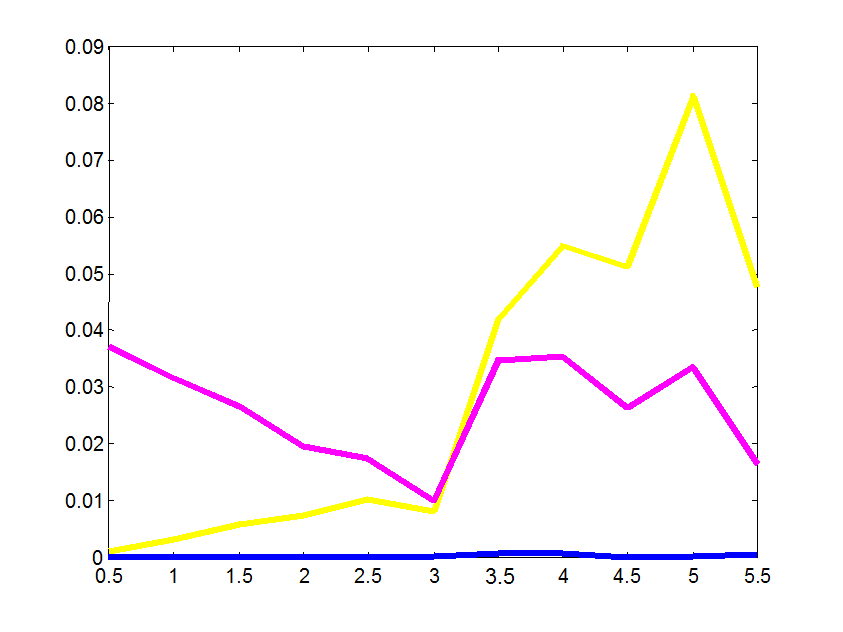
Рис. 10 Характеристики различия дисперсий как функции .

Из графиков, представленных на рис. 9 и рис. 10 видно, что при увеличении значения параметра  величина характеристик различия априорной и апостериорных дисперсий оценок функций отклика увеличивается. Т.е. более точное моделирование параметров базисной модели получается при маленьких значениях .

Анализ полученных результатов и выводы по работе:

Оптимальные планы экспериментов в некоторых случаях таковыми могут не являться, так как для них не выполняются теоремы эквивалентности и оптимальности, если заменить априорные значения дисперсий на апостериорные. Таким образом, можно утверждать, что оптимальных планов вообще не существует, и они будут являться условно оптимальными до тех пор, пока не подтвердятся в результате экспериментов.

В свою очередь, для получения опытных данных, близких к базовой модели, необходимо выбирать правильные параметры для проведения экспериментов. В частности брать значение параметра разброса (среднего квадратичного отклонения) значений случайной составляющей близкой к нулю. И увеличивать количество расчетов в каждой точке плана экспериментов.