Магнитные свойства конденсированных веществ, страница 2

Здесь m_l - магнитное квантовое число, g - фактор спектроскопического расщепления Ланде, называемый обычно g-фактором. Он представляет собой отношение магнитного момента системы, выраженного в магнетонах Бора m_B, к механическому моменту количества движения системы, выраженному в единицах . Для электронного спинового магнетизма g = 2, для чисто орбитального магнетизма g = 1.

У атомов и ионов с полностью заполненными электронными оболочками результирующие спиновые и орбитальные моменты, а, следовательно, и полный магнитный момент атома М_а равны нулю. Они диамагнитны.

Атомы и ионы с недостроенными внутренними оболочками, а также с нечетным числом электронов в валентной оболочке, характеризуются отличным от нуля результирующим атомным магнитным моментом. Сюда относятся переходные и редкоземельные элементы. Не равен нулю магнитный момент и у атомов с некомпенсированными спиновыми моментами, например, у атомов кислорода. Такие атомы парамагнитны, в конденсированном состоянии вещества из таких атомов могут быть как парамагнитными, так и ферромагнитными.

2.5.2. Диамагнетизм изолированных атомов и диэлектрических конденсатов

Физическую природу диамагнетизма связывают с изменением характера движения электронов. Поскольку электроны входят в состав любых веществ, постольку "электронный" диамагнетизм является наиболее общей реакцией материи на воздействие магнитного поля. Он часто бывает незаметен на фоне более интенсивных эффектов, объясняемых пара- и ферромагнетизмом, но в веществах, у атомов которых полный магнитный момент равен нулю, диамагнетизм является единственным типом отклика на внешнее магнитное поле, здесь он проявляется в чистом виде.

Классических представлении об атоме как о системе электронов, движущихся вокруг ядра по фиксированным замкнутым траекториям - орбитам, оказывается достаточно не только для выяснения физической природы диамагнетизма, но и для грубой количественной оценки величины восприимчивости диамагнетиков. Представим круговую электронную орбиту в качестве витка с током (рис.2.5.2), где электрон движется с угловой скоростью w₀ = v/r. Орбиту можно представить как контур с орбитальным магнитным моментом  и антипараллельным ему механическим моментом . Из общефизических представлений следует, что наложение на атом медленно меняющегося или постоянного магнитного поля изменяет характеристики движения электрона - радиус орбиты остается неизменным, а угловая скорость w₀  несколько изменяется (уменьшается или увеличивается в зависимости от взаимной ориентации  и ) .

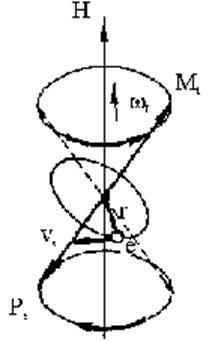
Рис.2.5.2. Прецессия электронной орбиты во внешнем магнитном поле

В общем случае, когда Н  не перпендикулярно плоскости орбиты, действие поля, как показал Лармор, состоит в возбуждении прецессии орбиты вокруг вектора  , подобной той, которая наблюдается при затухании вращения механического волчка. Расчет показывает, что угловая частота w_L такой прецессии определяется напряженностью магнитного поля Н  и составляет

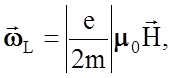                                                                      (2.5.9)

где  e и m - заряд электрона и его масса. Вектор  описывает конус вокруг , причем направления  и   совпадают.

Рассматривая прецессию электронной орбиты вокруг  как дополнительное движение электрона с частотой n_L, создающее дополни-

тельный замкнутый ток, 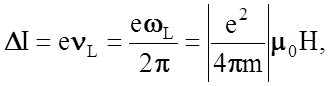направленный против основного орбитального тока, приходим к выводу о взаимодействии во внешнем магнитном поле Н  индуцированного элементарного орбитального магнитного момента

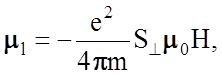                                                               (2.5.10)

направленного антипараллельно . Здесь S_^ - проекция площади орбиты на плоскость, перпендикулярную вектору Н. Показано, что S_^  = 2/3p<r²>, где <r²>, - средний квадрат расстояния электрона от ядра. Тогда вместо уравнения (2.5.10) можно записать для магнитного момента одного электрона, наведенного полем Н:

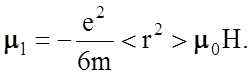                                                         (2.5.11)

Для атома с порядковым номером 2  наведенный орбитальный момент равен векторной сумме наведенных орбитальных моментов электронов:

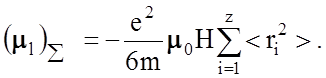                                              (2.5.12)

По сути дела атом с циркулирующими в нем электронами ведет себя подобно индуктивности, в которой, в соответствии с правилом Ленца, в момент включения магнитного поля возникла э.д.с. противоположного знака. Поскольку электроны движутся в вакууме и никакого сопротивления не испытывают, возросшая или уменьшившаяся их скорость с течением времени не изменяется вплоть до изменения или выключения внешнего магнитного поля. В объеме тела формируется внутреннее поле, направленное против внешнего; суммарное поле B_å меньше, чем поле в вакууме.

По определению, магнитная восприимчивость вещества составляет 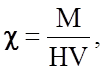 где M - магнитный момент объема V. Классический  расчет Ланжевена дает величину магнитной восприимчивости единицы объема, содержащей N атомов с номером Z   (в Си):

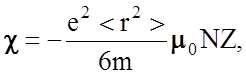                                                          (2.5.13)

которая подтверждается и квантово-механическим расчетом.

Оценим величину c для диамагнитного твердого тела. Пусть параметр решетки  a » 2<r> = 2Å , то есть <r> » 1Å = 10^-10 м. Тогда для атомов с номером Z  сомножитель перед Н  в уравнении (5.11) составляет ~ 5Z×10^-35 м². Так как твердое тело содержит приблизительно N = 10²⁸ – 10²⁹ атомов на 1 м³, то магнитная восприимчивость c  составит около Z×(10^-6 –10^-5), что точно отражает порядок величины (см. табл. 2.5.1).

Индуцированный "электронный" диамагнетизм - явление упругое, выключение внешнего магнитного поля приводит к исчезновению наведенных магнитных моментов атомов, ликвидации прецессии электронных орбит.