Существуют различные приемы построения счетчиков. Например, если модуль счета К можно представить в виде произведения двух чисел А и В, то можно построить 2 счетчика соответственно с такими модулями и включить их последовательно. Иногда это упрощает проектирование, но требует большее число триггеров. Например:
15 = 5 х 3. Для построения счетчика на 15 необходимо минимально 4 триггера. Для делителя на 5 необходимо 3 триггера и для делителя на 3 – 2 триггера, т.е. общее число триггеров – 5. Однако сложность схемы зависит также от числа дополнительных логических элементов, которые обеспечивают необходимые обратные связи в схеме.
Схемные решения счетчиков с произвольным коэффициентом деления могут быть различными. Рассмотрим некоторые из них.
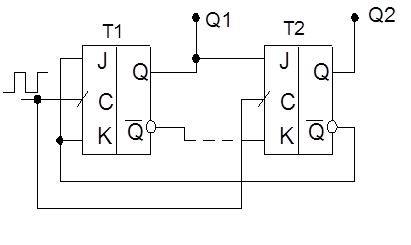Счетчик делитель на
3.
Таблица состояний.
 |
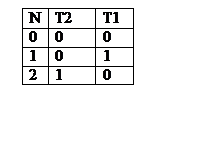
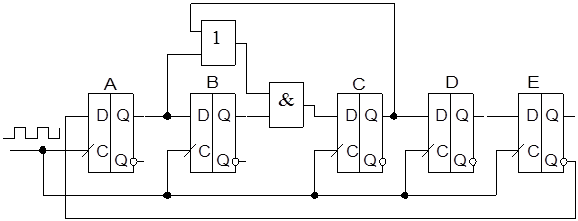
Изучая таблицу состояния, можно увидеть, что при переходе из состояния 2 в начальное состояние 0, необходимо запретить переключение триггера Т1, а триггер Т2 переключить в состояние лог 0. Кроме того, можно видеть, что триггер Т2 повторяет состояния Т1 через 1 такт, т.е. работает в режиме D – триггера. Схему счетчика необходимо проверять как она выходим из двоичных состояний, которые не относятся к рабочим, так как возможно существование нерабочих циклов и тупиковых состояний, из которых счетчик не сможет выйти на рабочий цикл естественным путем.
Использование универсальных счетчиков при произвольном модуле деления.
Большинство современных счетчиков имеет возможность параллельной записи числа, возможность сброса разрядов счетчика в 0, существует много реверсивных счетчиков, поэтому большинство задач по созданию счетчиков с произвольным коэффициентом деления можно решить при минимальном числе дополнительной логики, или пользуясь только выходами и входами управления счетчиков.
Пример: необходимо построить счетчик – делитель на 137, причем этот счетчик работает по циклу, в котором разрешены состояния от 19 до 155.
Используем универсальные счетчики 1533 ИЕ10. Счетчики имеют синхронную предустановку числа и асинхронный сброс.
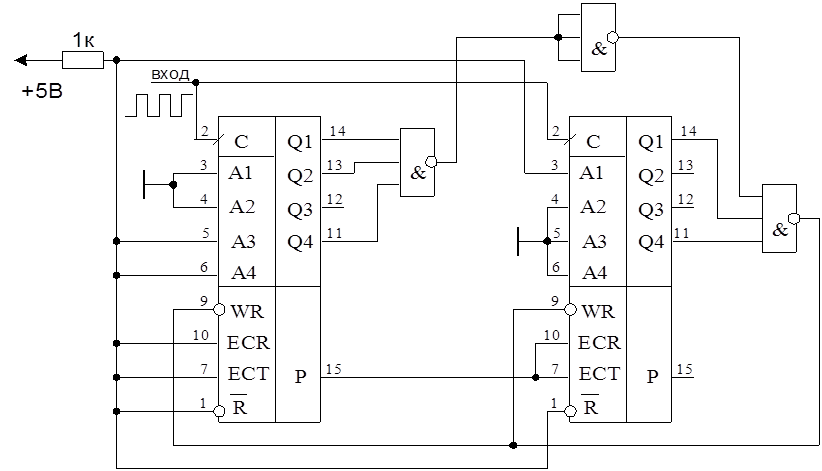
Представляем числа 19 и 155 в двоичном коде:
19=16+2+1=24+21+20=10011
155=128+16+8+2+1=27+24+23+21+20=1001 1011
На входах параллельной записи устанавливаем число 15= 0001 0011
Схема на логических элементах 3И-НЕ имеет лог.1 на выходном вентиле во всех состояниях, кроме состояния с числом 155 = 1001 1011. Когда счетчик достигает этого значения, на входе параллельной записи счетчиков устанавливается лог.0, что соответствует режиму параллельной записи. По фронту следующего импульса синхронизации в счетчик записывается число 15, и затем счетчики начинают суммировать импульсы, поступающие на вход. Далее цикл повторяется.
Хотя двоичная система исчисления имеет многие преимущества и широко используется в ЭВМ, однако при больших объёмах вводимой и выводимой информации часто удобно использовать десятичную систему исчисления, поскольку большая часть данных – в десятичной форме. С целью упрощения общения человека с машиной разработан ряд десятичных кодов.
Для цифр 0, 1, 2,…, 9 в двоичной форме необходимо иметь по крайней мере 4 двоичных разряда. Так как возможны 16 комбинаций у 4-ёх разрядного двоичного числа, из которых используются только 10, можно построить очень много различных кодов. Особых интерес представляют взвешенные коды – такие, у которых каждому двоичному разряду приписывается вес, и каждая группа из четырех бит задает десятичное число, равное сумме весов тех двоичных разрядов, значения которых равны 1.
Если w1, w2, w3, w4 – веса двоичных разрядов х1, х2, х3, х4, то десятичная цифра N = w1 ∙ х1 + w2 ∙ х2 + w3 ∙ х3 + w4 ∙ х4. Большинство десятичных счетчиков считают по взвешенному коду с весовыми коэффициентами 8-4-2-1.
Особыми свойствами взвешенных кодов обладают самодополняющийся код – это такой взвешенных код, у которого сумма любого число и другого числа, полученного из первого заменой нулей на единицы и единиц на нули равно 9. Код 8-4-2-1 несамодополяющийся. Существуют лишь 4 самодополняющихся кодов с положительными весами – (2-4-2-1), (3-3-2-1), (4-3-1-1), и (5-2-1-1). Нужно иметь в виду, что большинство чисел в самодополняющихся кодах можно представить несколькими способами.
5 = 4 + 1 = 0101,
5 = 2 + 2 + 1 = 1011
Самодополняющиеся коды получили распространение благодаря тому, что арифметическое устройство, обрабатывающее информацию в десятичном виде и работающее с этими кодами аппаратно проще.
Существует много невзвешенных двоичных кодов. Примером такого кода является код Джонсона, который реализуется с помощью одноименного счетчика.
Пятиразрядный счетчик Джонсона с модулем счета 10.
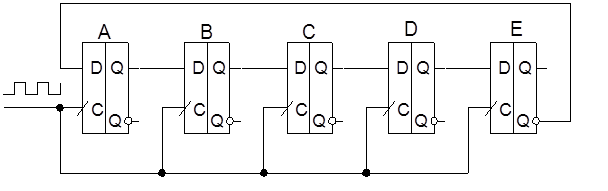Предположим, что все выходы триггеров установлены в
лог.0. Тогда таблица состояний будет:
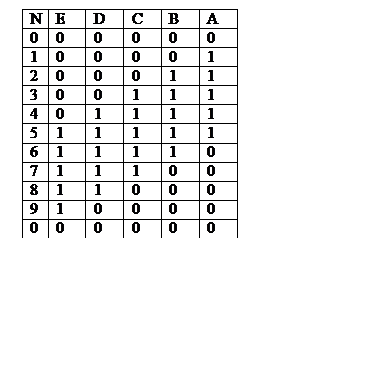Таблица
состояний счетчика Джонсона У счетчика Джонсона значительно
проще осуществляется кодирование, кроме того счетчики – делители легко сделать
с переменным коэффициентом деления. Модулем счета можно управлять, переключая
обратную связь. Если взять ее с D, то получится
делитель на 8, если с С то получится делитель на 6, т.е. Ксч = 2n. Счетчик с нечетным коэффициентом деления строится из
четного с Ксч = 2n устранением состояния
«все единицы» с помощью добавочных логических схем. Сигнал обратной связи при
этом равен для нечетных 
.
Нарисованная выше схема счетчика поясняет работу счетчика,
но она неполная: счетчик по такой схеме работает неустойчиво. При сбое в одном
из разрядов таблица состояний и модуль счета другие. Небольшое усложнение
позволяет избежать этого. Добавление основано на свойстве таблицы состояния
счетчика: 
К не взвешенным кодам относятся также циклические коды – такие коды, у которых последовательные кодовые наборы отличаются друг от друга лишь одним разрядом. Особенно важным среди циклических кодов является код Грея. Используя код Грея, можно проще построить некоторые типы АЦП. Эти коды также используются в ЭВМ, когда нужно управлять операциями, которые совершаются в строго определенной последовательности. При этом повышается надежность работы устройства, так как переход совершается только в одном разряде и проблема неодновременности переходов отпадает. Переход от кода Грея к двоичному коду можно осуществить с помощью логических схем. N-разрядный код Грея:
относится к классу рефлективных или отраженных кодов. Это значит, что n – разрядный код Грея получается отображением (n-1) разрядного. 4-х разрядный код Грея строится отражением 3-х разрядного относительно горизонтальной оси, расположенной ниже его таблицы. В старший разряд выше оси ставятся нули, а в младшие – единицы.
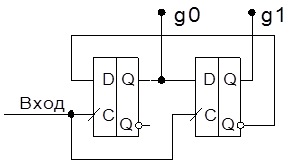
Ниже показан 2-х разрядный счетчик, который считает по
коду Грея . Рассматривая таблицу состояний 2-х разрядного кода Грея, можно увидеть:
, 
.
Строим счетчик с использованием D – триггеров.
2-ух разрядный счетчик по коду Грея.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.