Машиностроение \ Теория механизмов и машин

Анализ и синтез механизмов, страница 2

Сила полезного сопротивления прикладывается к ведомому звену и направляется противоположно скорости точки ее приложения.

Силовой расчет проводят по группам Ассура, так как они статически определимы. Начинаю расчет с группы Ассура, а заканчиваю ведущим звеном.

в) Рассматриваю равновесие группы Ассура и ведущего звена:

Рассмотрим группу Ассура 2-3.

Вычерчиваю в том же масштабе μl группу Ассура состоящую из звеньев 2-3.

Действие отброшенных звеньев 1 и 4 заменяю реакциями. Реакция в шарнире А неизвестна по направлению, разложу её на две составляющие: нормальную и касательную. Также поступлю с реакцией в шарнире С.

В центр масс S2 прикладываю вес G2, а в центр масс S3 прикладываю вес G3.

Под действием приложенных сил группа Ассура находится в равновесии, записываю уравнения равновесия группы:

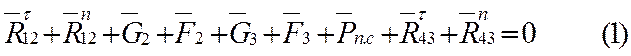
Определю реакцию  из уравнения моментов сил действующих на звено 2 относительно точки В:

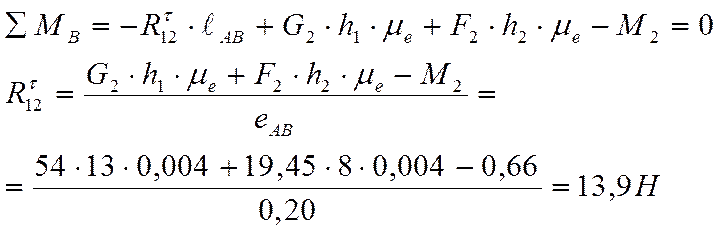
Определю реакцию  из уравнения моментов сил действующих на звено 3 относительно точки В:

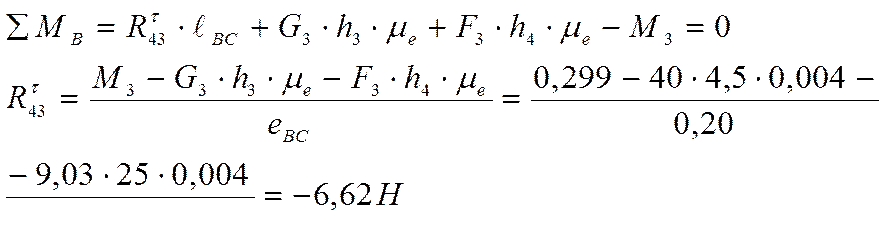
Реакции  и  найду графически построением плана сил. План сил строю на основе уравнения 1. Выбираю масштаб .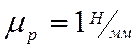

Из точки а провожу вектор  и откладываю отрезок  .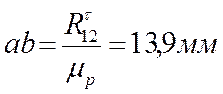

Из точки bпровожу линию действия веса G2 и откладываю отрезок .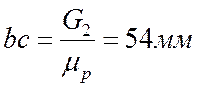

Из точки с провожу линию действия силы F2 и откладываю отрезок .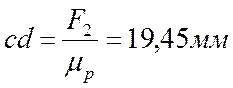

Из точки d провожу линию действия силы F3 и откладываю отрезок .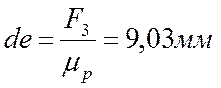

Из точки е провожу линию действия веса G3 и откладываю отрезок .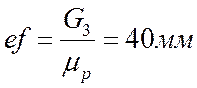

Из точки f провожу линию действия веса Рn.c. и откладываю отрезок .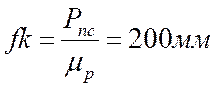

Из точки k провожу линию действия  и откладываю отрезок .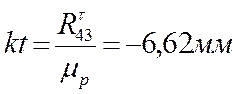

Тогда:

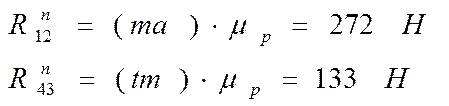
Соединив точку m с точкой b найду полную реакцию  действующую в шарнире а: .

Соединив точку k с точкой m найду полную реакцию  действующую в шарнире c: .

г) Рассмотрим равновесие ведущего звена 1.

Вычерчиваю звено 1 отдельно в масштабе μl.

Действие отброшенных звеньев заменю реакциями. В точке А

Реакция в шарнире О неизвестна по направлению, разложу её на составляющие (вдоль звена и перпендикулярно звену).

В центре масс S1 прикладываю вес G1 и силу инерции F1, она идет вдоль звена от центра вращения.

Так как ведущее звено не является группой Ассура (w=1), то чтобы уравновесить его прикладываю дополнительную так называемую уравновешивающую силу.

Прикладываю уравновешивающую силу к точке А кривошипа и направляю перпендикулярно звену.

Под действием сил ведущее звено находится в равновесии.

Записываю уравнение равновесия:

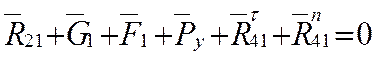
Силу  найду из уравнения моментов относительно точки О.

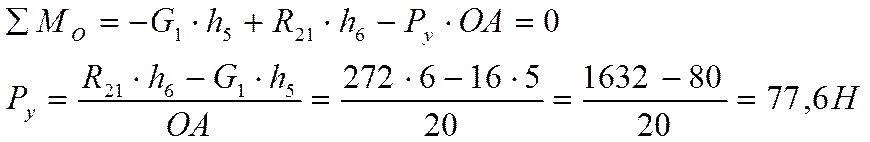
Для нахождения реакции в шарнире О  строю план сил.

План сил строю на основе уравнения равновесия. Выбираю масштаб .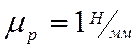

Из точки а провожу линию действия веса  и откладываю отрезок .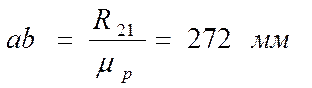

Из точки bпровожу линию действия веса G1 и откладываю отрезок .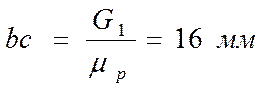

Из точки cпровожу линию действия веса F1 и откладываю отрезок .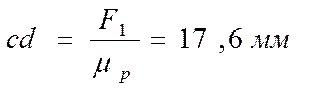

Из точки dпровожу линию действия веса Pу и откладываю отрезок .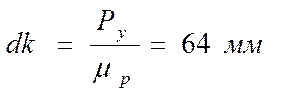

Соединив точку k с точкой а найду искомую реакцию в шарнире О.

Тогда .

д) Определение уравновешивающей силы методом жесткого рычага Жуковского.

Согласно теореме Жуковского поворачиваю план скоростей на 900 в любую сторону, например противоположно ω1, тогда рассматриваю его как жесткий рычаг, в соответствующие точки переношу силы, в точку а - Ру .

Моменты инерции представлю в виде сил:

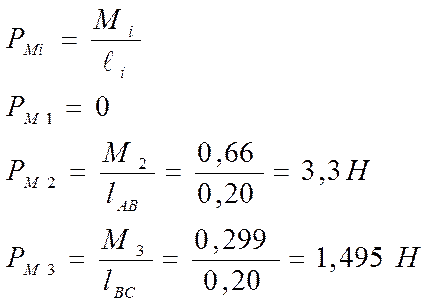
Рычаг Жуковского находится в равновесии, составляю уравнение моментов сил относительно полюса р:

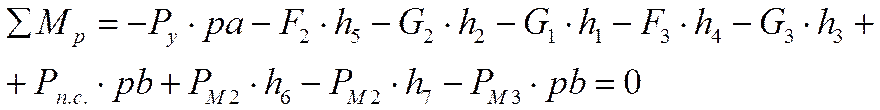
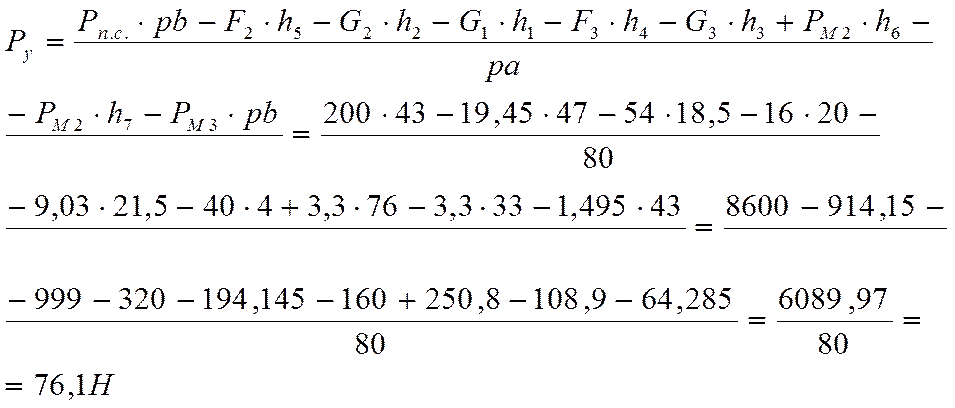
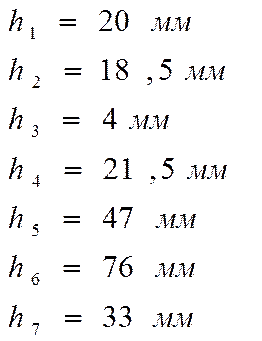
Сравнивая с результатом полученным ранее получаю отклонение:

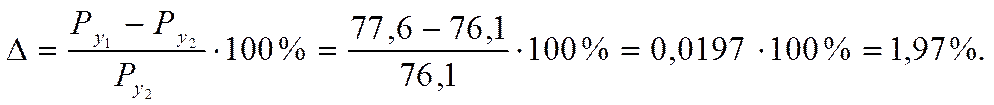
2. Планетарный механизм.

2.1 Подбор чисел зубьев по заданному передаточному отношению.

Данный зубчатый механизм состоит из двух ступеней: планетарной и простой. Поэтому передаточное отношение найду по формуле:

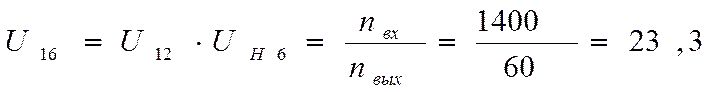
Принимаем, что 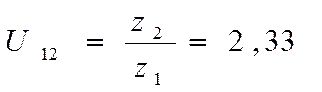, тогда

Принимая из условия отсутствия подреза ножек зубьев z1 = 18, тогда

Так как планетарная ступень является двухрядной с двумя внутренними зацеплениями, то для нахождения числа зубьев воспользуемся методом буквенных сомножителей.

Уравнение передаточного отношения:

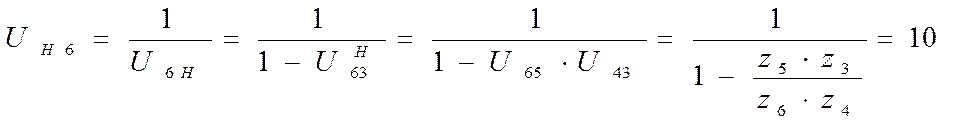, тогда

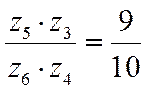
Условие соосности:  z3 + z4 = z6 + z5, или А + В = D + С

Перепишу уравнение передаточного отношения, используя буквенные сомножители:

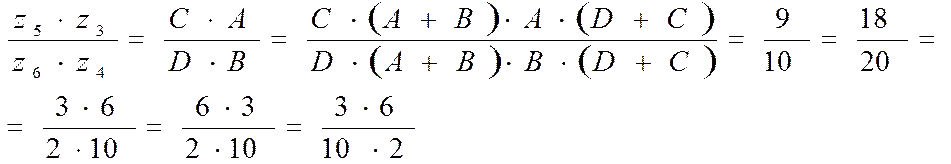
Подсчитаю числа зубьев для всех 3-х вариантов и выберу наиболее компактный вариант для дальнейшей проработки.

I

II

III

z3

6•(2 + 3) = 30

3•(2 + 6) = 24

6•(10 + 3)= 78

z4

10•(2 + 3) = 50

10•(2 + 6) = 80

2•(10 + 3)= 26

z5

3•(6 + 10) = 48

6•(3 + 10)= 78

3•(6 + 2)= 24

z6

2•(6 + 10) = 32

2•(3 + 10)= 26

10•(6 + 2)= 80

Наиболее компактный 1-ый вариант. Приму его для дальнейших вычислений. Проверю условия соседства и сборки.

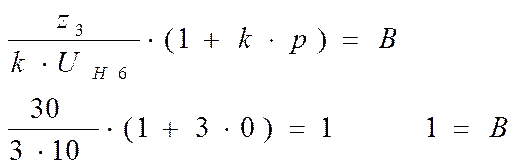Назначаю число сателлитов равное 3, т.е. k = 3, тогда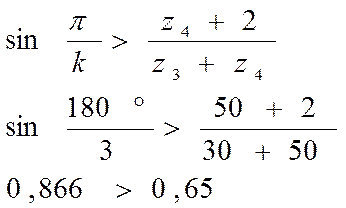

Условие сборки: 

Условия соседства и сборки выполняются.

2.2 Вычисление радиусов колес.

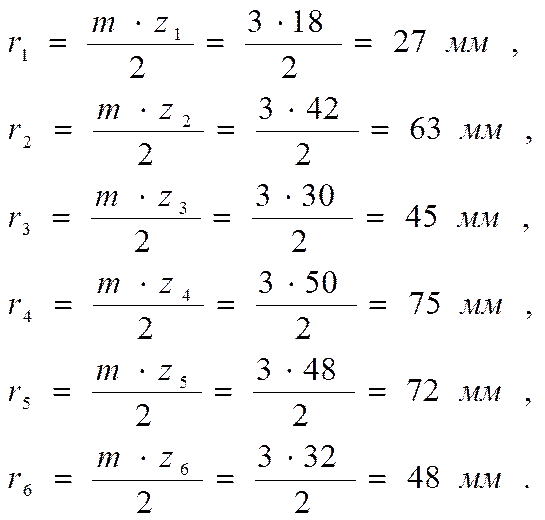
2.3 Построение схемы механизма.

Перпендикулярно построенной оси механизма отложим отрезок ОА произвольной длины 15 мм. тогда масштаб плана механизма будет равен:

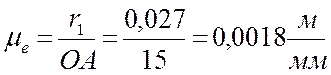
Тогда радиусы колес на плане будут равны:

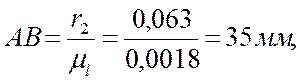
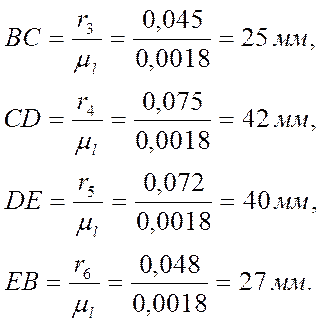
2.4 Аналитическое определение частот вращения.

1) 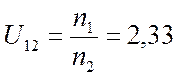, отсюда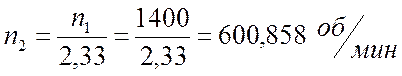

2)

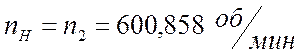
3) 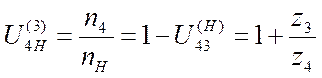, отсюда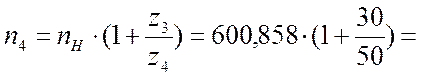

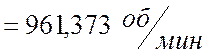
4)

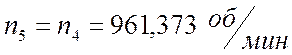
5) , так как колесо 3 неподвижно.

6)

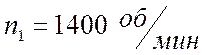
2.5 Построение плана линейных скоростей.

Проведем линию, перпендикулярную оси вращения колеса 1, на нее спроецируем характерные точки механизма: оси зубчатых колес и точки зацепления – О, А, В, С, D, Е.

Скорость точки О известна . Скорость точки А1 найду по формуле: .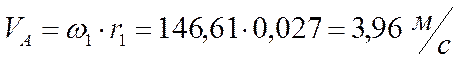

Отложим из точки А произвольный отрезок Аа = 60 мм. Тогда масштаб плана линейных скоростей будет равен:

.

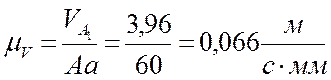Соединив точки а и О, получим треугольник распределения линейных скоростей точек колеса 1. (треугольник АаО).

Скорость точки В равна нулю, т.к. через нее проходит ось вращения колеса 2. Соединив точки а и В, получим треугольник распределения линейных скоростей точек колеса 2 (треугольник АаВ). Необходимо найти скорость точки D. Найдем её графически. Точка D принадлежит водилу H, поэтому спроецируем ее на линию аВ, получу точку d. Соединяем точки d и B, полученный треугольник DdВ – треугольник распределения линейных скоростей точек водила Н.

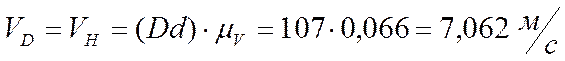
Скорость точки С равна нулю, т.к. эта точка – МЦС (мгновенный центр скоростей). Соединим точки d и С. Треугольник DdС – треугольник распределения линейных скоростей сателлитов 4 и 5. Необходимо найти скорость точки Е. Точка Е принадлежит сателлитам 4 и 5, поэтому спроецирую ее на линию Сd, получу точку е. Соединяю точки Е, е и В. Полученный треугольник ЕеВ – треугольник распределения линейных скоростей точек колеса 6.

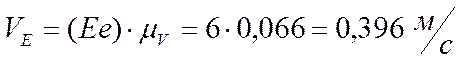
2.6 Построение плана чисел оборотов.

Построим горизонтальную прямую х. От нее перпендикулярно вниз отложи произвольный отрезок kp = 30 мм. Тогда масштаб плана чисел оборотов будет равен:

.

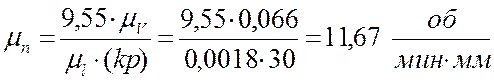В точку р параллельно самим себе перенесу все наклонные линии с плана линейных скоростей. На пересечении этих линий с прямой х получаю точки 1;

2,Н; 4,5; 6. Теперь можем определить частоты вращения звеньев:

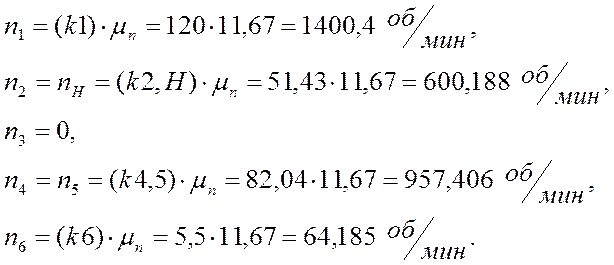
Сравнивая значения частот вращения, полученных аналитическим и графическим методами, можем сделать вывод: погрешность расчета мала.

Список используемой литературы:

1 Артоболевский, И. И. Теория механизмов и машин / И. И. Артоболевский. – М.: Наука, 1975. – 640 с.

2 Артоболевский, И. И. Сборник задач по теории механизмов и машин / И. И. Артоболевский, Б. В. Эдельштейн. – М.: Наука, 1987. – 256 с.

Скачать файл